💡 백준 11653
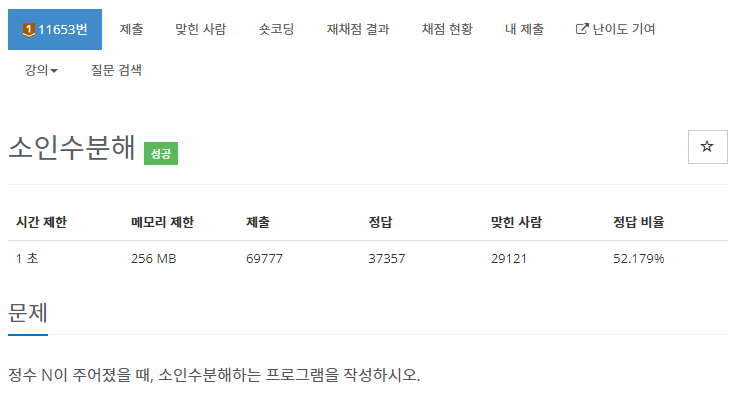
◽ 문제
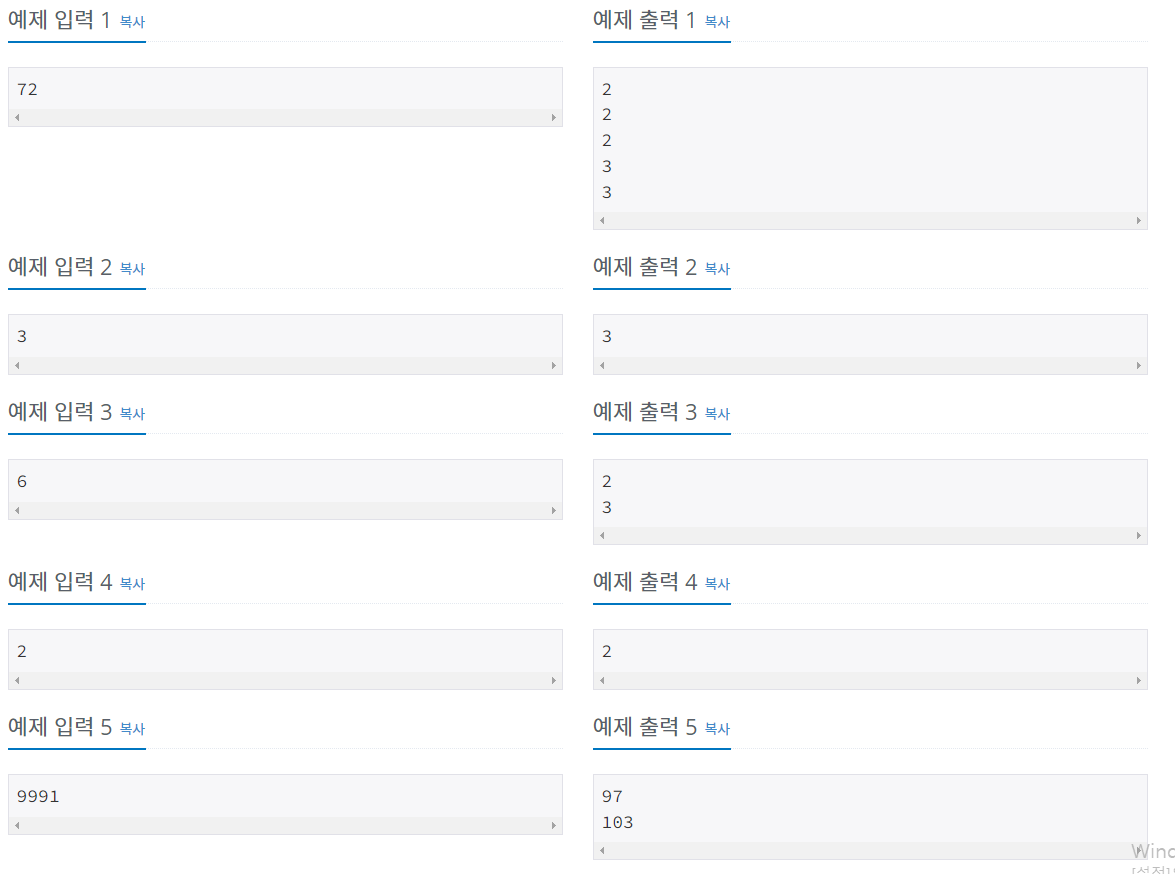
◽ 입력 & 출력

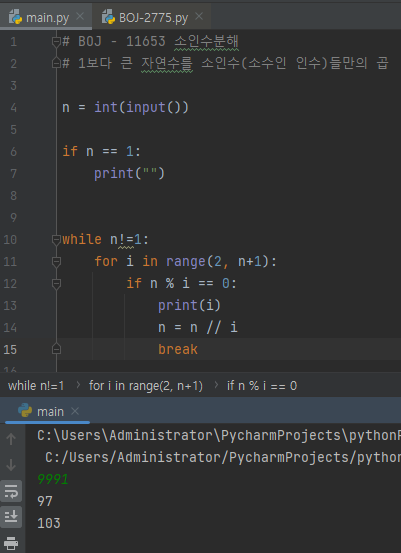
◽ 풀이
- 정수 N이 주어졌을 때, 소인수분해하는 프로그램을 작성하는 문제이다.
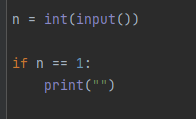
- 정수 n을 입력받고 1일경우
아무것도 출력하지 않는다.
-
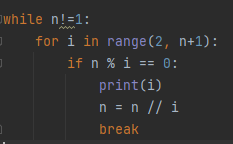
정수 n이 1이 아닐때만 반복문을 돈다.
-
for문에서는 2에서 n+1까지 범위
-
i(2부터 시작)으로 나눠질 때까지(N % m == 0) 나눈다.
-
나눈 값(소수)을 출력한다.
💡 배운점

- 시간이 오래걸려서 시간단축을 위해 다른 풀이를 참고해보았다.
✅성공코드
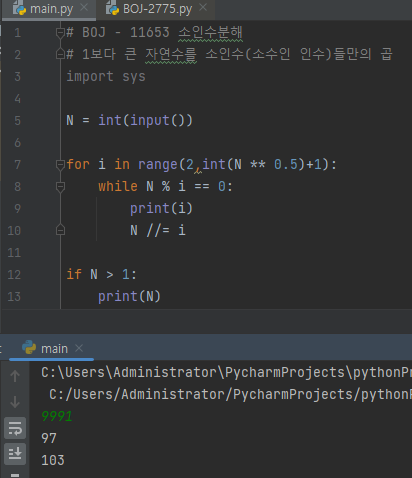

- 속도가 몇십배는 빨라졌다.
◽ 범위 줄이기
-
위의 코드가 속도가 빠른 이유는 반복 횟수를 제곱근만큼 줄였기 때문이다.
-
ex)9991
-
9991은 97과 103 두 수로 소인수분해가 된다.
-
이 값이 나오기까지 a는 2부터 97까지 계속해서 a += 1을 반복하고 (여기까지는 모든 코드가 동일)
-
그다음 103이 나올 때까지 또 a += 1을 반복한다.
-
하지만 세 번째 코드의 경우 입력받은 값의 루트만큼 반복문을 돌려서 반복 횟수를 대폭 줄였다.
-
√9991 = 99.9549...

-
이므로 99까지만 계산하면 되며 남은 숫자가 1이 아니면 가장 마지막에 나와서 print(n)을 해주어 남은 소인수분해 값을 출력해준다.
-
위와 같은 방법으로 기존 첫 번째와 두 번째 코드처럼
끝까지 값을 찾아서 나눠주는 게 아닌 -
적당히 찾아서 나눠주는 방식으로 반복문 횟수를 대폭 줄여 빠른 실행시간을 얻었다.
소인수 분해를 하는 것이기 때문에, 어떤 수 N을 나누는 수는 제곱근 이상으로 값이 필요하지 않기 때문에 제곱근을 하여 i의 범위를 지정한 것이다
출처: https://baby-dev.tistory.com/95 [애기 개발자:티스토리]
