백준 18870 - 좌표 압축(파이썬)

💡백준 18870 - 좌표 압축

◽ 문제

---

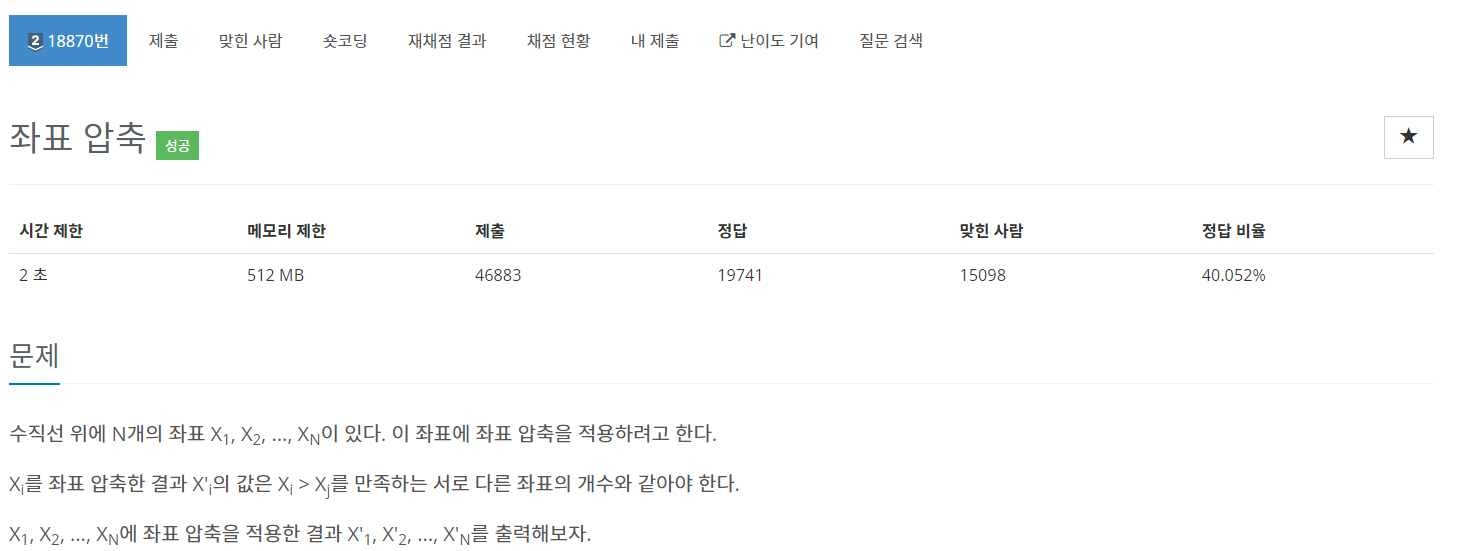
◽ 입력 & 출력 & 제한

---

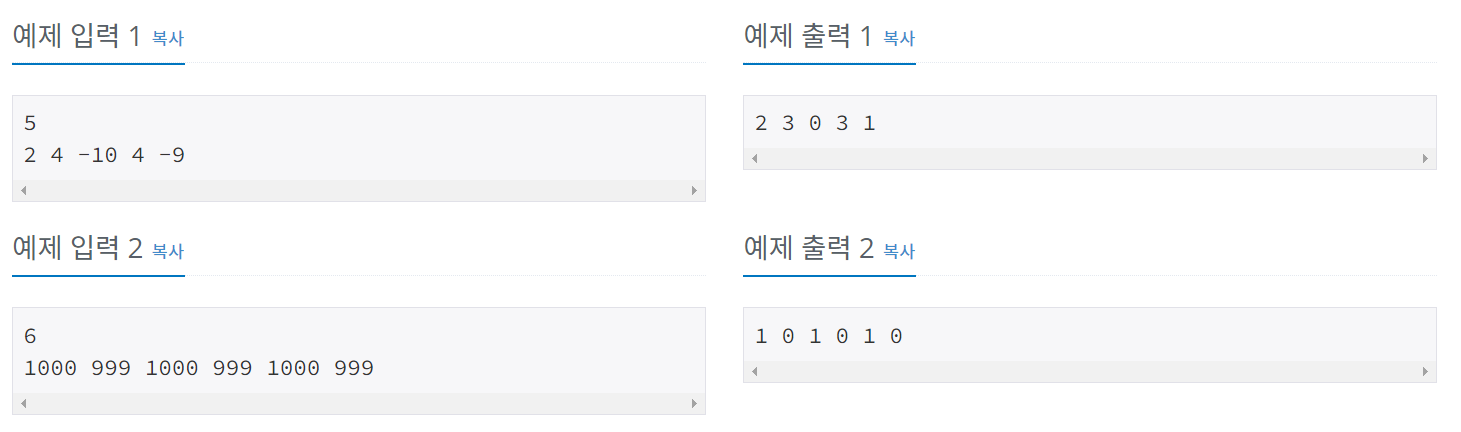
◽ 풀이

1 ≤ N ≤ 1,000,000 좌표값에 있는 좌표들 중 입력받은 일부 좌표들을 모아서 압축하여 순서대로 표현해야한다.

• list.index(i)의 형태는 시간복잡도 O(N) ➡️ 매번 최대 1,000,000번의 수행이 되면서 시간초과

• { dict[요소] : 요소의 index } 의 형태 시간 복잡도 O[1] ➡️ 매번 최대 입력 수 만큼 수행

✅ 요약

• 입력받은 좌표를 크기순으로 정렬 하여 순서를 출력

• 즉, 작은 값부터 시작해서 0부터 인덱스를 부여

• 시간복잡도 주의

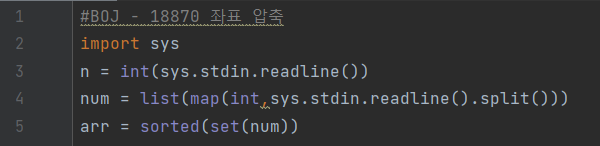
• 3번째 줄: 좌표의 개수를 입력받는다.

• 4번째 줄: 좌표를 공백을 기준으로 분리하여 리스트형식으로 입력받는다.

• 5번째 줄: 입력받은 좌표들을 중복을 제거하기 위해서 set형으로 바꿔준다.

• 출력 결과

---

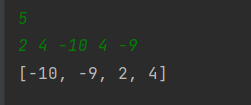
• 9번째 줄: arr의 길이(0~3)를 arr배열의 요소에 넣어준다.
  ➡️ 즉 arr(키)에 0,1,2,3(값)을 넣어줌.

arr[0] = -10 , arr[1] = -9 , arr[2] = 2 , arr[3] = 4 에다가 0,1,2,3을 넣어준다.

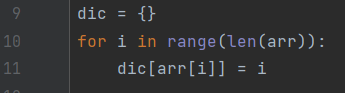
위 두개의 코드는 같은 코드입니다.

• 출력 결과
  

---

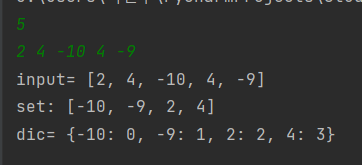
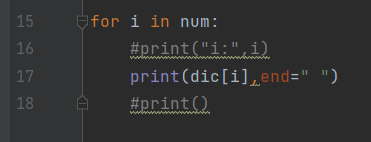
• 15번째 줄 for문: 딕셔너리 dic인 키에 input에 해당하는 값을 출력한다.
  
  
  
• 출력 결과

---

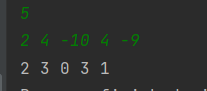
✅ 전체 코드

---

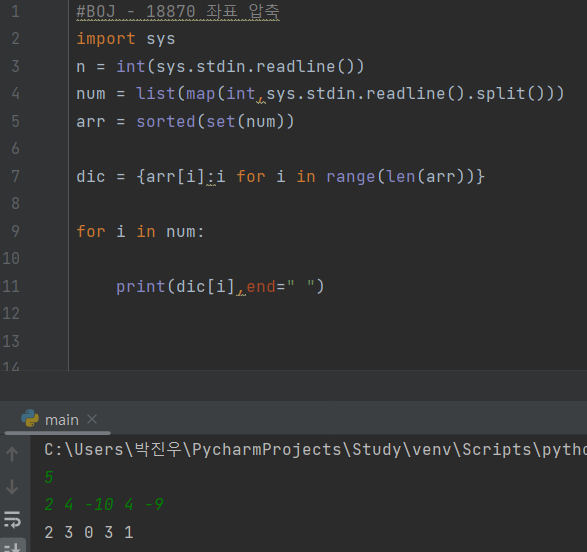
💡배운점

◽ 딕셔너리

• 딕셔너리는 중괄호 { }로 선언하며, '키: 값'형태 를 쉼표( , )로 연결해서 만든다.

• 데이터 추가

  대괄호([키] = 값)를 사용하여 원하는 값을 할당

• 데이터 삭제

  del 키워드를 사용해서 특정 키와 값의 쌍을 사전에서 제거

• 특정 키 존재 확인
  
  
  
  

---

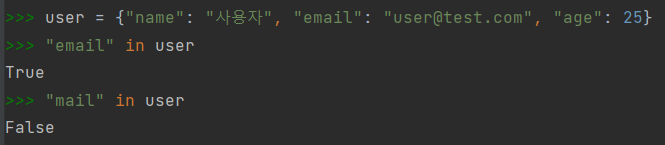
◽ 리스트 시간복잡도

연산	시간 복잡도	설명
len(a)	$O(1)O(1)O(1)$	전체 요소의 개수를 리턴한다.
a[i]	$O(1)O(1)O(1)$	인덱스 $iii$의 요소를 가져온다.
a[i:j]	$O(k)O(k)O(k)$	$iii$부터 $jjj$까지 슬라이스의 길이만큼 $kkk$개의 요소를 가져온다. 이 경우 객체 $kkk$개에 대한 조회가 필요하므로 $O(k)O(k)O(k)$이다.
elem in a	$O(n)O(n)O(n)$	elem 요소가 존재하는지 확인한다. 처음부터 순차 탐색하므로 $nnn$만큼 시간이 소요된다.
a.count(elem)	$O(n)O(n)O(n)$	elem 요소의 개수를 리턴한다.
a.index(elem)	$O(n)O(n)O(n)$	elem 요소의 인덱스를 리턴한다.
a.append(elem)	$O(1)O(1)O(1)$	리스트 마지막에 elem 요소를 추가한다.
a.pop()	$O(1)O(1)O(1)$	리스트 마지막 요소를 추출한다. 스택의 연산이다.
a.pop(0)	$O(n)O(n)O(n)$	리스트 첫번째 요소를 추출한다. 큐의 연산이다. 이 경우 전체 복사가 필요하므로 $O(n)O(n)O(n)$이다.
del a[i]	$O(n)O(n)O(n)$	i에 따라 다르다. 최악의 경우 $O(n)O(n)O(n)$이다.
a.sort()	$O(nlogn)O(nlogn)O(nlogn)$	정렬한다. 팀소트(Timsort)를 사용하며, 최선의 경우 $O(n)O(n)O(n)$에도 실행될 수 있다.
min(a), max(a)	$O(n)O(n)O(n)$	최솟값/최댓값을 계산하기 위해서는 전체를 선형탐색해야 한다.
a.reverse()	$O(n)O(n)O(n)$	뒤집는다. 리스트는 입력 순서가 유지되므로 뒤집게 되면 입력 순서가 반대로 된다.

---

◽ 딕셔너리 시간복잡도

연산	시간 복잡도	설명
len(a)	$O(1)O(1)O(1)$	요소의 개수를 리턴한다.
a[key]	$O(1)O(1)O(1)$	키를 조회하여 값을 리턴한다.
a[key] = value	$O(1)O(1)O(1)$	키/값을 삽입한다.
key in a	$O(1)O(1)O(1)$	딕셔너리에 키가 존재하는지 확인한다