이진트리

이전에 트리에 대해서 그래프와 함께 정리해둔 포스트가 있다. 트리와 이진트리의 확실한 차이점은 이진트리는 최대 2개의 자식을 가지고 트리는 개수의 제한이 없다. 또한 이진트리는 각각의 자식노드는 자신이 부모의 왼쪽인지 오른쪽 자식인지 지정된다.

트리의 성질 : 노드가 N개인 트리는 항상 N-1개의 엣지를 가진다.

목적

이진트리의 사용목적은 효율적인 탐색을 위해 사용한다.
이진 트리는 자료의 삽입,삭제 방법에 따라 3가지로 나뉜다.
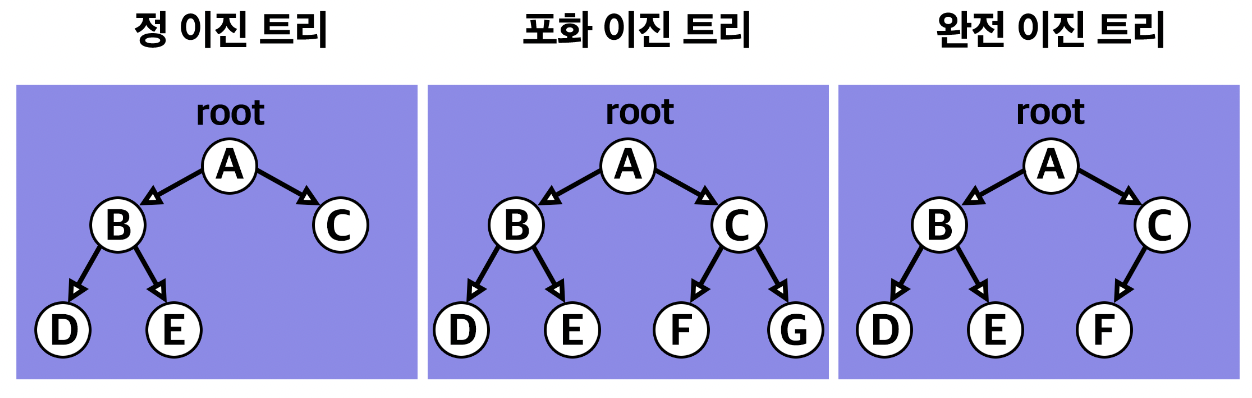
1. 정 이진 트리(Full binary tree) : 각 노드가 0개 혹은 2개의 자식 노드를 갖는다.
2. 완전 이진 트리(Complete binary tree) : 마지막 레벨을 제외한 모든 노드가 가득 차 있어야하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만, 왼쪽이 채워져있어야한다.
3. 포화 이진 트리(perfect binary tree) : 정 이진 트리이면서 완전 이진트리인 경우이다. 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 체워져있어야한다.

이진탐색 트리의 한계

이진 탐색 트리는 균형 잡힌 트리가 아닐때, 입력되는 값으 순서에 따라 한쪽으로 노드들이 몰리게 될 수 있다.
균형이 잡히지 않은 트리는 탐색하는 데 시간이 더 걸리는 경우도 있어서 항상 생각하고 해결해주어야한다.

트리 순회

특정 목적을 위해 트리의 모든 노드를 한 번씩 방문하는 것을 트리 순회라고 한다.

전위 순회(preorder traverse)

부모노드를 탐색후 왼쪽 자식 노드를 탐색한다. 그뒤 오른쪽 자식 노드를 탐색한다.
만약 왼쪽 노드에 자식 노드가 또 있을경우 위행동을 반복한다. (재귀를 사용하여 탐색가능)

중위 순회(inorder traverse)

왼쪽 자식노드를 확인후 부모노드를 확인한다. 그뒤 오른쪽 자식 노드를 확인한다.

후위 순회

왼쪽 자식 노드를 확인후 오른쪽 자식 노드를 확인한다. 그뒤 부모노드를 확인한다.