트리의 지름 구하기

트리의 지름 구하기

트리에서 지름이란, 가장 먼 두 정점 사이의 거리 혹은 가장 먼 두 정점을 연결하는 경로를 의미한다. 선형 시간안에 트리에서 지름을 구하는 방법은 다음과 같다

1. 트리에서 임의의 정점 x를 잡는다.
2. 정점 x에서 가장 먼 정점 y를 찾는다.
3. 정점 y에서 가장 먼 정점 z를 찾는다.

트리의 지름은 정점 y와 정점 z를 연결하는 경로다.

증명) 트리에서 정점 u와 정점 v를 연결하는 경로가 트리의 지름이라고 가정하자. 임의의 정점 x를 정하고, 정점 x에서 가장 먼 정점 y를 찾았을 때, 아래와 같이 경우를 나눌 수 있다.

i. x가 u 혹은 v인 경우
ii. y가 u 혹은 v인 경우
iii. x, y, u, v가 서로 다른 경우


자명하게 i., ii.에 대해서 위 알고리즘이 트리의 지름을 올바르게 구한다는 것을 알 수 있다. -> (당연함)

이제 iii. 경우에 대해서 알고리즘이 트리의 지름을 올바르게 구한다는 것을 증명하면 된다.

iii. 경우일 때 아래와 같이 두 가지 경우가 가능하다.

a. 정점 x와 정점 y를 연결하는 경로가 정점 u와 정점 v를 연결하는 경로와 한 점 이상 공유하는 경우
b. 정점 x와 정점 y를 연결하는 경로가 정점 u와 정점 v를 연결하는 경로와 완전히 독립인 경우

d(s,t)를 트리에서 정점 s와 정점 t의 거리라고 하자. 

iii-a.

정점 x와 정점 y를 연결하는 경로가 정점 u와 정점 v를 연결하는 경로와 한 점 이상 공유하는 경우

아래 그림에서 d(t,y)=max(d(t,u),d(t,v))라는 것을 알 수 있다. 때문에 위 알고리즘은 트리의 지름을 올바르게 구한다.

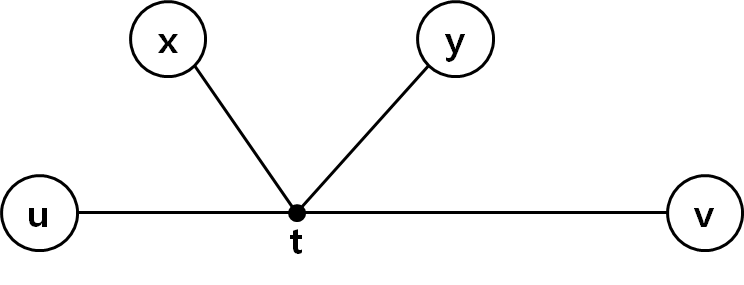
• 트리의 지름은 d(u,v)
• 임의의 정점 x에서 가장 먼 것은 y
• d(t,y) 는 d(t,u) 또는 d(t,v) 이다.
  왜냐하면 x에서 제일 먼 거리는 y이고
  u,v는 트리의 지름이기 때문에 t에서 더 먼 정점 max(d(t,u),d(t,v)) 이 y가 된다.
• x에서 t를 거쳐서 트리의 지름의 끝점으로 가야됨

  • t에서 가장 거리가 먼 점으로 가야한다.

  • d(x,y) 경로에서는 t에서 가장 먼 점이 y

  • d(u,v) 경로에서는 t에서 가장 먼 점이 u or v

  • 그래서 y 는 u or v 이다.

    
    

iii-b.

정점 x와 정점 y를 연결하는 경로가 정점 u와 정점 v를 연결하는 경로와 완전히 독립인 경우

아래 그림과 같은 상황이 된다는 것인데 u에서 제일 먼 점이 v가 아니라 y가 되어 u와 v를 연결하는 경로가 트리의 지름이 된다는 가정에 모순된다. 때문에 b.의 경우는 불가능하다는 것을 알 수 있다.

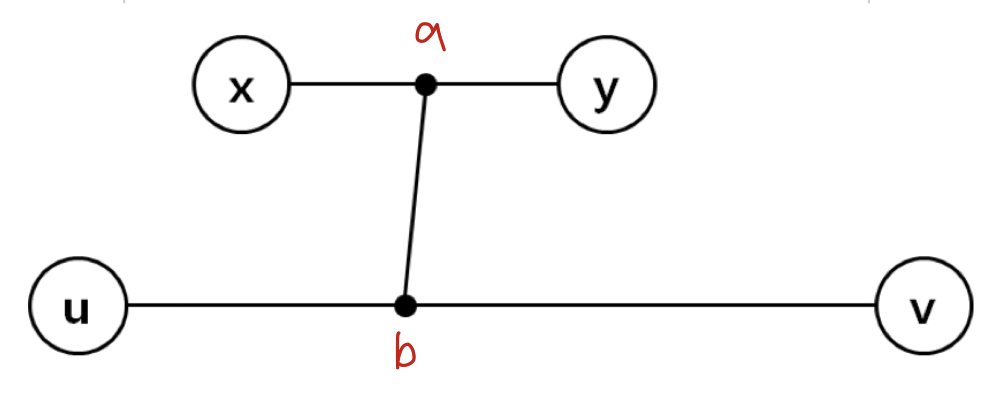
d(x,y) 입장에서

d(a,y) > d(a,b,v)

• d(a,y) 의 길이가 더 길어야 한다.

• x에서 가장 먼 정점이 y 이기 때문

d(u,v) 입장에서

d(b,v) > d(b,a,y)

• d(b,v) 의 길이가 더 길어야 한다.

• u와 v 가 트리의 지름이기 때문 ( u에서 가장 먼 정점 : v )

서로 자기가 더 길다고 하기 때문에 모순이다.

1) d(a,y) > d(a,b,v)
2) d(b,v) > d(b,a,y)

2)번의 d(b,v) 를 1)번 식에 대입하면
d(a,y) > d(a,b,v) > d(b,a,y)
다음과 같은 식이 나오는데 d(a,y) > d(b,a,y)는 불가능하므로 모순이 된다.

그래서 iii 인 경우에는 d(x,y) 와 d(u,v)가 한 점 이상을 공유할 수 밖에 없다.

결론

i, ii, iii-a case가 성립하고 iii-b case가 모순이므로
트리의 지름을 구하는 방법은 아래와 같이 구할 수 있다.

1. 트리에서 임의의 정점 x를 잡는다.
2. 정점 x에서 가장 먼 정점 y를 찾는다.
3. 정점 y에서 가장 먼 정점 z를 찾는다.

트리의 지름은 정점 y와 정점 z를 연결하는 경로다.

출처 https://blog.myungwoo.kr/112