DP를 풀면서 느낀점
문제를 풀어나가는 규칙을 찾아야 하는데
규칙을 찾는 과정에서 재귀적 사고를 해야하고
큰 문제를 작은 부분문제로 나눌 수 있어야한다.
그리고 작은 부분 문제에서 어떤 값을 저장해놨다가
다음 단계의 문제를 풀 때 불러서 써야할지 생각해야한다.
DP 테이블에 초기값을 저장하기 위해 낮은 단계는 직접
경우의 수를 대입해보면 좋다.
증가 부분 수열
원소가 n개인 배열의 일부 원소를 골라내서 만든 부분 수열 중, 각 원소가 이전 원소보다 크다는 조건을 만족
n = 1000이며, 시간 제한이 1초이므로 대략 O(n^2)시간의 알고리즘을 설계하면 해결할 수 있는 문제다
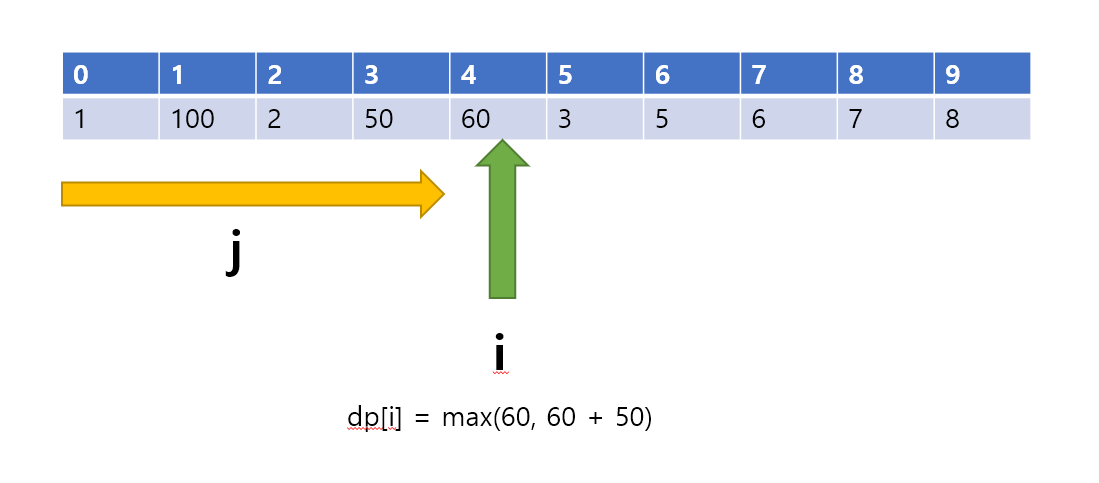
예를 들어,
수열 A = {1, 100, 2, 50, 60, 3, 5, 6, 7, 8} 인 경우에 합이 가장 큰 증가 부분 수열은
A = {1, 100,2,50,60, 3, 5, 6, 7, 8} 이고, 합은 113이다.
어려웠던 점
dp[i] = max(dp[i],number[i] + dp[j]) 이 코드에서 dp[i]가 더 큰 경우도 있는 걸까 ?
다음으로 if문을 사용하여 현재 수열이 증가하고 있는 지를 확인 한 후, 수열이 증가하고 있다면 현재 대상 값보다 이전까지의 합 + 현재 값이 더 큰지 확인한다. 이 둘 모두가 성립할 경우, 이전까지의 합과 현재 값을 더해 현재 비교 대상 값에 넣어준다.
이를 반복하게 되면 증가하는 수열의 합을 구할 수 있다.
예시를 보고 이해
{1, 10, 2, 5, 20}이런 수열이 있을 때,
0에서 출발한다. 자기자신이므로 합은 1이다.
--> dp[0] = 1
10에 도착했다. 10>1을 만족하므로 합은 11이다.
--> dp[1] = 11
2에 도착했다. 2와 앞의 원소를 하나씩다 비교하여 최댓값을 골라낸다.
2>1을 만족하므로 합은 dp[0]+2 = 3
--> dp[2] = 3
5에 도착했다. 5와 앞의 원소를 하나씩 다 비교하여 최댓값을 골라낸다.
5>1을 만족하므로 합은 dp[0]+5 = 6
5>2을 만족하므로 합은 dp[2]+5 = 8
둘중 큰 값은 8이다.
--> dp[3] = 8
20에 도착했다. 20과 앞의 원소를 하나씩 다 비교하여 최댓값을 골라낸다.
20>1을 만족하므로 합은 dp[0]+20 = 21
20>10을 만족하므로 합은 dp[1]+20 = 31
20>2을 만족하므로 합은 dp[2]+20 = 23
20>5를 만족하므로 합은 dp[3]+20 = 28
넷중 큰 값은 31이다.
--> dp[4] = 31
dp의 값을 나열해보면 다음과 같다.
1, 11, 3, 8, 31
따라서 가장 큰 값을 골라내면 답은 31이다
코드
A = input()
number = list(map(int,input().split()))
dp = number[:]
for i in range(len(number)):
for j in range(i):
if number[i] > number[j] :
dp[i] = max(dp[i],number[i] + dp[j])
print(max(dp))
