[Algorithm] 데이크스트라 알고리즘

---

1 - Dijkstra Algorithm 이란?

그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘.

데이크스트라 알고리즘은 두 꼭짓점 간의 가장 짧은 경로를 찾는 알고리즘이지만, 일반적인 변형은 한 꼭짓점을 기준으로하여 그래프의 다른 모든 꼭짓점까지의 최단 경로 트리를 만드는 것이다.

음이 아닌 가중치를 가지는 무작위 유향 그래프에서의 단일 소스 최단 경로 알고리즘 중 점근적으로 가장 빠른 알고리즘이다.

---

2 - 시간 복잡도

원래의 데이크스트라 알고리즘은 $O(|V|^2)$ 의 시간복잡도를 가진다.

우선순위 큐를 기반으로 하는 데이크스트라의 경우 각 노드마다 미방문 노드 중 출발점으로부터 현재까지 계산된 최단 거리를 가지는 노드를 찾는데 $O(|V|log|V|)$의 시간이 필요하고, 각 노드마다 이웃한 노드의 최단 거리를 갱신할 때 $O(|E|log|V|)$의 시간이 필요하기 때문에 $O(|E| + |V|log|V|)$ 의 시간복잡도를 가진다.

• $V$ : Vertex (정점의 개수)
• $E$ : Edge (간선의 개수)

---

3 - 동작 방식

1. 출발점으로부터의 최단거리를 저장할 배열 $d[V]$ 를 만들고, 출발 노드에는 0을, 출발점을 제외한 다른 노드들에는 매우 큰 값 INF를 채워 넣는다. (무한으로 간주될 수 있는 값을 의미함.)

2. 현재 노드를 나타내는 변수 $X$ 에 출발 노드의 번호를 저장한다.

3. $X$ 로부터 갈 수 있는 임의의 노드 Y에 대해, $d[X]$ 에 두 정점 사이의 거리를 더한 값과 $d[Y]$ 의 값을 비교한다. (INF와 비교할 경우 무조건 전자가 작다.)

4. 만약 $d[X]$ + 두 정점 사이의 거리의 값이 더 작다면, 즉 더 짧은 경로라면, $d[Y]$의 값을 이 값으로 갱신시킨다.

5. $X$ 의 모든 이웃 노드 $Y$ 에 대해 이 작업을 수행한다.

6. $X$ 의 상태를 방문 완료로 바꾼다. 그러면 이제 더 이상 $X$ 는 사용하지 않는다.

7. 미방문 상태인 모든 노드들 중, 출발점으로부터의 거리가 제일 짧은 노드 하나를 골라서 그 노드를 $X$ 에 저장한다.

8. 도착 노드가 방문 완료 상태가 되거나, 혹은 더 이상 미방문 상태의 노드를 선택할 수 없을 때까지, 3~7의 과정을 반복한다.

9. 이 작업을 마친 뒤, 도착 노드에 저장된 값이 바로 $X$ 로부터의 최단 거리이다. 만약 이 값이 INF라면, 중간에 길이 끊긴 것임을 의미한다.

---

4 - 동작 예시

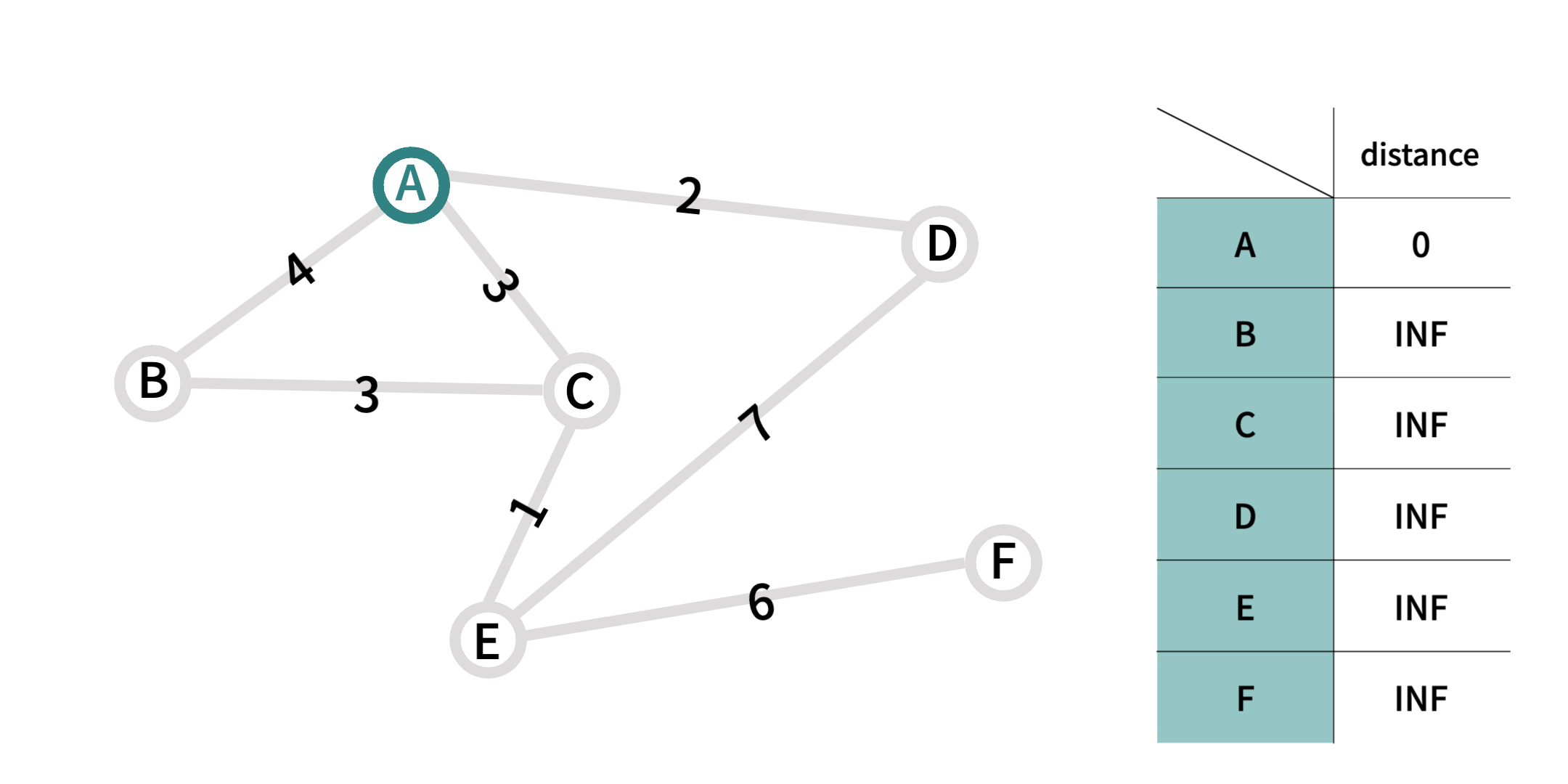
• A 지점에서 시작하여 F 지점에 도달하기 위한 최단경로를 찾는다.
• A 지점 은 시작점이므로 distance = 0, 다른 지점들은 INF 값을 갖는다.

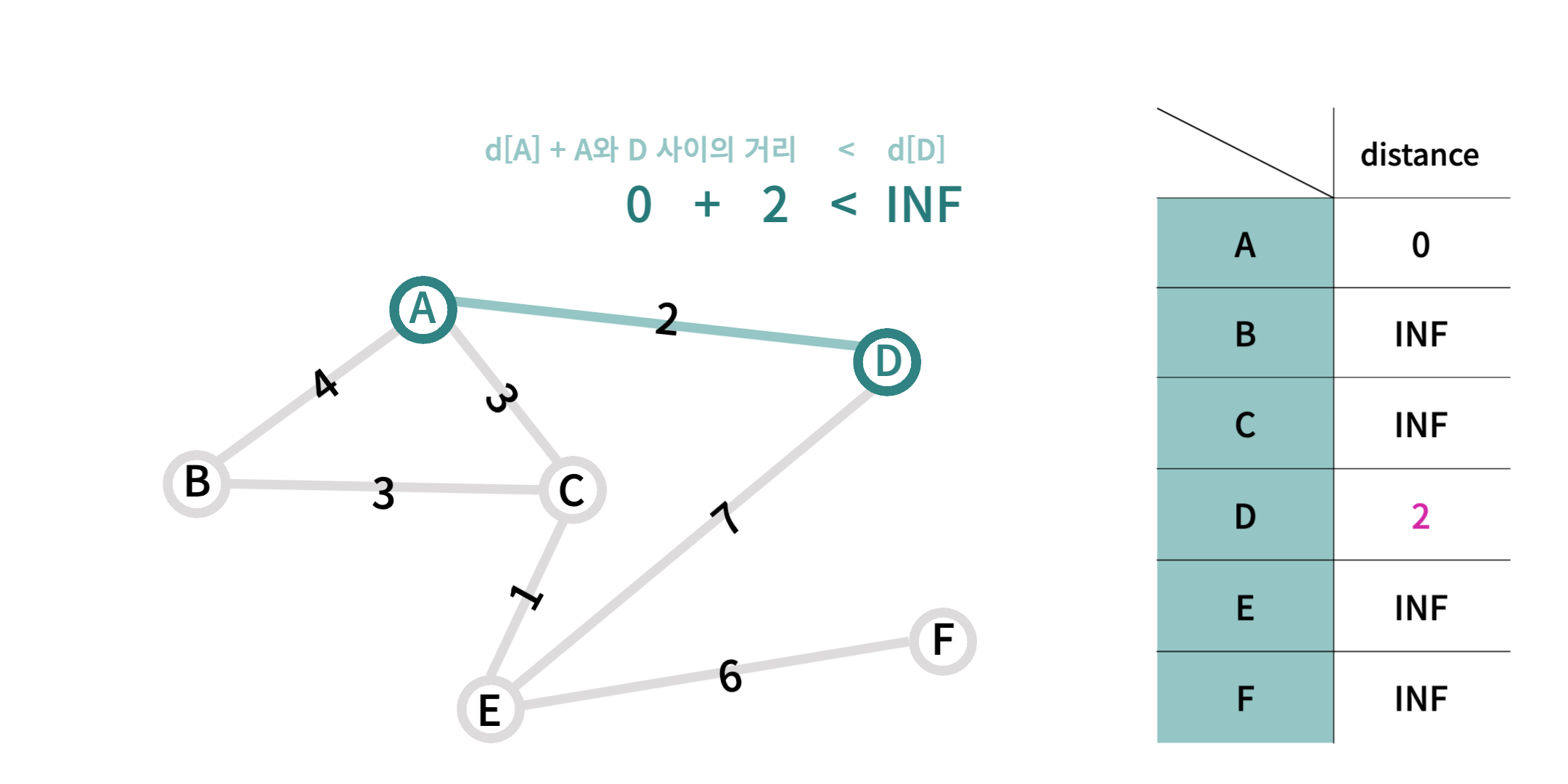
• 출발 노드 A 지점의 이웃 노드 중 하나인 D 지점 까지의 거리는 d[A] + 두 지점 사이의 거리 의 값이 기존값 d[D] 보다 작으므로 새로운 값 2 로 갱신된다.

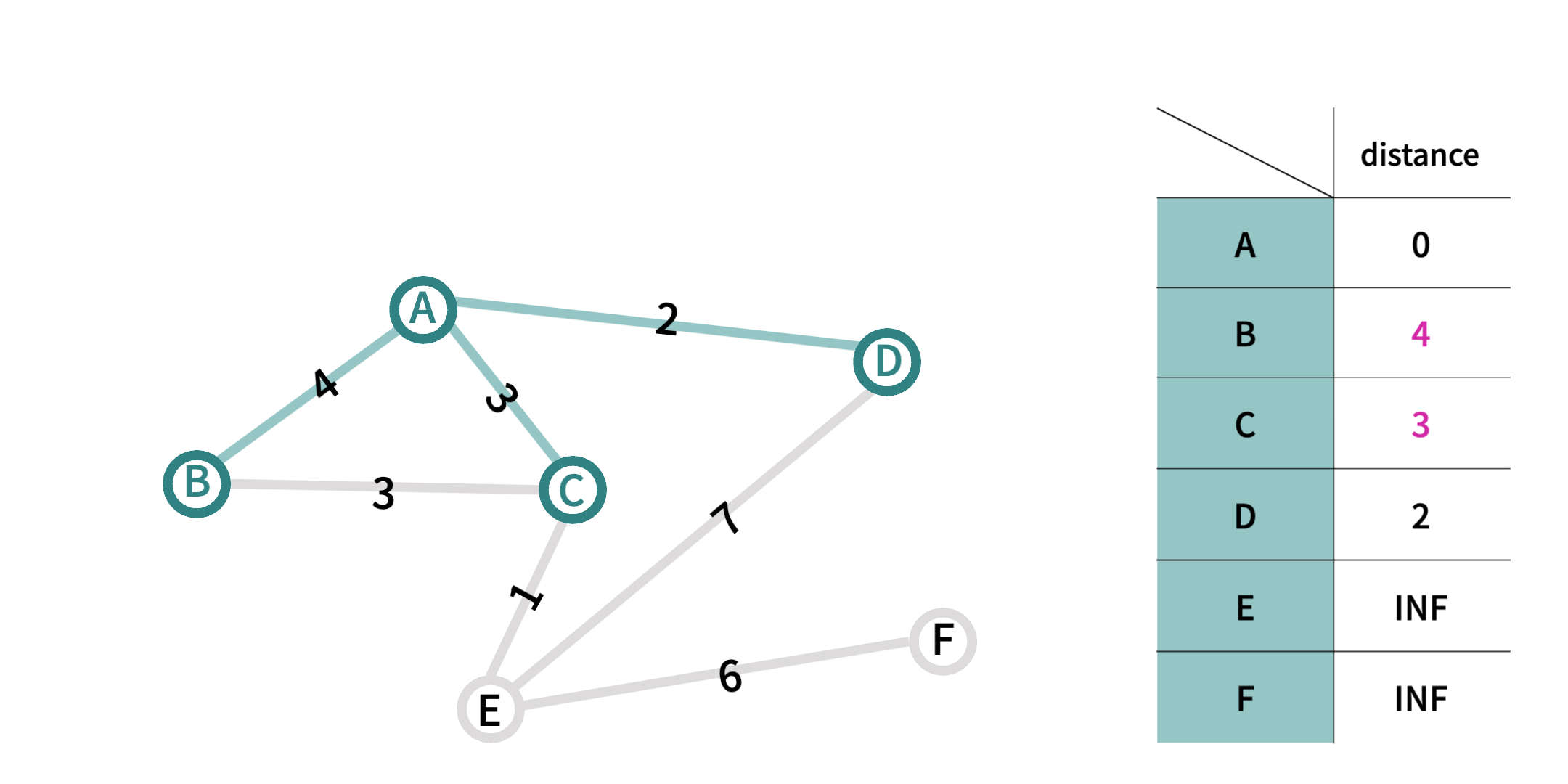
• 같은 방식으로 A 지점 의 이웃 노드 B 지점 과 C 지점 도 값을 갱신한다.
• A 지점 은 모든 이웃 노드를 방문하였으므로 더이상 사용하지 않는다. ( 방문 완료 )

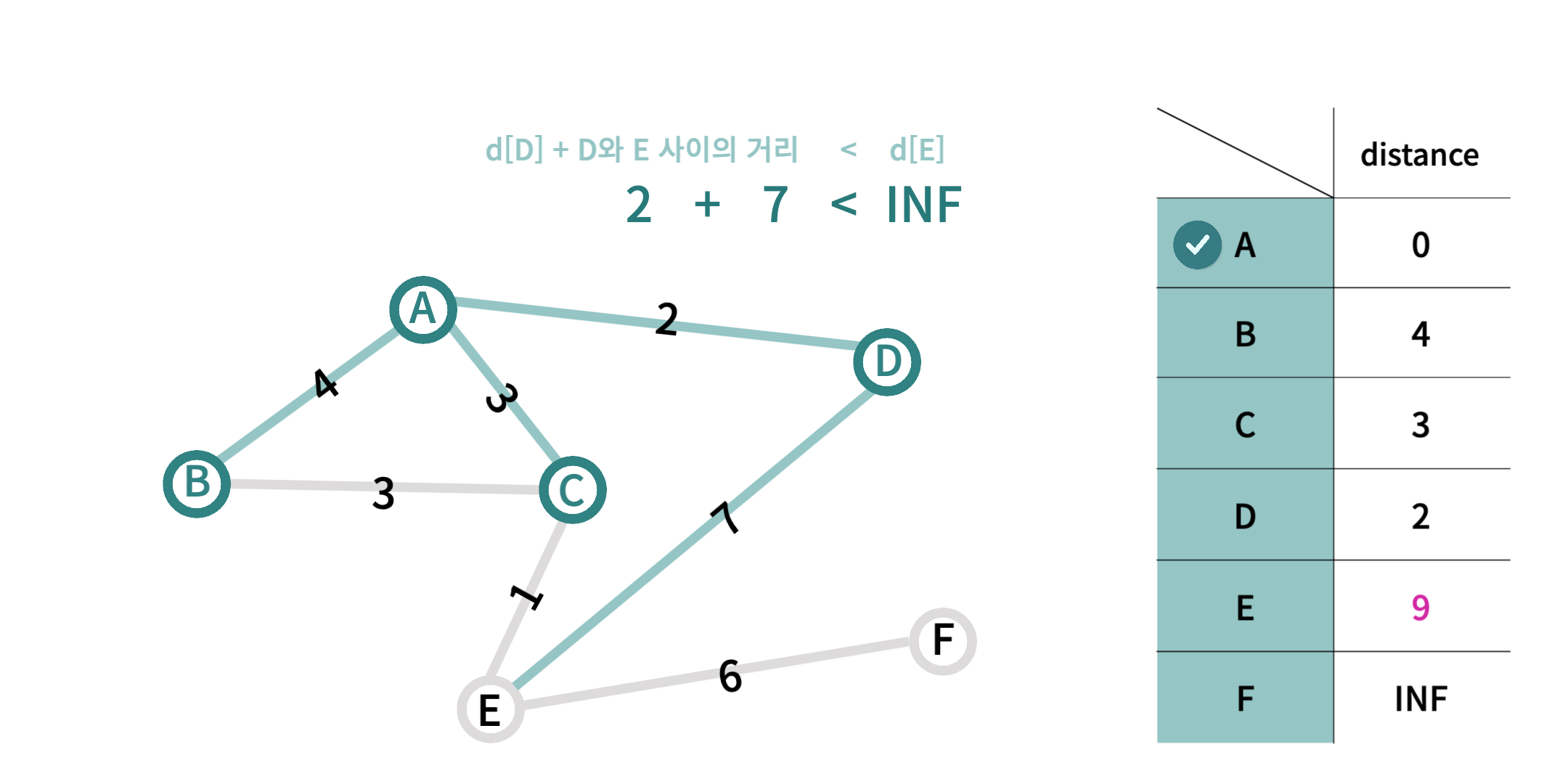
• 방문 완료가 아닌 노드 중에 가장 거리가 가까운 노드인 D 지점을 현재 노드로 지정한다.
• 현재 노드의 이웃 노드인 E 지점 까지의 거리는 d[D] + 두 지점 사이의 거리 의 값이 기존값 d[E] 보다 작으므로 새로운 값 9 로 갱신된다.
• D 지점 은 모든 이웃 노드를 방문하였으므로 더이상 사용하지 않는다. ( 방문 완료 )

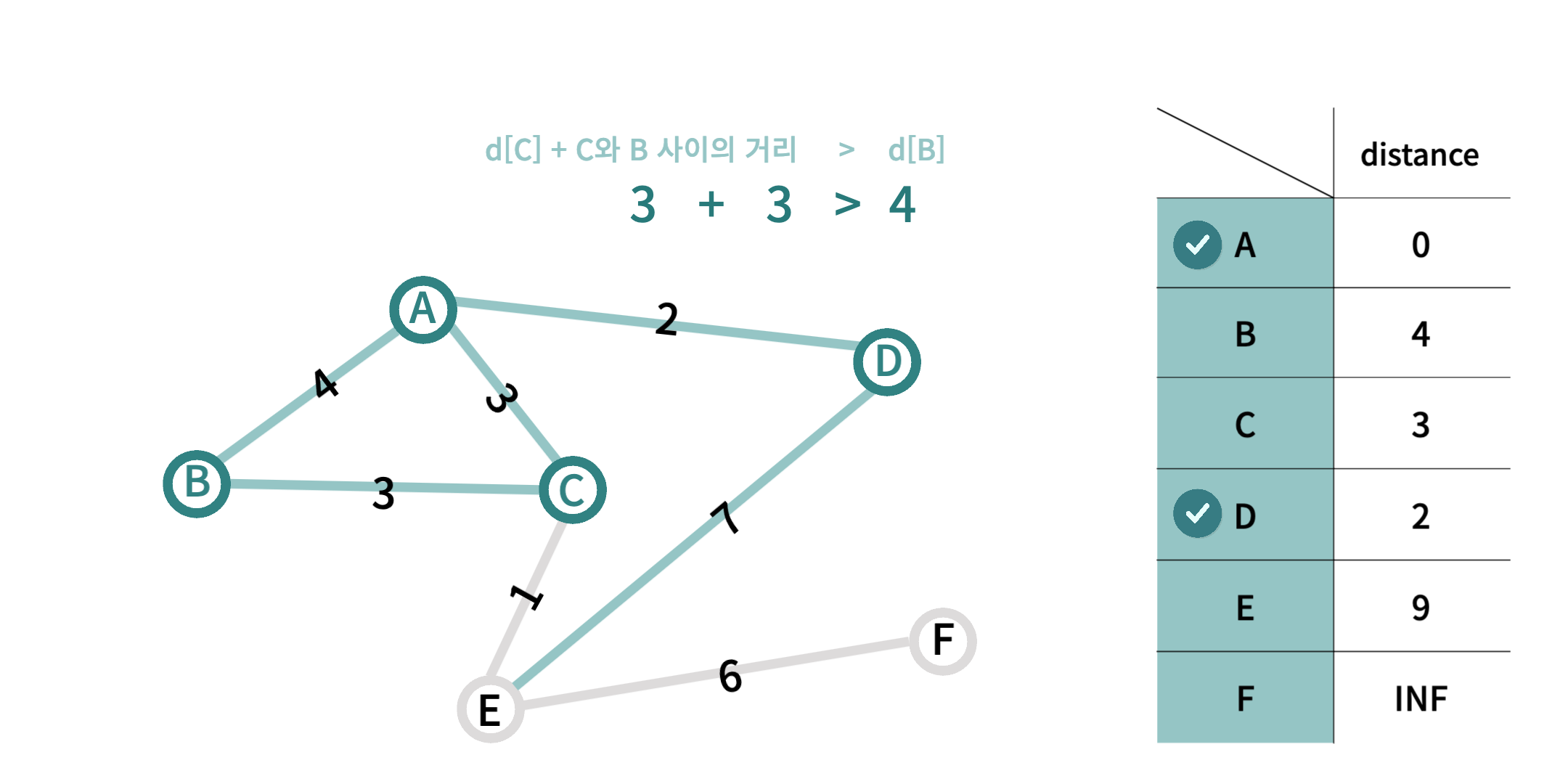
• 그 다음으로 출발점으로부터의 거리가 짧은 C 지점을 현재 노드로 지정한다.
• C 지점 의 이웃 노드는 A, B, E 지점이 있고, A 지점은 방문 완료 노드이므로 재방문 하지 않는다.
• B 지점 까지의 거리는 d[C] + 두 지점 사이의 거리 의 값이 기존값 d[B] 보다 크므로 새로운 값으로 갱신되지 않는다.

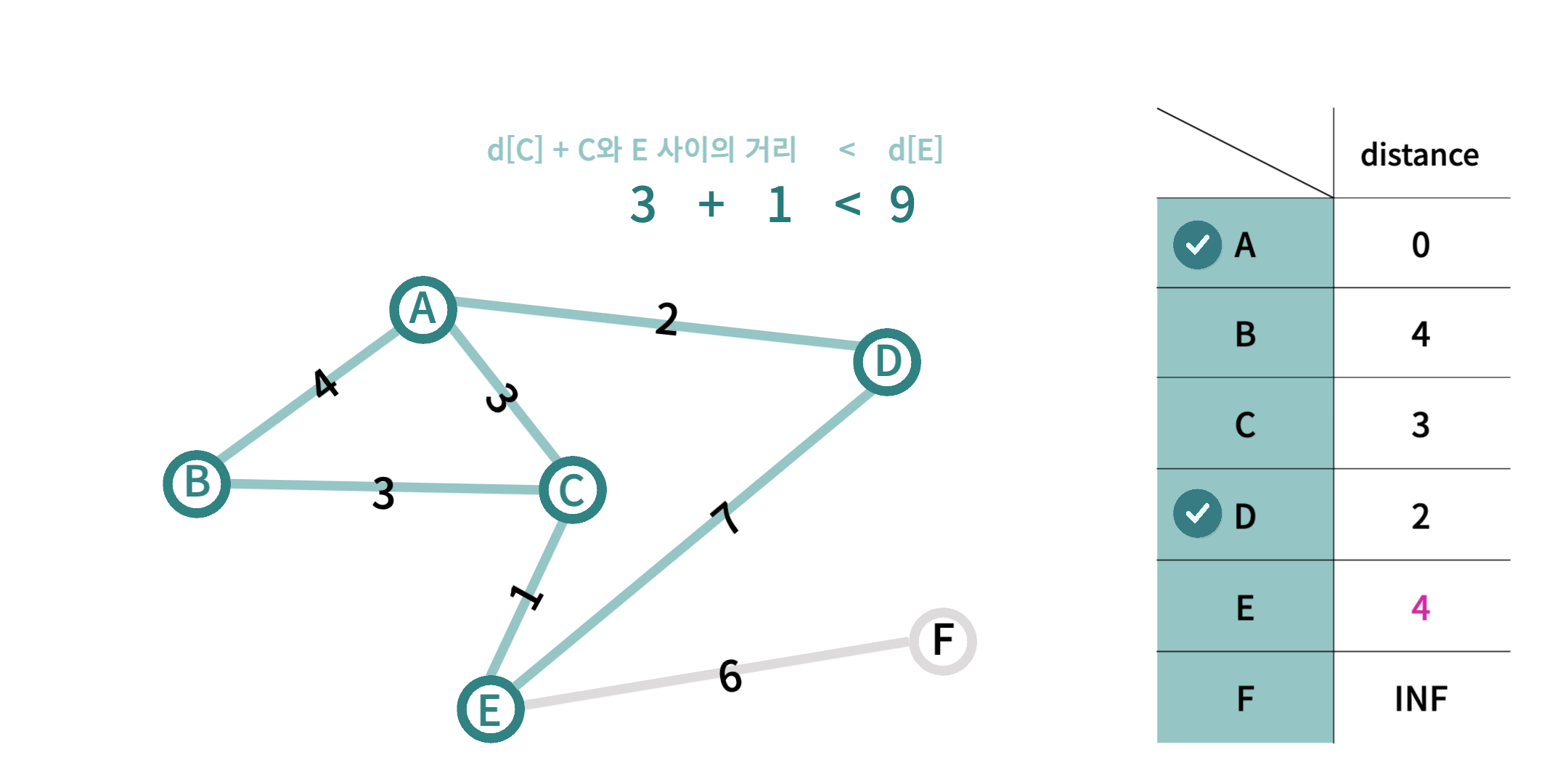
• E 지점 까지의 거리는 d[C] + 두 지점 사이의 거리 의 값이 기존값 d[E] 보다 작으므로 새로운 값 4 로 갱신된다.
• C 지점 은 모든 이웃 노드를 방문하였으므로 더이상 사용하지 않는다.
• B 지점 은 모든 이웃 노드가 방문 완료 이므로 해당 지점도 방문 완료 처리한다.

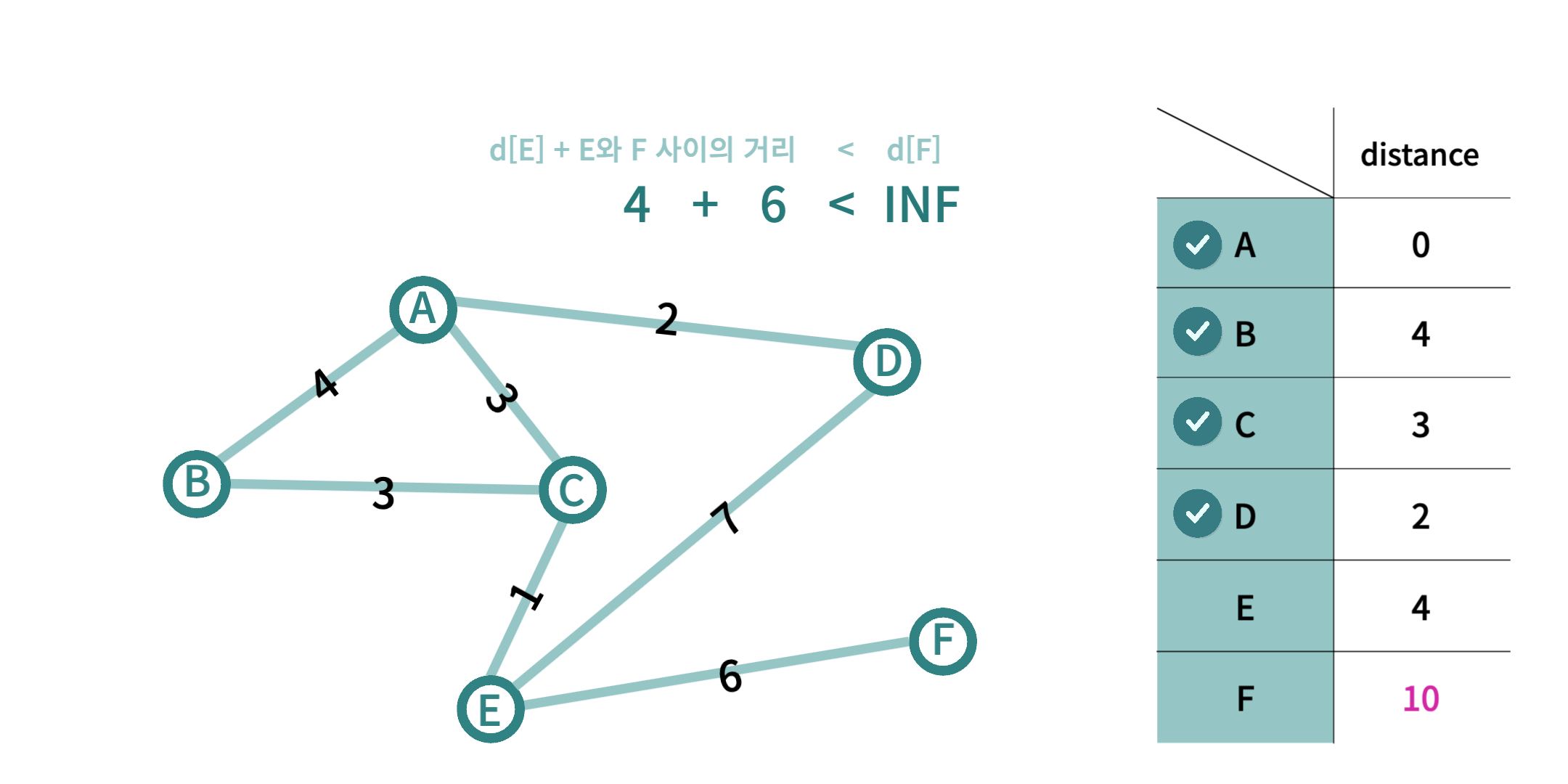
• 방문 완료가 아닌 노드 중에 가장 거리가 가까운 노드인 E 지점을 현재 노드로 지정한다.
• F 지점 까지의 거리는 d[E] + 두 지점 사이의 거리 의 값이 기존값 d[F] 보다 작으므로 새로운 값 10 로 갱신된다.
• E 지점 은 모든 이웃 노드를 방문하였으므로 더이상 사용하지 않는다.
• F 지점 또한 방문 완료 상태가 되므로 탐색을 종료한다.

---

5 - 우선순위 큐를 활용한 구현

데이크스트라 알고리즘을 이용하여 풀 수 있는 문제인 백준 5972 - 택배배송 을 구현한다.

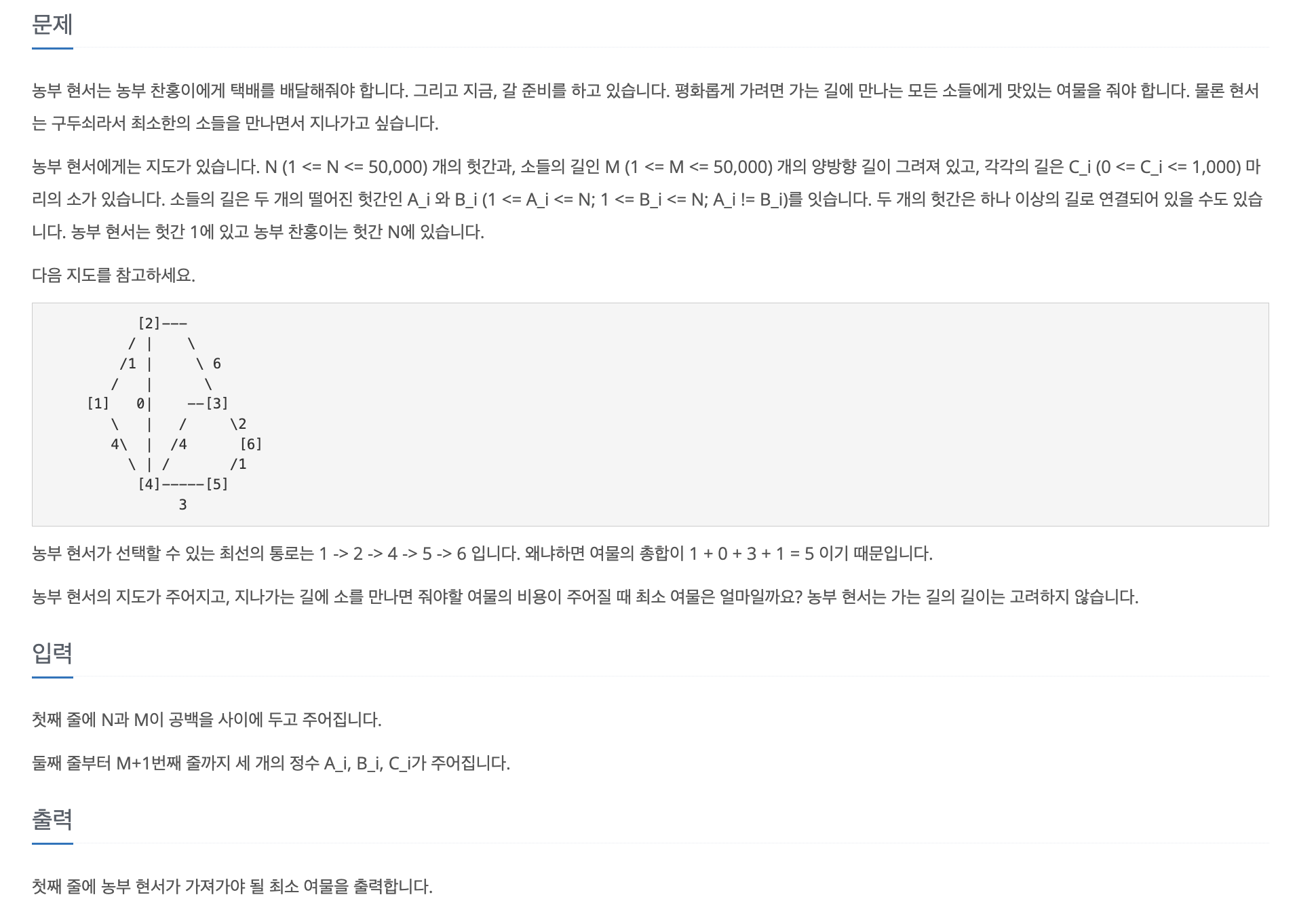
입력은 첫 줄에 정점의 개수 $N$, 간선의 개수 $M$ 이 주어지며 최단 경로의 출발지는 1번 지점, 도착지는 N번 지점이다.
둘째 줄부터는 지점번호 A, 지점번호 B, 두 지점 사이의 거리 C 가 주어진다.

  static ArrayList<Edge>[] list;
  static int[] cost;
  static final int INF = 50000*1000;
   
  private static class Edge implements Comparable<Edge> {
  	int end;
  	int val;

  	public Edge(int end, int val) {
  		this.end = end;
  		this.val = val;
  	}

  	@Override
  	public int compareTo(Edge e) {
  		return this.val - e.val;
  	}
 }

• ArrayList<Edge>[] list : 각 정점에 연결된 간선의 정보를 담을 수 있도록 간선 ArrayList의 배열을 선언한다. 배열의 크기는 N+1.
• int[] cost : 출발 지점으로부터 각 정점까지의 거리를 담는 배열. 배열의 크기는 N+1.
• int INF : cost 배열의 초기값. (최대 정점 수 * 간선의 최대 길이)
• class Edge : 간선을 클래스로 선언. end 는 간선의 끝점, val 은 간선의 길이.
• Comparable : 우선순위 큐에서 간선의 길이가 작은 간선이 앞에 놓이도록 compareTo 를 Override 한다.
  
  
  

StringTokenizer st;
Arrays.fill(cost, INF);

for(int i=0; i<M; i++) {
	st = new StringTokenizer(br.readLine());
	int s = Integer.parseInt(st.nextToken()); // 정점1
	int e = Integer.parseInt(st.nextToken()); // 정점2
	int v = Integer.parseInt(st.nextToken()); // 두 정점 사이의 거리

	list[s].add(new Edge(e, v));
	list[e].add(new Edge(s, v));
}

• cost 배열을 INF 로 초기화한다.
• list 배열 각 정점의 인덱스에 간선을 추가한다.
• 무방향 간선이므로 정점1, 정점2 모두에 간선을 추가한다.
  
  

private static void dijkstra(int start) {
	PriorityQueue<Edge> pq = new PriorityQueue<>();
    pq.add(new Edge(start, 0));
  	cost[start] = 0;

    while (!pq.isEmpty()) {
    	Edge cur = pq.poll();
    	for(Edge next : list[cur.end]) {
    		if(cost[next.end] > cost[cur.end] + next.val) {
    			cost[next.end] = cost[cur.end] + next.val;
    			pq.add(new Edge(next.end, cost[next.end]));
    		}
		}
	}
}

• 우선순위 큐에 시작점을 추가한다. 시작점의 cost = 0 이다.
• 큐가 비어있지 않다면 가장 앞(간선의 길이가 작은)의 요소를 poll() 한다.
• 현재 노드에 연결된 이웃 노드 중에서 현재 노드까지 거리 + 현재 노드에서 이웃 노드까지 거리 값이 이웃 노드에 저장된 값 보다 작다면 그 값을 갱신한다.
• 값을 갱신하는 경우 (이웃 노드, cost[이웃 노드]) 의 값을 갖는 새로운 간선을 우선순위 큐에 추가한다.
  
  

dijkstra(1);
System.out.println(cost[N]);

• 메인 함수에서 dijkstra(시작점) 를 호출한다.
• 다익스트라 함수가 종료된 후 cost 배열의 N번 인덱스에 저장된 값이 N 지점까지 가는 최단경로이다.
  
  
  

전체 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
    static int N, M;
    static ArrayList<Edge>[] list;
    static int[] cost;
    static final int INF = 50000*1000;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());

        cost = new int[N+1];
        Arrays.fill(cost, INF);
        list = new ArrayList[N+1];
        for(int i=0; i<=N; i++) list[i] = new ArrayList<>();

        for(int i=0; i<M; i++) {
            st = new StringTokenizer(br.readLine());
            int s = Integer.parseInt(st.nextToken());
            int e = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());

            list[s].add(new Edge(e, v));
            list[e].add(new Edge(s, v));
        }
        dijkstra(1);
        System.out.println(cost[N]);
    }
    private static void dijkstra(int start) {
        PriorityQueue<Edge> pq = new PriorityQueue<>();
        pq.add(new Edge(start, 0));
        cost[start] = 0;

        while (!pq.isEmpty()) {
            Edge cur = pq.poll();
            for(Edge next : list[cur.end]) {
                if(cost[next.end] > cost[cur.end] + next.val) {
                    cost[next.end] = cost[cur.end] + next.val;
                    pq.add(new Edge(next.end, cost[next.end]));
                }
            }
        }
    }
    private static class Edge implements Comparable<Edge> {
        int end;
        int val;

        public Edge(int end, int val) {
            this.end = end;
            this.val = val;
        }

        @Override
        public int compareTo(Edge e) {
            return this.val - e.val;
        }
    }
}