백준 12891 - DNA 비밀번호

문제

시간 제한 2초

평소에 문자열을 가지고 노는 것을 좋아하는 민호는 DNA 문자열을 알게 되었다. DNA 문자열은 모든 문자열에 등장하는 문자가 {‘A’, ‘C’, ‘G’, ‘T’} 인 문자열을 말한다. 예를 들어 “ACKA”는 DNA 문자열이 아니지만 “ACCA”는 DNA 문자열이다. 이런 신비한 문자열에 완전히 매료된 민호는 임의의 DNA 문자열을 만들고 만들어진 DNA 문자열의 부분문자열을 비밀번호로 사용하기로 마음먹었다.

하지만 민호는 이러한 방법에는 큰 문제가 있다는 것을 발견했다. 임의의 DNA 문자열의 부분문자열을 뽑았을 때 “AAAA”와 같이 보안에 취약한 비밀번호가 만들어 질 수 있기 때문이다. 그래서 민호는 부분문자열에서 등장하는 문자의 개수가 특정 개수 이상이여야 비밀번호로 사용할 수 있다는 규칙을 만들었다.

임의의 DNA문자열이 “AAACCTGCCAA” 이고 민호가 뽑을 부분문자열의 길이를 4라고 하자. 그리고 부분문자열에 ‘A’ 는 1개 이상, ‘C’는 1개 이상, ‘G’는 1개 이상, ‘T’는 0개 이상이 등장해야 비밀번호로 사용할 수 있다고 하자. 이때 “ACCT” 는 ‘G’ 가 1 개 이상 등장해야 한다는 조건을 만족하지 못해 비밀번호로 사용하지 못한다. 하지만 “GCCA” 은 모든 조건을 만족하기 때문에 비밀번호로 사용할 수 있다.

민호가 만든 임의의 DNA 문자열과 비밀번호로 사용할 부분분자열의 길이, 그리고 {‘A’, ‘C’, ‘G’, ‘T’} 가 각각 몇번 이상 등장해야 비밀번호로 사용할 수 있는지 순서대로 주어졌을 때 민호가 만들 수 있는 비밀번호의 종류의 수를 구하는 프로그램을 작성하자. 단 부분문자열이 등장하는 위치가 다르다면 부분문자열이 같다고 하더라도 다른 문자열로 취급한다.

입력

첫 번째 줄에 민호가 임의로 만든 DNA 문자열 길이 |S|와 비밀번호로 사용할 부분문자열의 길이 |P| 가 주어진다. (1 ≤ |P| ≤ |S| ≤ 1,000,000)

두번 째 줄에는 민호가 임의로 만든 DNA 문자열이 주어진다.

세번 째 줄에는 부분문자열에 포함되어야 할 {‘A’, ‘C’, ‘G’, ‘T’} 의 최소 개수가 공백을 구분으로 주어진다. 각각의 수는 |S| 보다 작거나 같은 음이 아닌 정수이며 총 합은 |S| 보다 작거나 같음이 보장된다.

출력

첫 번째 줄에 민호가 만들 수 있는 비밀번호의 종류의 수를 출력해라.

문제풀이

이 문제를 풀 때는 슬라이딩 윈도우 알고리즘을 사용하면 된다. 슬라이딩 윈도우 알고리즘은 2개의 포인터로 범위를 지정한 다음 범위를 유지한 채로 이동하여 푸는 방식이다.
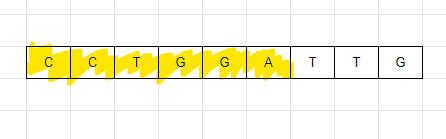{C, C, T, G, G, A} 배열을 확인해서 각 각의 최소 갯수를 구하면 {1, 2, 2, 1} 이다.
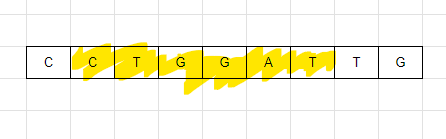그 후 크기를 유지한 상태로 이동 한 후 확인하다.

{C, T, G, G, A, T} 배열을 확인해서 각 각의 최소 갯수를 구하면 {1, 1, 2, 2} 이다.

이런 식으로 슬라이딩 윈도우를 코드에 적용시키면 된다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

class DNA비밀번호 {
    private static int[] check;         // A, C, G, T 최소 개수
    private static int[] my_check;      // 부분 문자열이 적합한지 체크
    private static int checkSecret;      // 비밀번호로 적합한지 체크

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int S = Integer.parseInt(st.nextToken()); // DNA 문자열 길이
        int P = Integer.parseInt(st.nextToken()); // 부분문자열 길이

        int result = 0;                          // 정답
        check = new int[4];
        my_check = new int[4];
        checkSecret = 0;

        char[] DNA = br.readLine().toCharArray(); // 입력받은 DNA

        st = new StringTokenizer(br.readLine());
        for(int i = 0; i < 4; i++){
            check[i] = Integer.parseInt(st.nextToken());
            if(check[i] == 0)
                checkSecret++;
        }

        for(int i = 0; i < P; i++){
            Add(DNA[i]);
        }

        if(checkSecret == 4)
            result++;

        for(int i = P; i < S; i++) {
            int j = i - P;
            Add(DNA[i]);
            Remove(DNA[j]);
            if(checkSecret == 4)
                result++;

        }
        System.out.println(result);

    }

    private static void Remove(char c) {
        switch (c) {
            case 'A':
                if (check[0] == my_check[0])
                    checkSecret--;
                my_check[0]--;
                break;
            case 'C':
                if (check[1] == my_check[1])
                    checkSecret--;
                my_check[1]--;
                break;
            case 'G':
                if (check[2] == my_check[2])
                    checkSecret--;
                my_check[2]--;
                break;
            case 'T':
                if (check[3] == my_check[3])
                    checkSecret--;
                my_check[3]--;
                break;
        }
    }

    private static void Add(char c) {
        switch (c) {
            case 'A':
                my_check[0]++;
                if (check[0] == my_check[0])
                    checkSecret++;
                break;
            case 'C':
                my_check[1]++;
                if (check[1] == my_check[1])
                    checkSecret++;
                break;
            case 'G':
                my_check[2]++;
                if (check[2] == my_check[2])
                    checkSecret++;
                break;
            case 'T':
                my_check[3]++;
                if (check[3] == my_check[3])
                    checkSecret++;
                break;
        }
    }

}	

회고

Do it! 알고리즘 코딩 테스트 책을 보지 않고 풀어보았을때는 코드를 구현하기 어려웠다. 특히 슬라이딩 윈도우 알고리즘과 함수를 적용하는 것을 보니 아직 알고리즘을 매우매우 많이 풀어봐야겠다는 것을 알게 되었다.