백준 1517 - 버블소트

문제

시간 제한 1초

N개의 수로 이루어진 수열 A[1], A[2], …, A[N]이 있다. 이 수열에 대해서 버블 소트를 수행할 때, Swap이 총 몇 번 발생하는지 알아내는 프로그램을 작성하시오.

버블 소트는 서로 인접해 있는 두 수를 바꿔가며 정렬하는 방법이다. 예를 들어 수열이 3 2 1 이었다고 하자. 이 경우에는 인접해 있는 3, 2가 바뀌어야 하므로 2 3 1 이 된다. 다음으로는 3, 1이 바뀌어야 하므로 2 1 3 이 된다. 다음에는 2, 1이 바뀌어야 하므로 1 2 3 이 된다. 그러면 더 이상 바꿔야 할 경우가 없으므로 정렬이 완료된다.

입력

첫째 줄에 N(1 ≤ N ≤ 500,000)이 주어진다. 다음 줄에는 N개의 정수로 A[1], A[2], …, A[N]이 주어진다. 각각의 A[i]는 0 ≤ |A[i]| ≤ 1,000,000,000의 범위에 들어있다.

출력

첫째 줄에 Swap 횟수를 출력한다

예제 입력 1

3
3 2 1

예제 출력 1

3

문제 풀이

처음 문제 이름 자체가 버블 소트여서 버블정렬을 이용한 문제이겠구나 생각했다.

하지만 N의 최댓값은 500,000 이어서 버블정렬의 시간복잡도인 $O(n^2)$ 으로는 시간초과가 난다.

따라서 시간복잡도가 $O(nlogn)$인 병합정렬을 이용하면 서로 swap 하는 과정이 있기 때문에 병합정렬을 이용한 문제임을 알게 되었다.

전 게시글에서 풀었던 병합 정렬 기능과 유사하게 풀면 문제는 해결이 가능하다.

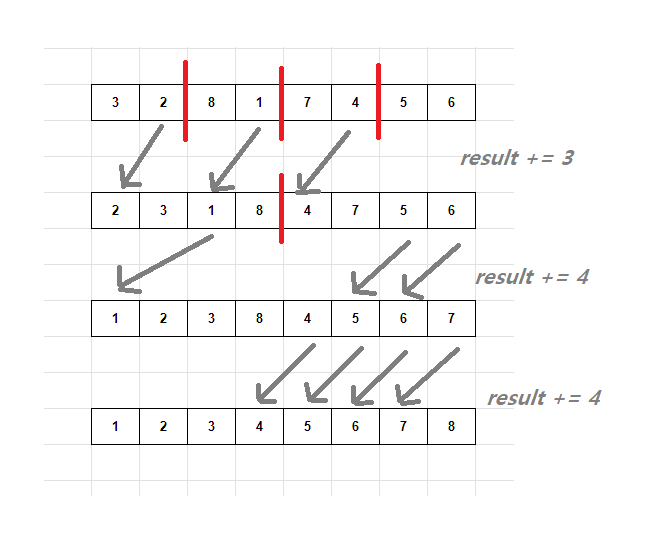
이 때 그룹끼리 정령을 할 때 원소가 이동한 거리 == swap 횟수 라는 결론에 도달한다.

유튜브를 참고해서 얻게 되었다.

참고 영상 : https://youtu.be/IEc2fRD5d0k

import java.io.*;
import java.util.*;

public class 버블소트 {

    private static int[] A, tmp;
    private static long result;   // int로 할 경우에 에러 발생!!

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());

        A = new int[N + 1];
        tmp = new int[N + 1];

        StringTokenizer st = new StringTokenizer(br.readLine());
        for(int i = 1; i <= N; i++) {
            A[i] = Integer.parseInt(st.nextToken());
        }

        merge_sort(1, N);

        System.out.println(result);
    }

    private static void merge_sort(int start, int end) {

        if(end - start < 1)
            return;

        int mid = start + (end - start) / 2;
        merge_sort(start, mid);
        merge_sort(mid + 1, end);

        for(int i = start; i <= end; i++) {
            tmp[i] = A[i];
        }
        int k = start;
        int part1 = start;
        int part2 = mid + 1;
        while(part1 <= mid && part2 <= end) {
            if(tmp[part1] > tmp[part2]) {
                A[k] = tmp[part2];
                result += part2 - k;	// 중요!! 
                k++;
                part2++;
            }else {
                A[k] = tmp[part1];
                k++;
                part1++;
            }
        }

        while(part1 <= mid) {
            A[k] = tmp[part1];
            k++;
            part1++;
        }

        while(part2 <= end) {
            A[k] = tmp[part2];
            k++;
            part2++;
        }
    }
}

회고

swap의 총 횟수를 구하는 방법을 결국 찾지 못해서 유튜브를 참고하게 되었다.
또한 result를 int 형식으로 제출했을 때는 에러가 나서 내가 뭔가를 잘못 풀었나 생각했지만 책에는 long 형식으로 되어 있어서 변환을 해주었더니 오류없이 잘 해결 되었다.
가급적이면 long을 습관화들이는게 좋을거 같다.

어떻게 저런 문제풀이가 나오는지 너무나 궁금할 따름이다...