백준 1715 - 카드 정렬하기

YongHyun·2023년 5월 9일

백준, 프로그래머스 - 코딩테스트

목록 보기

33/43

문제

정렬된 두 묶음의 숫자 카드가 있다고 하자. 각 묶음의 카드의 수를 A, B라 하면 보통 두 묶음을 합쳐서 하나로 만드는 데에는 A+B 번의 비교를 해야 한다. 이를테면, 20장의 숫자 카드 묶음과 30장의 숫자 카드 묶음을 합치려면 50번의 비교가 필요하다.

매우 많은 숫자 카드 묶음이 책상 위에 놓여 있다. 이들을 두 묶음씩 골라 서로 합쳐나간다면, 고르는 순서에 따라서 비교 횟수가 매우 달라진다. 예를 들어 10장, 20장, 40장의 묶음이 있다면 10장과 20장을 합친 뒤, 합친 30장 묶음과 40장을 합친다면 (10 + 20) + (30 + 40) = 100번의 비교가 필요하다. 그러나 10장과 40장을 합친 뒤, 합친 50장 묶음과 20장을 합친다면 (10 + 40) + (50 + 20) = 120 번의 비교가 필요하므로 덜 효율적인 방법이다.

N개의 숫자 카드 묶음의 각각의 크기가 주어질 때, 최소한 몇 번의 비교가 필요한지를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N이 주어진다. (1 ≤ N ≤ 100,000) 이어서 N개의 줄에 걸쳐 숫자 카드 묶음의 각각의 크기가 주어진다. 숫자 카드 묶음의 크기는 1,000보다 작거나 같은 양의 정수이다.

출력

첫째 줄에 최소 비교 횟수를 출력한다.

예제 입력 1

3
10
20
40

예제 출력 1

100

문제 풀이

N 개의 숫자 카드 묶음의 각각의 크기가 주어질 때, 최소한 몇 번의 비교가 필요한지를 구하는 프로그램을 작성하시오. 라는 문구가 중요한 것 같다.

예를 들어 10, 20, 40 의 숫자 카드 묶음이 주어질 때 최소의 수를 구해야 하기 때문에 작은 카드 묶음 부터 합쳐줘야 한다.
즉, 10, 20 부터 합쳐줘야 최소의 수를 구할 수 있다.

이럴 때 우선순위 큐를 사용하면 어떨까? 합쳐진 수는 다시 다음 카드 묶음과 더해줘야 한다는 점과 항상 작은 카드 묶음 두 개를 찾아야 하기 때문에 자동으로 정렬시켜주는 우선순위 큐가 적절한 선택인것 같다.

그러면 우선순위 큐를 이용하영 단계별로 문제를 풀어보겠다.

PriorityQueue에 넣어준 10, 20, 40 은 우선순위에 따라 다음과 같은 상태로 정렬되어 있다. 이 때 poll() 을 두 번 실행 시켜서 작은 카드 묶음의 개수 10, 20 을 꺼내고 합을 구한다.

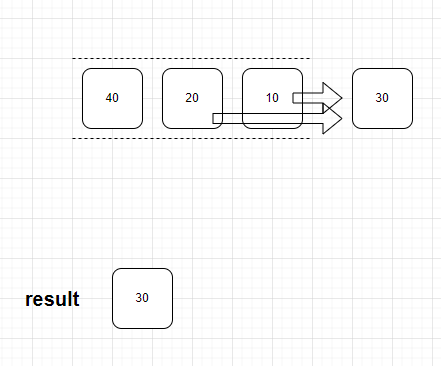
더한 합은 다시 PriorityQueue에 에 넣어주고 다음과 같이 우선순위에 따라 다시 정렬되고 poll() 을 두 번 실행 시켜 30, 40 을 꺼내고 합을 구한다.

PriorityQueue에 size() 가 1일 경우에는 반복문을 종료 시키고 누적 합 result 를 출력시키면 된다.

이를 코드에 적용시키면 다음과 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.PriorityQueue;
import java.util.Queue;

public class 카드정렬하기 {

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());

        Queue<Integer> queue = new PriorityQueue<>();

        int result = 0;
        for(int i = 0; i < N; i++) {
            int deck = Integer.parseInt(br.readLine());
            queue.offer(deck);
        }

        while(queue.size() != 1) {
            int first = queue.poll();
            int second = queue.poll();
            result += first + second;
            queue.offer(first + second);
        }
        System.out.println(result);

    }

}