문제
수빈이가 세상에서 가장 좋아하는 것은 소수이고, 취미는 소수를 가지고 노는 것이다. 요즘 수빈이가 가장 관심있어 하는 소수는 7331이다.
7331은 소수인데, 신기하게도 733도 소수이고, 73도 소수이고, 7도 소수이다. 즉, 왼쪽부터 1자리, 2자리, 3자리, 4자리 수 모두 소수이다! 수빈이는 이런 숫자를 신기한 소수라고 이름 붙였다.
수빈이는 N자리의 숫자 중에서 어떤 수들이 신기한 소수인지 궁금해졌다. N이 주어졌을 때, 수빈이를 위해 N자리 신기한 소수를 모두 찾아보자.
입력
첫째 줄에 N(1 ≤ N ≤ 8)이 주어진다.
출력
N자리 수 중에서 신기한 소수를 오름차순으로 정렬해서 한 줄에 하나씩 출력한다.
예제 입력 1
4
예제 출력 1
2333
2339
2393
2399
2939
3119
3137
3733
3739
3793
3797
5939
7193
7331
7333
7393
문제 풀이
N의 최댓값은 8로 매우 작기 때문에 시간복잡도는 그리 많이 고려하지 않아도 된다는 뜻이라고 한다.
그렇다면 이 문제는 DFS로 풀어도 괜찮다고 결론을 내릴 수 있다는데 아직 많은 문제를 접하지 못해서 그런지 유튜브나 책을 참고하지 않았을 때는 바로 도출하기 어려웟다.
핵심은 N의 최댓값이 작기 때문에 완전탐색기법인 DFS를 사용하면 일단 편하다는 것만 알아두겠다.
그럼 바로 문제로 들어가보겠다.
먼저 N이 4라고 가정하면 천의 자리에 올 수 있는 수는 어떤것이 있을까?
소수는 1과 자기 자신만을 약수로 가지는 수이기 때문에 들어갈 수 있는 수는 2, 3, 5, 7 이다.
그런다음 백의 자리에 올 수 있는 수는 어떤것이 있을까?
여기서 2, 3, 5, 7 로 분기가 나뉘어져서 재귀형태로 수행을 시킨다.
2를 기준으로 잡으면 20 ~ 29 사이의 소수를 찾으면 23, 26, 29 라는 수가 있다는 것을 알게된다.
그 다음 기준점은 23에 3을 기준으로 찾으면 233, 239 이다.
마지막 기준점은 233에 3을 통해서 소수를 찾으면 2333, 2339 이다.
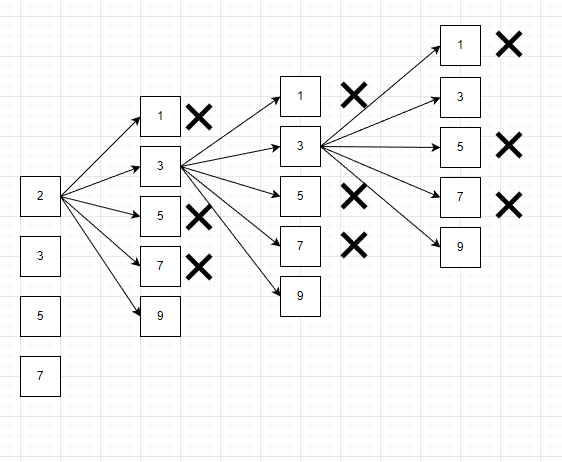
이때 알 수 있는 점은 처음 천의 자리는 2, 3, 5, 7 로 소수만 올 수 있지만 백의 자리 십의 자리 일의 자리는 홀수 또는 소수가 들어온다는 것이다.
그림으로 표현하면 다음과 같다.
그리고 소수를 판별하는 코드를 작성하는데 기억이 나지 않아서 검색을 해본 결과 에라토스테네스의 체라는 소수를 찾는 방법이 있어서 참고하였다.
에라토스테네스의 체
참고 자료 : https://velog.io/@max9106/Algorithm-%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98-%EC%B2%B4
이 문제에서는 어떠한 수의 소수를 판별할 때 그 수의 제곱근 까지만 약수의 여부를 검증하면 되는 코드로 작성하였다.
왜 제곱근 까지만 확인하면 되는 것인가?
https://nahwasa.com/entry/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98-%EC%B2%B4-%ED%98%B9%EC%9D%80-%EC%86%8C%EC%88%98%ED%8C%90%EC%A0%95-%EC%8B%9C-%EC%A0%9C%EA%B3%B1%EA%B7%BC-%EA%B9%8C%EC%A7%80%EB%A7%8C-%ED%99%95%EC%9D%B8%ED%95%98%EB%A9%B4-%EB%90%98%EB%8A%94-%EC%9D%B4%EC%9C%A0
이를 코드에 한번 적용해보겠다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class 신기한소수 {
private static int N;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
DFS(2, 1);
DFS(3, 1);
DFS(5, 1);
DFS(7, 1);
}
private static void DFS(int num, int jarisu) {
if(jarisu == N) {
if(findPrimeNumber(num)){
System.out.println(num);
}
return;
}
for(int i = 1; i < 10; i+=2) {
if (findPrimeNumber(num * 10 + i)) {
DFS(num * 10 + i, jarisu + 1);
}
}
}
private static boolean findPrimeNumber(int num) {
for(int i = 2; i <= num / 2; i++) {
if(num % i == 0) return false;
}
return true;
}
}
회고
소수를 판별하는 것을 까먹어서 에라토스테네스의 체 공식을 다시 공부하였다. 소수를 구하는 문제는 자주 나오기 때문에 확실히 공부해야 한다. 역시 공부하는 내용을 정리하는 습관을 많이 가져야겠다고 생각하게 되었다.