백준 2343 - 기타 레슨

문제

시간 제한 2초

강토는 자신의 기타 강의 동영상을 블루레이로 만들어 판매하려고 한다. 블루레이에는 총 N개의 강의가 들어가는데, 블루레이를 녹화할 때, 강의의 순서가 바뀌면 안 된다. 순서가 뒤바뀌는 경우에는 강의의 흐름이 끊겨, 학생들이 대혼란에 빠질 수 있기 때문이다. 즉, i번 강의와 j번 강의를 같은 블루레이에 녹화하려면 i와 j 사이의 모든 강의도 같은 블루레이에 녹화해야 한다.

강토는 이 블루레이가 얼마나 팔릴지 아직 알 수 없기 때문에, 블루레이의 개수를 가급적 줄이려고 한다. 오랜 고민 끝에 강토는 M개의 블루레이에 모든 기타 강의 동영상을 녹화하기로 했다. 이때, 블루레이의 크기(녹화 가능한 길이)를 최소로 하려고 한다. 단, M개의 블루레이는 모두 같은 크기이어야 한다.

강토의 각 강의의 길이가 분 단위(자연수)로 주어진다. 이때, 가능한 블루레이의 크기 중 최소를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 강의의 수 N (1 ≤ N ≤ 100,000)과 M (1 ≤ M ≤ N)이 주어진다. 다음 줄에는 강토의 기타 강의의 길이가 강의 순서대로 분 단위로(자연수)로 주어진다. 각 강의의 길이는 10,000분을 넘지 않는다.

출력

첫째 줄에 가능한 블루레이 크기중 최소를 출력한다.

예제 입력 1

9 3
1 2 3 4 5 6 7 8 9

예제 출력 1

17

문제 풀이

처음 문제를 봤을 때는 이해하기가 힘들었다. 그래서 몇번이나 읽어보면서 왜 이런 출력이 나오게 되었는지 이해하는데 시간을 많이 소비하였다.

여튼 문제를 요약하자면 기타 강의 동영상을 블루레이로 만들어 판매하기 위해서 가능한 블루레이의 크기(녹화 가능한 길이) 중 최소를 출력하는 것이다.
이때 블루레이를 녹화하려면 i와 j 사이의 모든 강의를 블루레이에 녹화해야 하고 M개의 블루레이는 모두 같은 크기여야 한다.

이를 예제 입력 1 에서 입력 받은 데이터로 표현하자면
강의 수 N 은 9, 블루레이의 수 M 은 3 이니 총 N 개의 데이터를 A라는 배열에 넣어주고 이 A라는 배열을 M개로 분할 시켜주는 것이다.

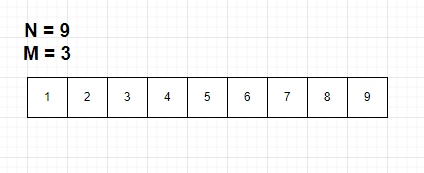
일단 임의로 배열을 {1, 2, 3, 4, 5} {6, 7} {8, 9} 로 나눴다고 가정하자

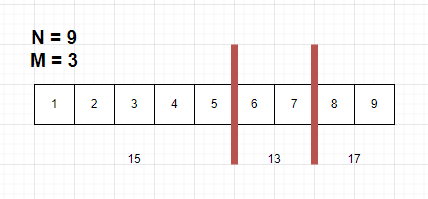
그러면 분할 시킨 배열에 있는 원소들을 더한 값은 각 각 15, 13, 17 이다. 이는 블루레이의 크기(녹화 가능한 길이)를 뜻하기도 한다.

그렇다면 17을 최소로 하면 15, 13 도 17보다는 작기 때문에 블루레이의 크기의 최소로 적합하니 정답은 17이다.

사실 여기서는 바로 정답을 출력하였지만 이런 결과를 도출하기 위해서는 블루레이의 크기를 이진 탐색 알고리즘을 사용하여서 도출해야 한다.

왜 이진 탐색 알고리즘이냐 하면 블루레이의 크기가 모두 같고 녹화 순서가 바뀌지 않아야 함이라는 문제 조건 때문이다.

이진 탐색 알고리즘은 중앙값을 이용하여 문제를 풀기 때문에 이 중앙값을 먼저 구하는 것이 포인트인데
시작 인덱스는 최대 길이의 레슨이고 종료 인덱스는 모든 레슨 길이의 합이다.
왜냐하면 예제 입력 1을 기준으로 본다면 1 ~ 9 사이의 최대 길이의 레슨을 1로 잡으면 나머지 2 ~ 9 는 레슨으로 포함될 수가 없다.
마찬가지로 2도 3 ~ 9 레슨은 포함할 수 없기 때문에 최대 길이는 9 로 정해야 한다.
그리고 종료 인덱스도 1 ~ 9 까지의 모든 합인 45 로 잡아야 한다.

그럼 이제 9 ~ 45 사이에서 이진탐색 과정을 거치면 된다.

• 이진탐색은 시작 인덱스 > 종료 인덱스일 때까지 수행한다.
• 중앙값 크기로 모든 레슨을 저장할 수 있다면 종료 인덱스 = 중앙값 - 1
• 중앙값 크기로 모든 레슨을 저장할 수 없으면 시작 인덱스 = 중앙값 + 1
  

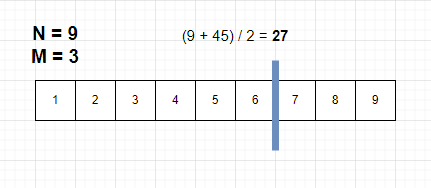
  중앙값 27로 블루레이의 크기는 27로 적합하지만 블루레이의 수는 2개로 조건과 맞지 않다.
  이럴 때는 종료 인덱스를 27 - 1 = 26으로 수정한 뒤 다시 탐색을 수행한다.

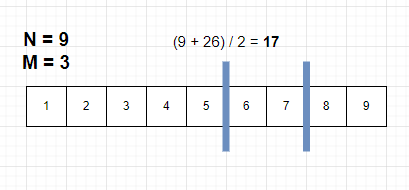
중앙값은 (9 + 26) / 2 = 17 이다 다시 종료 인덱스를 17 - 1 = 16으로 수정한 뒤 다시 탐색을 수행한다.

블루레이의 갯수가 맞지 않기 때문에 시작 인덱스를 12 + 1 = 13 으로 수정한 뒤 다시 탐색을 수행한다.

블루레이의 갯수가 맞지 않기 때문에 시작 인덱스를 14 + 1 = 15 으로 수정한 뒤 다시 탐색을 수행한다.

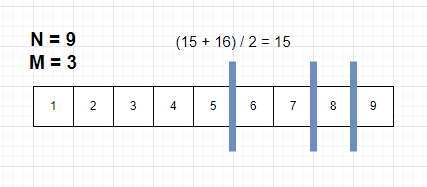
블루레이의 갯수가 맞지 않기 때문에 시작 인덱스를 15 + 1 = 16 으로 수정한 뒤 다시 탐색을 수행한다.

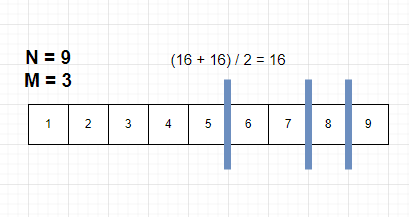
블루레이의 갯수가 맞지 않기 때문에 시작 인덱스를 16 + 1 = 17 으로 수정한다 이때
시작 인덱스 > 종료 인덱스 조건이 만족하기 때문에 시작 인덱스 17이 블루레이 크기의 최솟값이라는 결과가 도출된다.

이를 코드에 적용해보면 다음과 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class 기타레슨 {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int[] A = new int[N];
        st = new StringTokenizer(br.readLine());
        int start = 1;
        int end = 0;
        for(int i = 0; i < N; i++) {
            A[i] = Integer.parseInt(st.nextToken());
            if(start < A[i]){
                start = A[i];
            }
            end += A[i];
        }
        while(start <= end) {
            int mid = (start + end) / 2;
            int sum = 0;
            int count = 0;
            for(int i = 0; i < N; i++) {
                if(sum + A[i] > mid) {
                    count++;
                    sum = 0;
                }
                sum = sum + A[i];
            }
            if(sum != 0)
                count++;
            if(count > M)
                start = mid + 1;
            else
                end = mid - 1;
        }
        System.out.println(start);
    }
}

회고

사실 이진 탐색을 응용?? 하는 문제라고 생각하는데 이진 탐색 자체는 이해하는데 어려움은 없었지만 문제를 보고 이건 이진탐색으로 풀어야 한다는 생각은 아직 없는것 같다. 특히 이번 문제는 블루레이의 크기를 이용해서 이진탐색을 한다는 것 자체도 아직까지는 좀 아리송하다. 계속 문제를 훑어보면서 어떻게 이런 풀이 방법이 나오게 되었는지 꾸준히 공부해야 할 것 같다.