
바탕화면 정리
문제 풀이
문제의 지문만 읽는데도 시간이 좀 걸리긴 하지만 막상 계속 읽다보면 이해하기는 어렵지 않은 문제이다.
드래그 시작점 (lux, luy) 와 끝점(rdx, rdy) 를 배열 형태로 출력하면 되는데 이는 입출력 예 를 살펴보면 힌트를 얻을 수 있다.
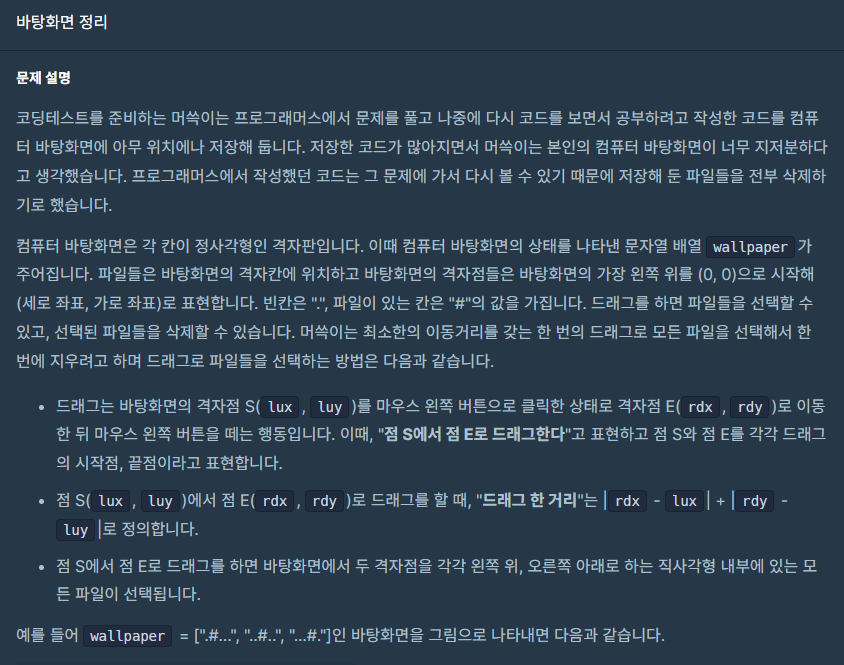
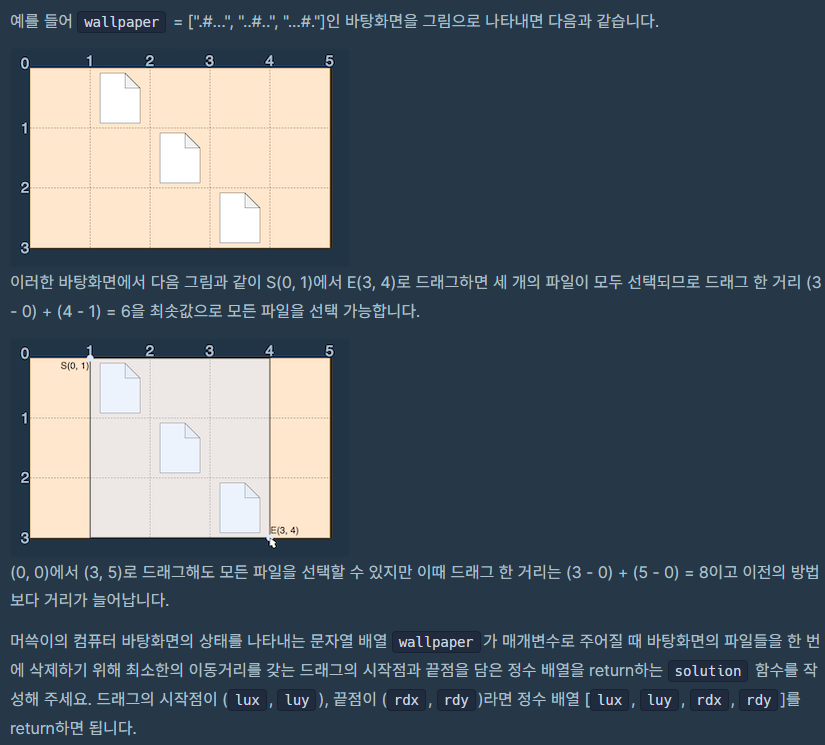
먼저 wallpaper 가 [".#...", "..#..", "...#."] 형태로 받았다고 가정해보자
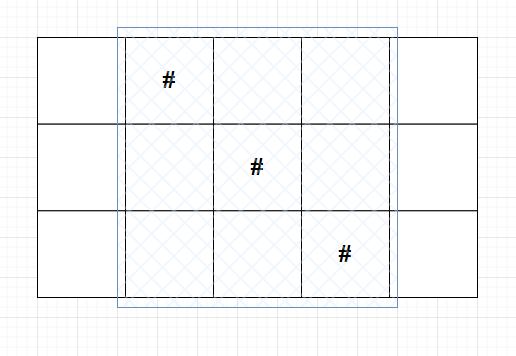
# 이 표시되어 있는 위치를 확인해보면 각 각 [0, 1], [1, 2], [2, 3] 에 존재한다.
최소한의 드래그를 해야 한다면 S [0, 1] 부터 E [2, 3] 까지 지정하면 된다.
이 때 잘 살펴보면 lux 는 int[x][y] 에서 x 중 가장 작은 수라는 것을 알 수 있다.
(0, 1, 2 중에서 가장 작은 값은 0 이다.)
다음은 luy 를 살펴보자 1, 2, 3 중 가장 작은 값은 1이다.
rdx 는 x 중 가장 큰 값을 rdy 도 마찬가지로 y 중 가장 큰 수라는 것을 알 수 있다.
한번 더 살펴보겠다. wallpaper 가 [".##...##.", "#..#.#..#", "#...#...#", ".#.....#.", "..#...#..", "...#.#...", "....#...."] 형태로 받았다고 가정해보자
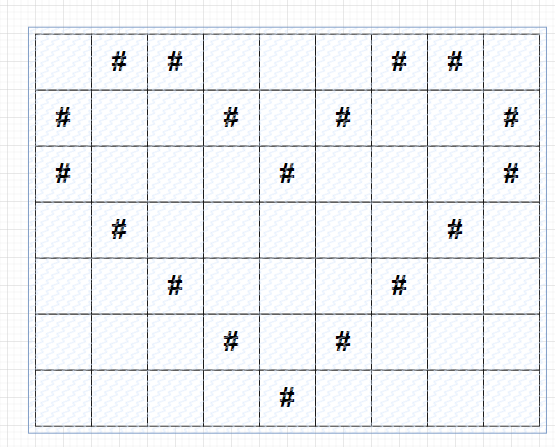
순서대로 # 의 위치를 출력해보면 다음과 같다.
0. [0, 1], [0, 2], [0, 6], [0, 7]
1. [1, 0], [1, 3], [1, 5], [0, 8]
2. [2, 1], [2, 4], [2, 8]
3. [3, 1], [3, 7]
4. [4, 2], [4, 6]
5. [5, 3], [5, 5]
6. [6, 4]
int[x][y]
그렇다면 lux 는 [x] 중 최솟값 luy 는 [y] 중 최솟값 이면 각 각 lux = 0, luy = 0 이다.
rdx 는 [x] 중 최댓값 luy 는 [y] 중 최댓값 으로 각 각 rdx = 6, rdy = 8 이다.
그리고 rdx 와 rdy 에는 각 각 1을 더해준다. 이유는 점을 기준으로 드래그 하기 때문이다.
따라서 결과값은 int[]{0, 0, 7, 9} 이다.
이를 코드에 적용하면 다음과 같다.
class Solution {
public int[] solution(String[] wallpaper) {
int lux = Integer.MAX_VALUE;
int luy = Integer.MAX_VALUE;
int rdx = 0;
int rdy = 0;
for(int i = 0; i < wallpaper.length; i++) {
String wp = wallpaper[i];
for(int j = 0; j < wallpaper[i].length(); j++) {
if (wp.charAt(j) == '#') {
lux = Math.min(lux, i);
luy = Math.min(luy, j);
rdx = Math.max(rdx, i + 1);
rdy = Math.max(rdy, j + 1);
}
}
}
return new int[]{lux, luy, rdx, rdy};
}
}
회고
규칙성을 찾지 못해서 이 문제도 푸는데 참 많은 시간을 사용하였다. 2차원 배열을 직접 만들어서 풀기도 하다가 도저히 안되서 구글링을 통해서 문제를 풀게 되었다.
이렇게 코드를 보니 간결하고 참 좋은 것 같으면서 혼자서 풀지 못한 것이 마음에 좀 걸린다.
