문제

문제를 살펴보자
득수 밥먹이기 : https://www.acmicpc.net/problem/24464

문제

프로젝트 하느라 바쁜 득수는 밥 먹을 시간이 부족하다. 그래서 주로 찾는 식당 네 개 중 하나에서 하루에 한 번 밥을 먹는다. 귀찮으면 굶을 때도 있다.

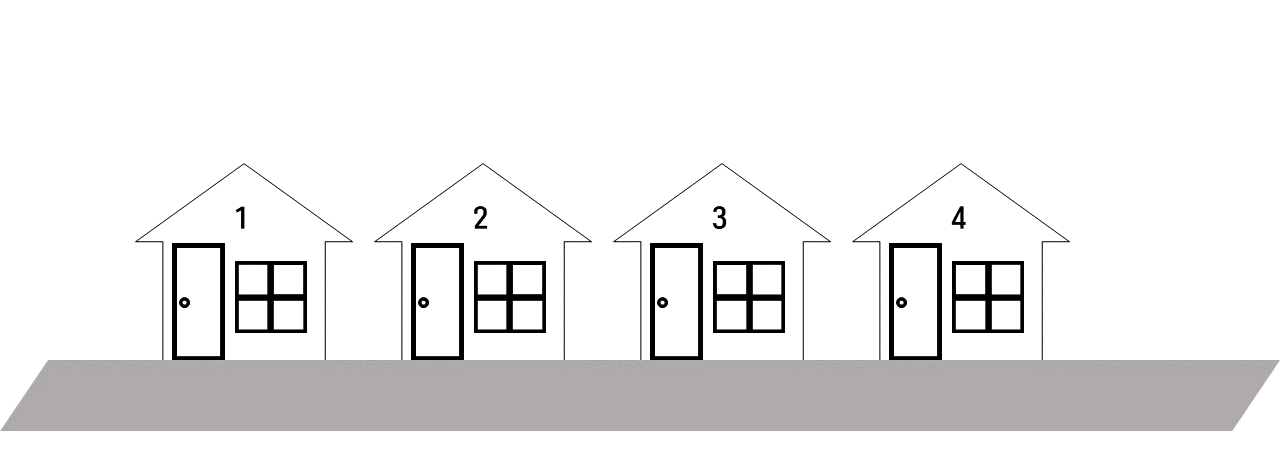
늘 새로운 느낌을 받고 싶었던 득수는 다음과 같은 규칙으로 다음날 갈 식당을 정한다.

첫날에는 굶거나, 임의로 원하는 식당 하나를 골라서 간다.
어제 굶지 않았다면, 오늘은 식당을 가지 않아도 된다.
어제 식당을 가지 않았다면, 오늘은 식당을 가서 밥을 먹어야 한다.
오늘 간 식당은 다음날 가지 않는다.
오늘 간 식당과 이웃한 식당은 다음날 가지 않는다.
만약 2번 식당을 오늘 갔다면, 다음날 $1$, $2$, $3$번 식당은 가지 않는다. 따라서 새로운 느낌을 받으려면 $4$번 식당을 가거나 굶어야 한다.

득수가 $N$일 치 식단표를 만들려고 한다. 위 규칙을 따라 식단표를 만들 때 가능한 경우의 수를 구하는 프로그램을 작성하시오.

입력

첫 번째 줄에는 득수가 만들어야 하는 점심 식단의 총 날짜 $N$이 입력으로 들어온다. $(1 \le N \le 200\,000)$

출력

 $N$일 치 식단표를 만들 때 가능한 경우의 수를 $1\,000\,000\,007(=10^9+7)$로 나눈 나머지를 출력한다.

예제입력1

1

예제출력1

5

예제입력2

2

예제출력2

14

풀이방법

해당 문제는 전형적인 DP이다.
n일차에 1번 식당을 먹을 수 있는 경우는 n-1일차에 2번식당 3번식당 혹은 안먹은 경우
2번 식당을 먹을 수 있는 경우는 n-1일차에 3번식당 혹은 안먹은 경우
3번 식당은 1번식당 혹은 안먹은 경우
4번 시당은 1번식당, 2번식당, 안먹은 경우이다.
안먹은 경우는 전일차에 식당에 들려서 먹기만 하면 된다.
1번식당을 0번째 2번식당을 1번째 3번식당을 2번째 4번식당을 3번째 안먹은 경우를 4번째 배열로 두고 이를 점화식으로 나타내면
dp[n][0]=dp[n-1][2]+dp[n-1][3]+dp[n-1][4]
dp[n][1]=dp[n-1][3]+dp[n-1][4]
dp[n][2]=dp[n-1][1]+dp[n-1][4]
dp[n][3]=dp[n-1][0]+dp[n-1][1]+dp[n-1][4]
dp[n][4]=dp[n-1][0]+dp[n-1][1]+dp[n-1][2]+dp[n-1][3]
이다
이때 주의할 점은 N이 200000이다. 이를 다 변수로 저장하면 메모리 초과가 나오게 된다.
어짜피 우리에게 필요한것은 바로 전일만 필요하기에 전일의 값만 저장해서 활용한다.

코드

n=int(input())
dp=[1,1,1,1,1]
for i in range(1,n):
    t=[0,0,0,0,0]#오늘 값을 계산할 예정 현재 dp는 전일의 값을 저장 중
    t[0]=(dp[2]+dp[3]+dp[4])%1000000007
    t[1]=(dp[3]+dp[4])%1000000007
    t[2]=(dp[0]+dp[4])%1000000007
    t[3]=(dp[0]+dp[1]+dp[4])%1000000007
    t[4]=(sum(dp[:4]))%1000000007
    dp=t[:]#오늘의 값을 다시 dp에 저장
print(sum(dp)%1000000007)#나머지를 까먹지 말자

후기

이 문제는 전형적인 DP문제라 많이 쉽게 풀었다. DP문제는 점화식을 발견하면 참 쉬운데 그게 안떠오르면 참 어려운거 같다. 많은 유형을 풀어서 대부분이 전형적으로 느껴지게 만들어야 하나...
그리고 나머지 해야하는데 항상 자주 까먹는거 같다. 문제 풀때 문제를 꼼꼼히 보자.