Trapping Rain Water

---

💬 문제

[문제 링크]

각 칸의 높이를 나타내는 정수 배열 height
넓이는 각 1일 때 물이 고이는 칸의 넓이를 반환

✍️ 나의 풀이

/**
 * @param {number[]} height
 * @return {number}
 */
var trap = function(height) {
    let leftArray = new Array(height.length);
    let rightArray = new Array(height.lenght);

    let max = 0;
    for (let i = 0; i < height.length; i++) {
        max = max < height[i] ? height[i] : max;
        leftArray[i] = max;
    }

    max = 0;
    for (let i = height.length - 1; i >= 0; i--) {
        max = max < height[i] ? height[i] : max;
        rightArray[i] = max;
    }

    let res = 0;
    for (let i = 0; i < height.length; i++) {
        res += Math.min(leftArray[i], rightArray[i]) - height[i];
    }

    return res;
};

왼쪽에서부터 돌면서 현재에서 가장 높은 값을 새 배열에 저장
다음은 똑같이 오른쪽에서부터 돌면서 다른 배열에 저장
이후 인덱스별로 돌면서 두 배열 중 더 작은 값에서 본인의 높이를 뺀 값을 합함

📌 결과

Accepted
Runtime 73ms (Beats 20.67%)
Memory 53.66MB (Beats 20.78%)

📚 러닝 포인트

알고리즘 문제를 푼다고 하면 자주 보는 문제였다. 그래서 공략하는 방법이 있을 거라고 생각은 했는데 도저히 기억이 안나서 그림을 그려가면서 파악을 시작했다. 우선 한 번의 순회로는 알 수 없고, 왼쪽에서 한번 접근하고 오른쪽에서 한번 접근해야 한다는 힌트를 얻었다. 현재 인덱스를 기준으로 더 큰 값을 만날 때까지 물이 고인다고 생각한다. 양 끝이 가장 높다면 그게 답이 될테지만 그렇지 않은 경우에는 더 큰 값을 못만났을 때 물이 얼마나 고일지 예상할 수 없다. 그래서 반대로도 계산을 구한다. (산 같은 형태일 경우를 생각하자) 그리고 당연히 둘 중 더 낮은 높이를 기준으로 물이 고일 것이다. 거기에 본인의 높이를 빼면 고인 물의 면적을 계산할 수 있다.

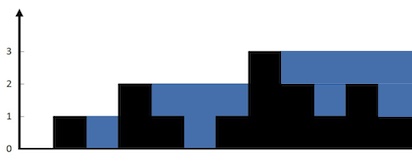
위에가 왼쪽부터 계산, 밑에가 오른쪽부터 계산했을 때의 예상도라고 생각하면 된다. 실제는 둘 중 더 낮은 높이를 기준으로 물이 고인다.