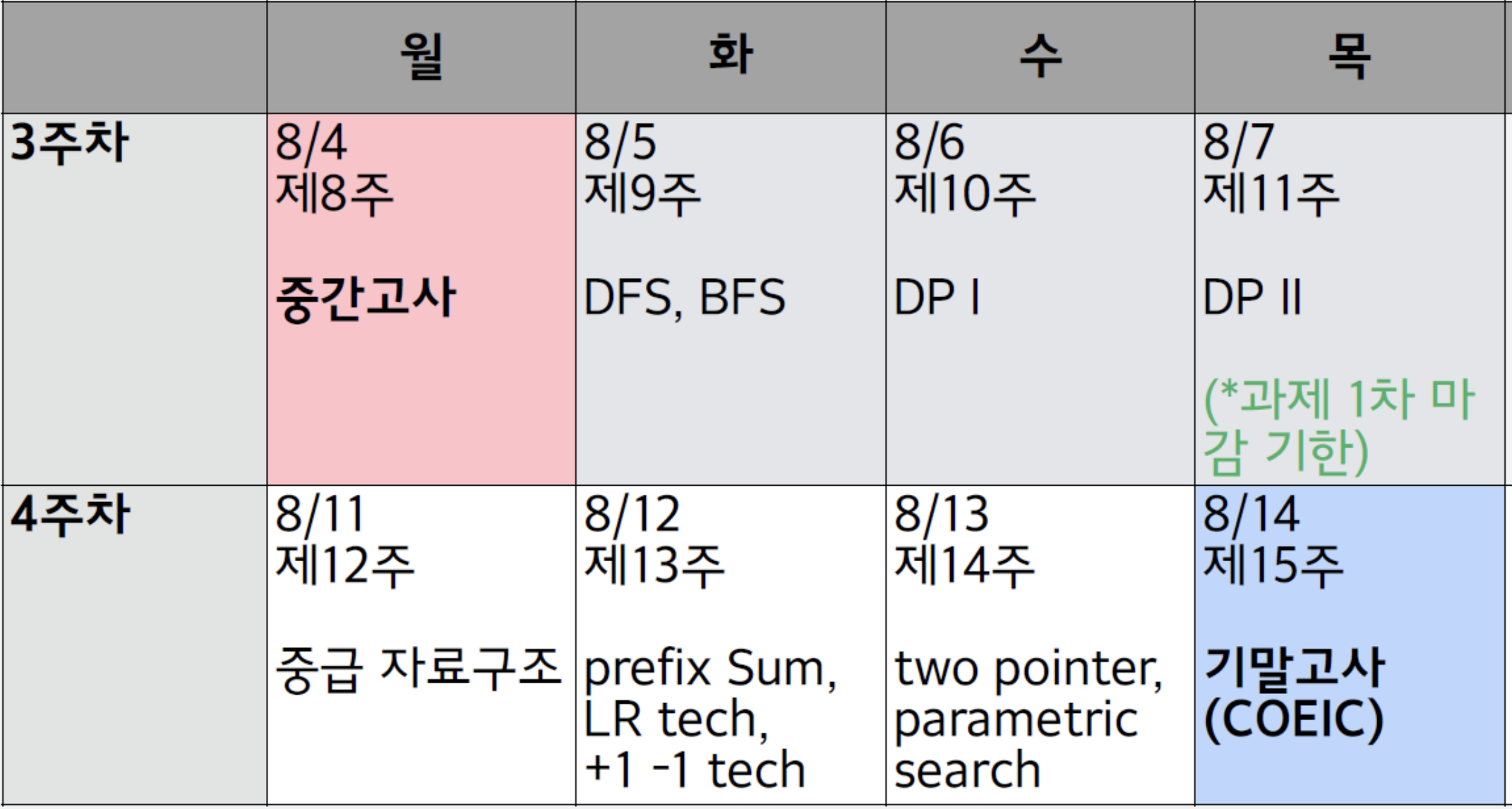
이랬는데 중간 범위 까지 나오면 나 미쳐.
DFS
DFS는 뭐게용.
깊이 우선 탐색이죠?
DFS는 보통 재귀로 구현을 많이 합니다.
나랑 연결되어 있는 그래프로... 그냥 이동을 함.
그리고 또 있으면 또 연결을 함.
그렇게 재귀를 돌다 보면 연결된 모든 노드를 방문 할 수 있다...
그치만? 파이썬에서 재귀 깊이 제한이 걸릴 수도 있으니
impory sys에
sys.setmaxrecursionlimit인가?
아니네요 sys.setrecursionlimit이네요
기본 재귀 깊이 제한은 1000입니다.
근데 경험상, 재귀 깊이 제한이 걸리면 보통 dfs로 푸는게 아니더라 ㅋㅋ
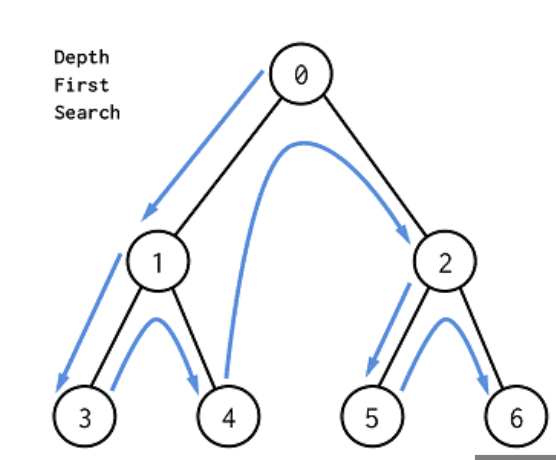
이 그림을 보면 아! 왜 깊이 우선이구나! 가 딱 느낌이 옵니다 그쳐
간단하게 예시문제 하나 풀어볼게요.
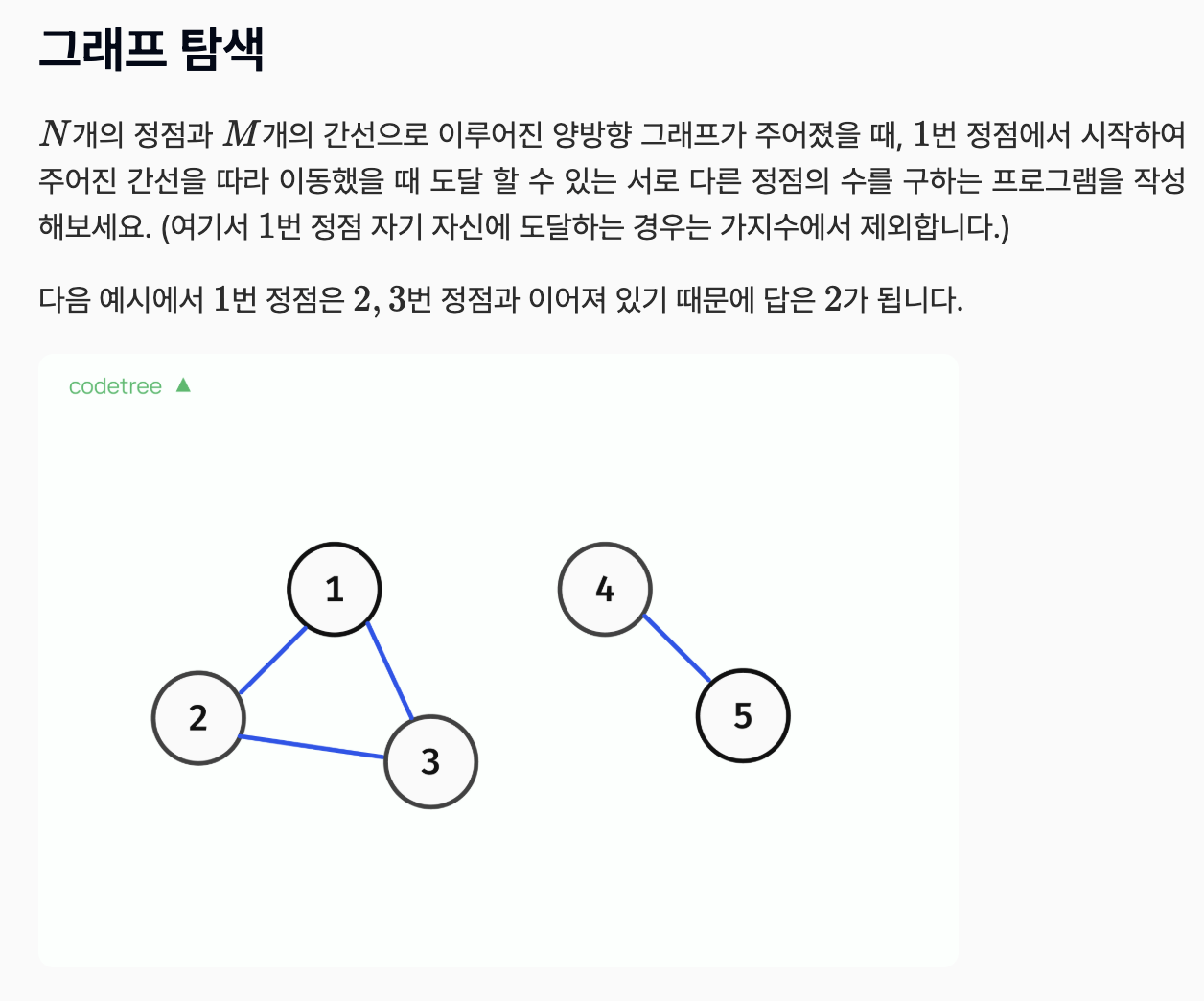
시작하는 정점이 1번으로 고정이 되어있네요
그럼 1번 정점 위치에서 DFS를 돌려서 visited한 정점의 수를 출력하면 될 거 같아요 그쵸
n,m=map(int,input().split())
ary=[[]for _ in range(n) for _ in range(n+1)]
visited=[False for _ in range(n+1)]
for i in range(m):
v1,v2=map(int,input().split())
ary[v1].append(v2)
ary[v2].append(v1)
cnt=0
def dfs(node):
global cnt
visited[node]=True
cnt+=1
for i in ary[node]:
if not visited[i]:
dfs(i)
dfs(1)
print(cnt-1)
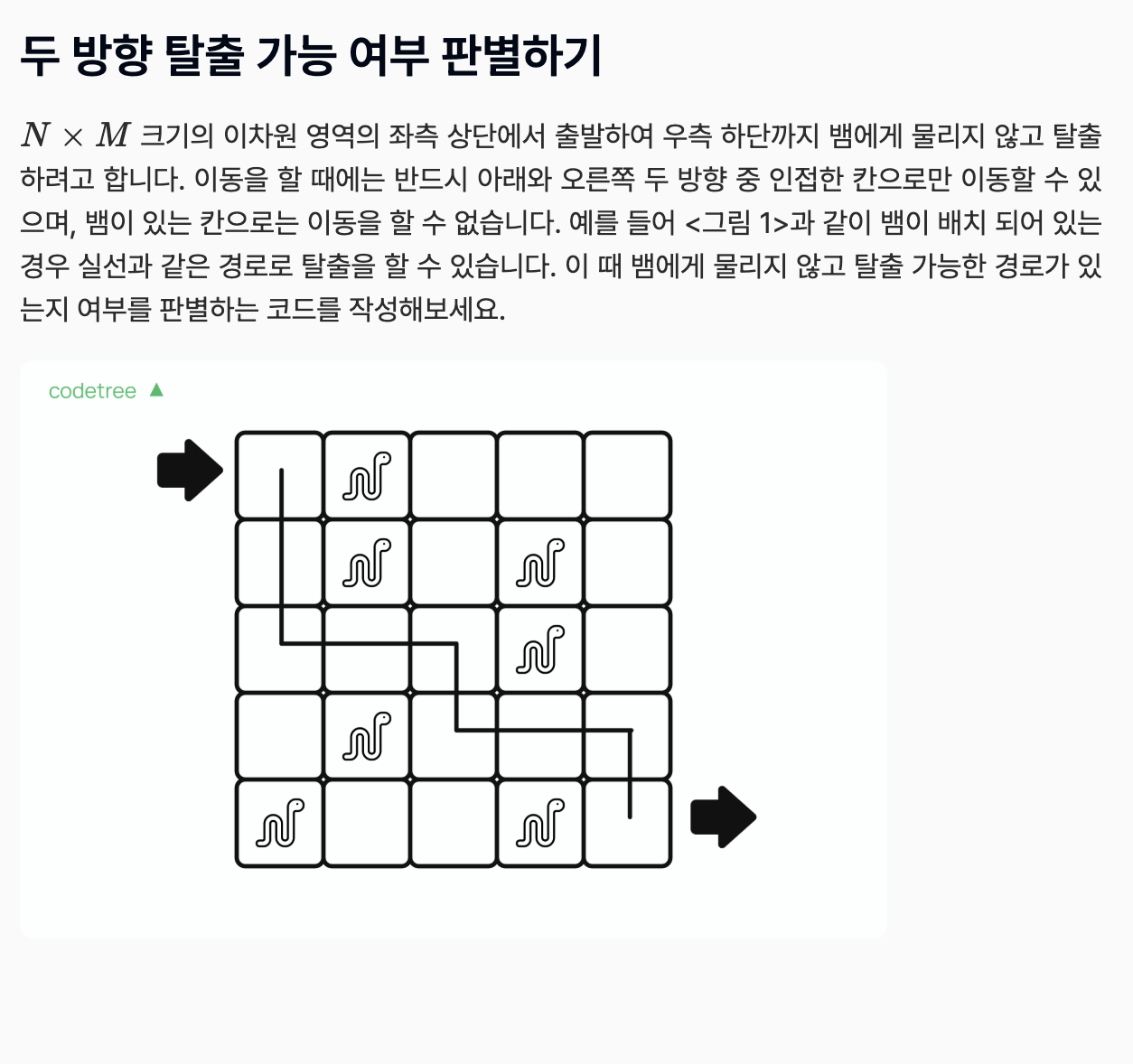
n,m=map(int,input().split())
ary=[list(map(int,input().split())) for _ in range(n)]
visited=[[False for _ in range(m)] for _ in range(n)]
dx=[0,1]
dy=[1,0]
def check(y,x):
if 0<=y<n and 0<=x<m and ary[y][x]==1:
return True
return False
def dfs(y,x):
visited[y][x]=True
for i in range(2):
ty=y+dy[i]
tx=x+dx[i]
if check(ty,tx) and not visited[ty][tx]:
dfs(ty,tx)
dfs(0,0)
if visited[n-1][m-1]:
print(1)
else:
print(0)네 방향인 줄 알고 하다 왜 틀렸지 했다...
BFS
BFS는 넓이 우선 탐색이다.
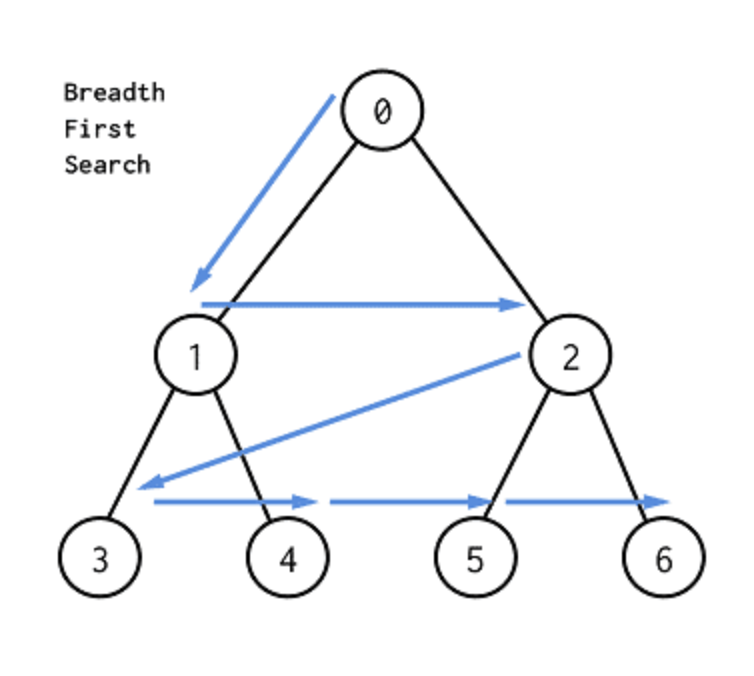
그렇다 넓이 우선이다.
얘는 어떻게 구현을 하냐?
큐를 쓰면 된다.
나랑 연결된 노드를 큐에 넣고,
방문하고, 큐에 넣고
그런 식이다.
아 그리고 ! "최단 경로" 이게 나오면 거의 반드시 BFS로 푸는 문제라 했다.
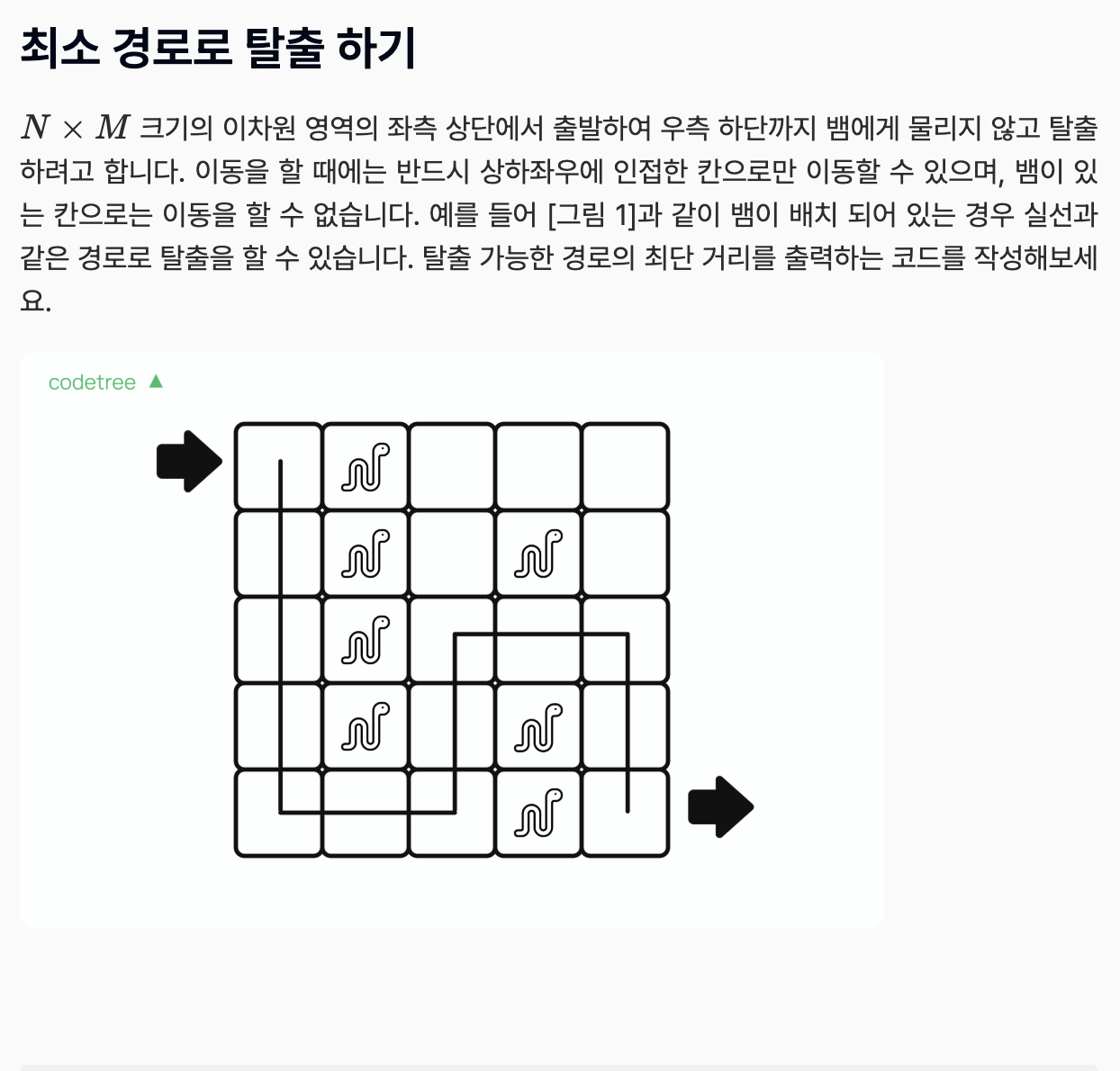
from collections import deque
n,m=map(int,input().split())
ary=[list(map(int,input().split())) for _ in range(n)]
visited=[[False for _ in range(m)]for _ in range(n)]
dx=[0,1,0,-1]
dy=[-1,0,1,0]
q=deque()
q.append((0,0,0))
def check(y,x):
if 0<=y<n and 0<=x<m and ary[y][x]==1 and not visited[y][x]:
return True
return False
while q:
y,x,c=q.popleft()
if y==n-1 and x==m-1:
print(c)
for i in range(4):
ty=y+dy[i]
tx=x+dx[i]
if check(ty,tx):
visited[ty][tx]=True
q.append((ty,tx,c+1))
visited[0][0]=True
if not visited[n-1][m-1]:
print(-1)DP
DP를 그동안 많이 안 풀기도 했고 좀 어려워 하기도 했는데, 수업을 들으면서 많이 도움이 됐다.
결국은 상태 정의를 어떻게 내리는 지가 중요하다.
점화식이라는 걸 결국 이 식이 어느 상태에 들어가도 성립을 해야하는 것이다.
초기 상태를 잘 정하고, 특정 상황에 어느 수가 들어가도, 그 앞에 어느 값이 왔던 동일한 상황처럼 만드는 점화식을 뽑아내면 되는것이다.

피보나치 수의 점화식은
dp[i]=dp[i-1]+d[i-2] 단 i>=2다.
그렇다면 dp[0]에 1 dp[1]에 1을 넣고 반복문을 돌린다면
O(N)에 값을 구할 수 있는 것.


그럼 이건 어떻게 할 것이냐...?
생각을 좀 해보자... 이 친구의 상태 정리를 어떻게 내리는게 좋을까?
dp[y][x]라고 생각해보자.
dp[y][x]는 dp[y-1][x]와 dp[y-1][x-1]에 따라 정해지지 않을까?
그럼 dp의 초기 상태를 어떻게 정해주면 될까?
dp[0~n][0]의 값은 정해져 있지 않나? 왜냐면 이동을 하단으로만 하는 경우니까.
그럼 마찬가지로 우측하단대각선으로 이동하는 경우에도 값은 정해져있다.
그럼 이제 남은 값은 하단이동과 우측하단 대각선 이동을 제외하고 남은 값인데,
이 경우에는 dp[y-1][x]와 dp[y-1][x-1]을 비교해서 더 큰 애를 넣어주면 된다.

이건 어떻게 하면 될까?
마찬가지로 초기 값을 정해주고,
점화식을 조금만 다르게 해주면 된다.
대각선 이동이 안되니, dp[y-1][x]와 dp[y][x-1]을 비교하면 되지 않을까?
n=int(input())
ary=[list(map(int,input().split()))for _ in range(n)]
dp=[[0 for _ in range(n)]for _ in range(n)]
dp[0][0]=ary[0][0]
for v in range(1,n):
dp[v][0]=dp[v-1][0]+ary[v][0]
dp[0][v]=dp[0][v-1]+ary[0][v]
for y in range(1,n):
for x in range(1,n):
dp[y][x]=max(dp[y-1][x]+ary[y][x],dp[y][x-1]+ary[y][x])
print(dp[n-1][n-1])
이 문제는 어떻게 해야할까?
상태 정의를 해보자. 내가 고른 원소와, 원소의 위치를 알고 있으면 된다.
그럼 dp[i]의 정의를 i는 위치, 그리고 dp[i]는 지금까지 수열의 길이로 정의를 해보자.
dp[0]=1
dp[i]는 ary[j] < ary[i]인 경우에 값을 비교하여 dp[j]+1 과 dp[i]중에 큰 값을 넣음 된다.
n=int(input())
ary=list(map(int,input().split()))
dp=[1 for _ in range(n)]
for i in range(n):
for j in range(i):
if ary[j]<ary[i]:
dp[i]=max(dp[i],dp[j]+1)
rs=max(dp)
print(rs)
ㅠㅠ 다시봤는데도 답이 뚝딱 생각이 안 나네

얜 이 동전으로 만들 수 있는 수를 dp에 저장해두고, 그 수를 만드는데 필요한 최소의 동전의 수를 dp에 값으로 넣으면 될 거 같다. 동의 하시는지?
예를 들어 문제의 예시로 1,4,5의 동전의 경우에
dp[1,4,5]는 1이다.
그럼 dp[2]는? 2다
1+1로 밖에 못 만드니까
그럼 dp[3]은? dp[2]+dp[1]이다.
n,m=map(int,input().split())
ary=list(map(int,input().split()))
dp=[10001 for _ in range(m+1)]
dp[0]=0
for i in range(m+1):
for j in range(n):
if i-ary[j]>=0 and not dp[i-ary[j]]==10001:
dp[i]=min(dp[i],dp[i-ary[j]]+1)
if dp[m]==10001:
print(-1)
else :
print(dp[m])
사실 전에 이 문제를 풀었을 땐 미리 dp에 가지고 있는 동전의 수에 맞게 1을 최소의 수로 넣고 풀었는데, 굳이 그럴 필요가 없고 dp[0]=0을 넣어주면 상관이 없어진다.
그리고 이후에 나오는 문제가 이 방식을 뒤집어서 하는 경우
각 동전을 최소로 사용해서 수열을 채우는 문제를 해결 할 수 있다.

n, m = map(int, input().split())
ary = list(map(int, input().split()))
# Please write your code here.
dp=[99999999 for _ in range(m+1)]
dp[0]=0
for i in range(n):
for j in range(m,-1,-1):
if j >= ary[i]:
if dp[j-ary[i]]==99999999:
continue
dp[j]=min(dp[j],dp[j-ary[i]]+1)
if dp[m]==99999999:
print(-1)
else:
print(dp[m])
그리고 이제 또... 디피가 나오는데 여긴 좀 거시기하다.
여긴 나중에 알아보도록 하자. 아니 왜냐면 하루종일 문제 풀었는데 두 개 풀었었거든...
hash 기본

걍 딕셔너리다. 좀 쓸만했던건 딕셔너리에 .get(value,default)이런 식으로 값을 가져오고 없다면 default를 반환하는 문법 정도를 기억하자.

얜 set이다. append대신 add pop대신 remove를 사용한다.

n = int(input())
ar1=list(map(int,input().split()))
m=int(input())
ar2=list(map(int,input().split()))
s1=set(ar1)
for i in ar2:
if i in s1:
print("1",end=" ")
else:
print("0",end=" ")
그니까 이런 식으로 활용이 가능하다.

이제 우선순위큐가 조금 유용하면서도 복습을 해줘야하는 부분인데,
우선순위큐는 우선순위에 맞게 큐가 정리가 된다.
파이썬에서는 heapq로 사용을 할 수 있고, 얘는 min-heap이다.
그니까 최상위 노드에 min 값이 오는 거임 ㅇㅇ
그리고 이해를 조금 해주면 좋은게, heapq는 파이썬의 list를 우선순위큐로 사용할 수 있게 해주는거다. 그러니까 list를 내가 직접 조작하면 heapq가 만들어둔 우선순위큐의 신뢰도가 없어지겠지? 그러지말자.
import heapq를 해주고
heapq.heappush(list,value)
이런 식이었던 거 같은데
맞다 ㅇㅇ 사실 이것만 알면 된다
heappop정도?

그럼 이제 이런 것도 걍 풀 수 있다.

아 그리고 우선순위큐에 tuple로 값을 넣으면 지 알아서 인자 순서대로 값을 확인해서 정렬을 해준다. 만약에 정렬해야하는 기준값이 있다면 튜플로 넣고, 순서를 신경을 써주자.
그리고 13일차...
디피 비슷한 거 하나 나오고...
누적합이라는데, 디피랑 차이점을 잘 모르겠다. 디피를 잘 쪼개면 이런 개념도 나오나보다.

이 문제는 결국 또 상태 정의를 어케 할래? 인데
dp[y][x]까지의 합을 다 정하면 된다.
그리고, 반복을 돌면서 k*k 크기의 최대 넓이를 찾으면 된다. 빼고 더하고 뭐 해주면 되겠죠?
n, k = map(int, input().split())
arr = [[0 for _ in range(n+1)]]+[[0]+list(map(int, input().split())) for _ in range(n)]
dp=[[0 for _ in range(n+1)]for _ in range(n+1)]
for y in range(1,n+1):
for x in range(1,n+1):
dp[y][x]=dp[y-1][x]+dp[y][x-1]+arr[y][x]-dp[y-1][x-1]
value=0
for y in range(k,n+1):
for x in range(k,n+1):
value=max(value,(dp[y][x]+dp[y-k][x-k]-dp[y-k][x]-dp[y][x-k]))
print(value)

이건 완벽하게 습득하지 못했으니 알아보자.

어케 할래?
흠... 얘도 결국 dp 처럼 생겼다.
근데 제외를 하란다.
살짝 이전 시간에 공부를 했던 지식으로 생각을 해보면
제외하는 값 기준 왼쪽 dp 값과 오른쪽 dp 값을 알고 있으면
풀 수 있다 했다. 왜 그럴까?
일단 띵킹을 해보자.
[3,6,2,6,7,5,2]
의 경우에서 7을 제외하기전엔,
3 + 4 + 4 + 1 + 2+ 3 = 17이다.
7을 제외하면?
3 + 4 + 4 + 1 + 3 =15다.
그럼 dp의 상태 정의를 어떻게 할까 ?
dp는 결국 지금까지의 상태를 연속해서 저장해두는 것이다.
근데, 중간에 값을 제외시키면 "연속성"이 사라지게 된다.
그럼 dp가 의미가 없다.
오 그럼 dp를 왼쪽에서의 합과 오른쪽에서의 합으로 정리를 해보자.
그럼 ldp는
3,7,11,12,14,17
rdp는
3,5,6,10,14,17
이다
그럼 7을 제외 시키는 경우면, 배열의 5번째 값을 없애는 것, 그렇다면 dp에서는
4번째 값과 5번째 값에 영향을 준다.
rdp의 경우에는 2번째와 3번째 값에 영향을 받는다.
그렇다면 12,14와 5과 6에 문제가 있다.
근데 이렇게 보면 이해하기 힘드니까
3,7,11,(12,14),17
17,14,10,(6,5),3
이렇게 보자.ldp[2]까진 써먹을 수 있는 값이고,
rdp[0]까지는 멀정한 값이다.
rdp[0]은 |ary[5]-arr[4]|
ldp[2]는 |ary[0]-arr[1]| + |arr[1]-arr[2]| + |arr[2]-arr[3]|
ldp[3]은 ldp[2]+|arr[3]-arr[4]| 이고
rdp[1]은 rdp[0]+|arr[3]-arr[4]|
이다. 근데 7을 빼면
|ary[3]-arr[5]|
이 값이 필요하다.
그럼 ldp와 rdp의 쓸 수 있는 값은 쓰고 저 값은 구해서 넣어주면 된다.
딱 알았으.

import sys
INT_MAX = sys.maxsize
# 변수 선언 및 입력:
n = int(input())
x, y = [], []
L, R = [0] * n, [0] * n
ans = INT_MAX
# n개의 점 입력
for _ in range(n):
given_x, given_y = tuple(map(int, input().split()))
x.append(given_x)
y.append(given_y)
# L 배열을 채워줍니다.
# L[i] = 0번부터 i번까지 빠지는 부분 없이
# 순서대로 방문하기 위해
# 이동해야 하는 거리의 합
L[0] = 0
for i in range(1, n):
L[i] = L[i - 1] + abs(x[i] - x[i - 1]) + abs(y[i] - y[i - 1])
# R 배열을 채워줍니다.
# R[i] = i번부터 n - 1번까지 빠지는 부분 없이
# 순서대로 방문하기 위해
# 이동해야 하는 거리의 합
R[n - 1] = 0
for i in range(n - 2, -1, -1):
R[i] = R[i + 1] + abs(x[i + 1] - x[i]) + abs(y[i + 1] - y[i])
# 각 체크포인트 마다
# 건너 뛰었다고 했을 때,
# 가능한 거리 합 중 최솟값을 계산합니다.
for i in range(1, n - 1):
ans = min(ans, L[i - 1] + R[i + 1] + abs(x[i + 1] - x[i - 1]) + abs(y[i + 1] - y[i - 1]))
print(ans)
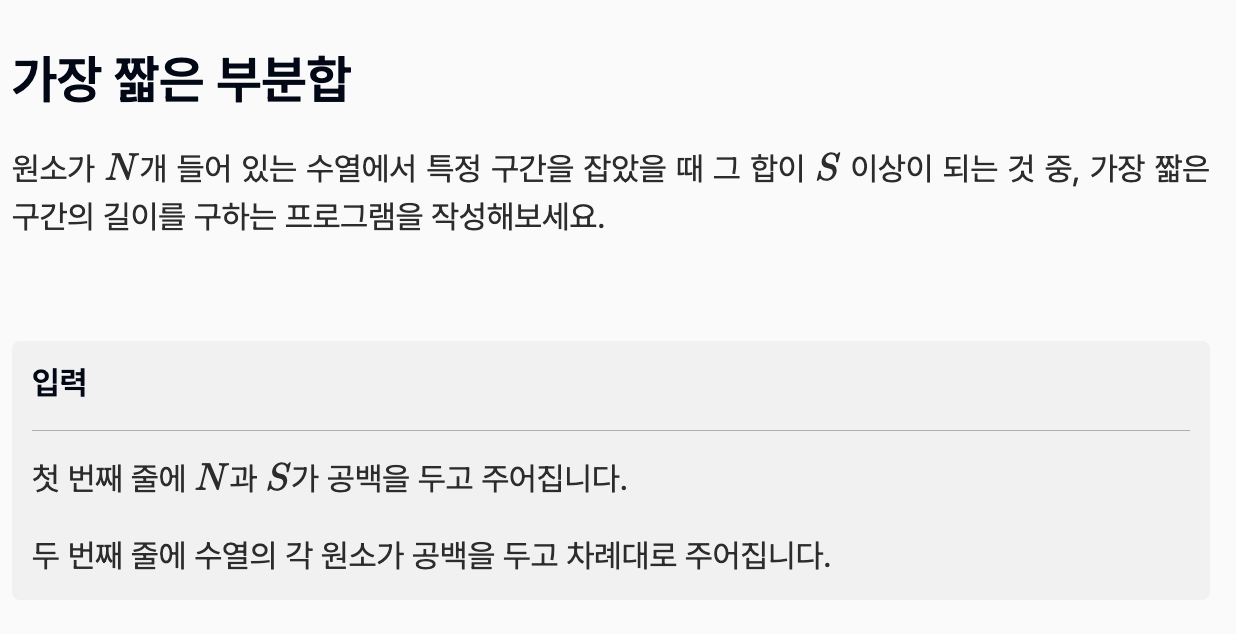
이건 투포인터다.
n, s = map(int, input().split())
arr = list(map(int, input().split()))
left = 0
window_sum = 0
min_length = float('inf')
for right in range(n):
window_sum += arr[right]
while window_sum >= s:
min_length = min(min_length, right - left + 1)
window_sum -= arr[left]
left += 1
if min_length == float('inf'):
print(-1)
else:
print(min_length)for 문을 돌리고, 그 안에서 while로 투 포인터를 돌리는 걸 잊지 말자

# 변수 선언 및 입력:
n, m = tuple(map(int, input().split()))
A = [0] + list(map(int, input().split()))
B = [0] + list(map(int, input().split()))
def is_subsequence():
i = 1
# B의 원소를 기준으로
# 순서대로 매칭이 가능한지를 확인합니다.
for j in range(1, m + 1):
# A의 원소가 B의 j번째 원소와
# 일치해지는 위치를 구해줍니다.
while i <= n and A[i] != B[j]:
i += 1
# 만약 수열 A에서 일치하는 원소를 찾지 못햇다면
# 부분수열이 아닙니다.
if i == n + 1:
return False
# 일치한다면
# A 원소의 위치도 한칸 앞으로 이동시켜 줍니다.
else:
i += 1
# 전부 매칭하는게 가능했다면
# 부분수열입니다.
return True
# 부분수열이라면 Yes를 출력합니다.
if is_subsequence():
print("Yes")
else:
print("No")
Parametric Search

이건 설명해주실 때 나무 예시를 들으셨는데...
잘 이해를 못했어서 그냥 코드트리에 있는 글로 이해를 해보겠다.

이게 문제인데,
결국은 답이 될 수 있는 범위 내에서 이진탐색으로 답을 찾는 방법이다.
ㅇㅇ...

그럼 이건 어떻게 풀까?
N으로 K를 M개 만들어야한다.
그렇다는건 K가 될 수 있는 최소의 수와 최대의 수가 나올 것이고,
이진 탐색으로 K의 수를 찾으면 될 것 이다.
n, m = map(int, input().split())
arr = [int(input()) for _ in range(n)]
# Please write your code here.
max_num=sum(arr)
min_num=1
def is_possible(num):
ct=0
for i in arr:
ct+=i//num
if ct >= m:
return True
else:
return False
rs=0
while min_num<max_num:
mid=(min_num+max_num)//2
if is_possible(mid):
rs=max(rs,mid)
min_num=mid+1
else:
max_num=mid
print(rs)
이해완.
이제 다 할 줄 아는 거 같다...
잘 하기만 하면 된다...
