#1504

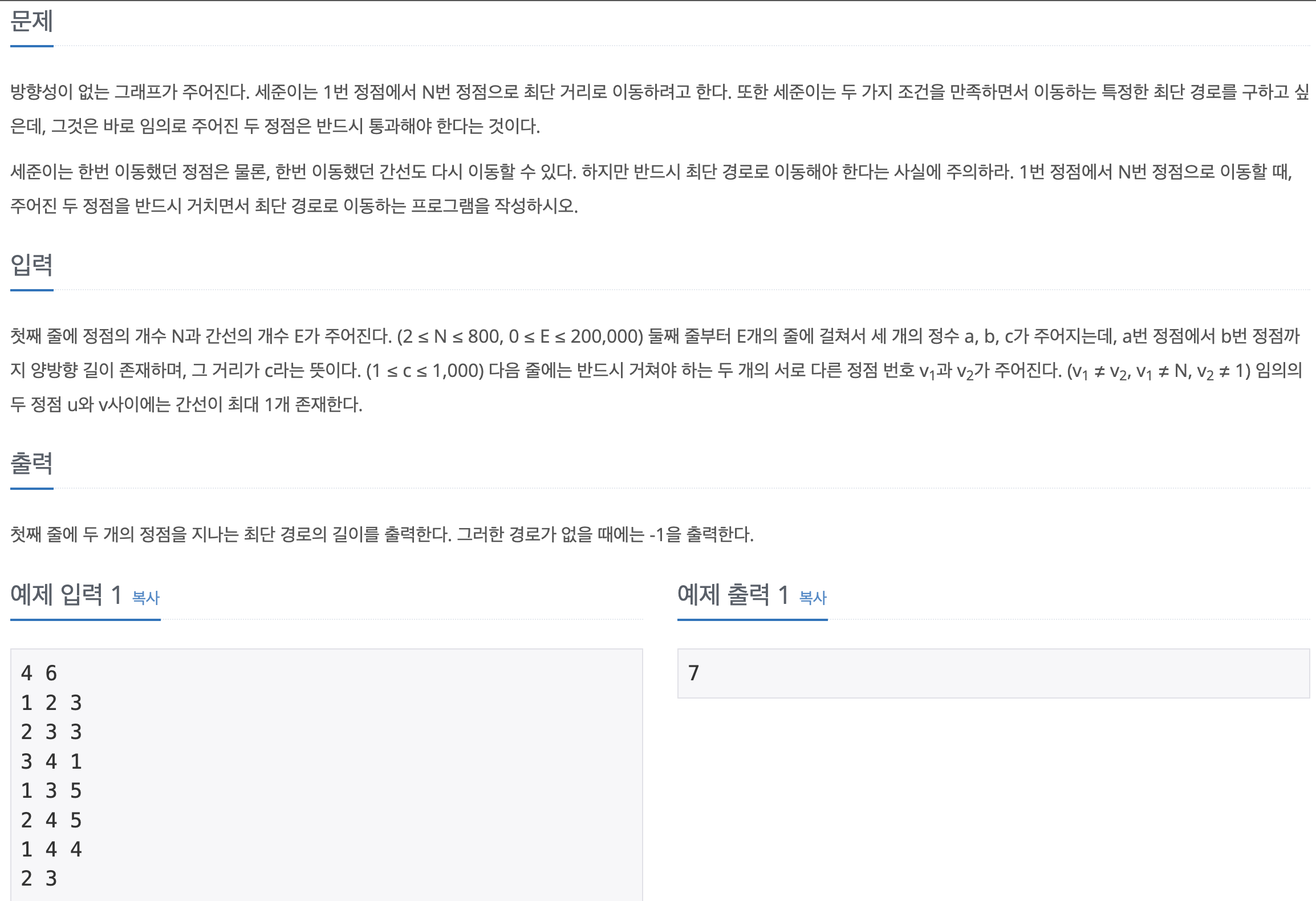
이전에 풀었던 최단거리 문제와 비슷하다. 다익스트라 알고리즘을 이용하여 시작노드부터 도착노드까지의 최단거리를 구하는데, 꼭 지나야 하는 두 노드가 있다는 조건이다.

방법은 간단하다.

2번 노드와 3번 노드를 거쳐서 가야한다면 2가지 경우밖에 안나온다는 점을 이용한다.

1. 1번 노드에서 출발 -> 2번 노드 지나서 -> 3번 노드 지나서 -> 도착노드 도착
2. 1번 노드에서 출발 -> 3번 노드 지나서 -> 2번 노드 지나서 -> 도착노드 도착

2가지 경우를 모두 구해주고 최소값을 구해주면 된다.

import heapq 
import sys
input = sys.stdin.readline

N, M = map(int, input().split())
inputGraph = [[] for _ in range(N+1)]

for _ in range(M):
    a, b, c = map(int, input().split())
    inputGraph[b].append((a,c))
    inputGraph[a].append((b,c))
    # a부터 b까지 다이렉트로 비용은 c
    # graph[b] = (a,c)
    # 반대로도 넣어줘야 함

V1, V2 = map(int, input().split())
# print(graph)

inf = sys.maxsize

def dijkstra(start):
    distance_table = [inf for _ in range(N+1)]
    # N이 4면 => [inf, inf, inf, inf, inf]
    distance_table[start] = 0
    # 출발 지점에서 거리는 0

    heap = []
    heapq.heappush(heap, (0, start))
    # 출발지점에서 거리는 0

    while heap:
        # 빌 때까지 반복

        dist, nowNode = heapq.heappop(heap)
        # 거리가 가장 짧은 노드 빼와서 계산 시작

        for node in inputGraph[nowNode]:
            #현재 노드와 인접한 노드들을 확인
            cost = node[1] + dist

            if cost < distance_table[node[0]]:
            # cost(다른 노드들 거쳐서 왔을 때의 비용)와 start에서의 다이렉트 거리를 비교
                distance_table[node[0]] = cost
                heapq.heappush(heap, (cost, node[0]))

    return distance_table

one_table = dijkstra(1)
V1_table = dijkstra(V1)
V2_table = dijkstra(V2)

answer1 = one_table[V1] + V1_table[V2] + V2_table[N]
answer2 = one_table[V2] + V2_table[V1] + V1_table[N]

cnt = min(answer1, answer2)
print(cnt if cnt < inf else -1)

팁 1 - 다익스트라 풀 때 무한대로 거리 테이블 초기화 해야 하는데 이 때

inf = sys.maxsize

팁 2 - 마지막 정답 출력할 때 2가지 경우에서의 최소값을 출력하고 해당이 안될 경우 -1을 출력하라는 경우가 가끔 있는데 이 때

print(cnt if cnt < inf else -1)

팁 3 - 다익스트라 폼 코드 그대로 백지에 손코딩으로 다 적을 수 있을 때까지 그냥 완전히 갖다 외워버리기 => 변수명도 계속 쓸거니까 고대로 외워서 쓰기