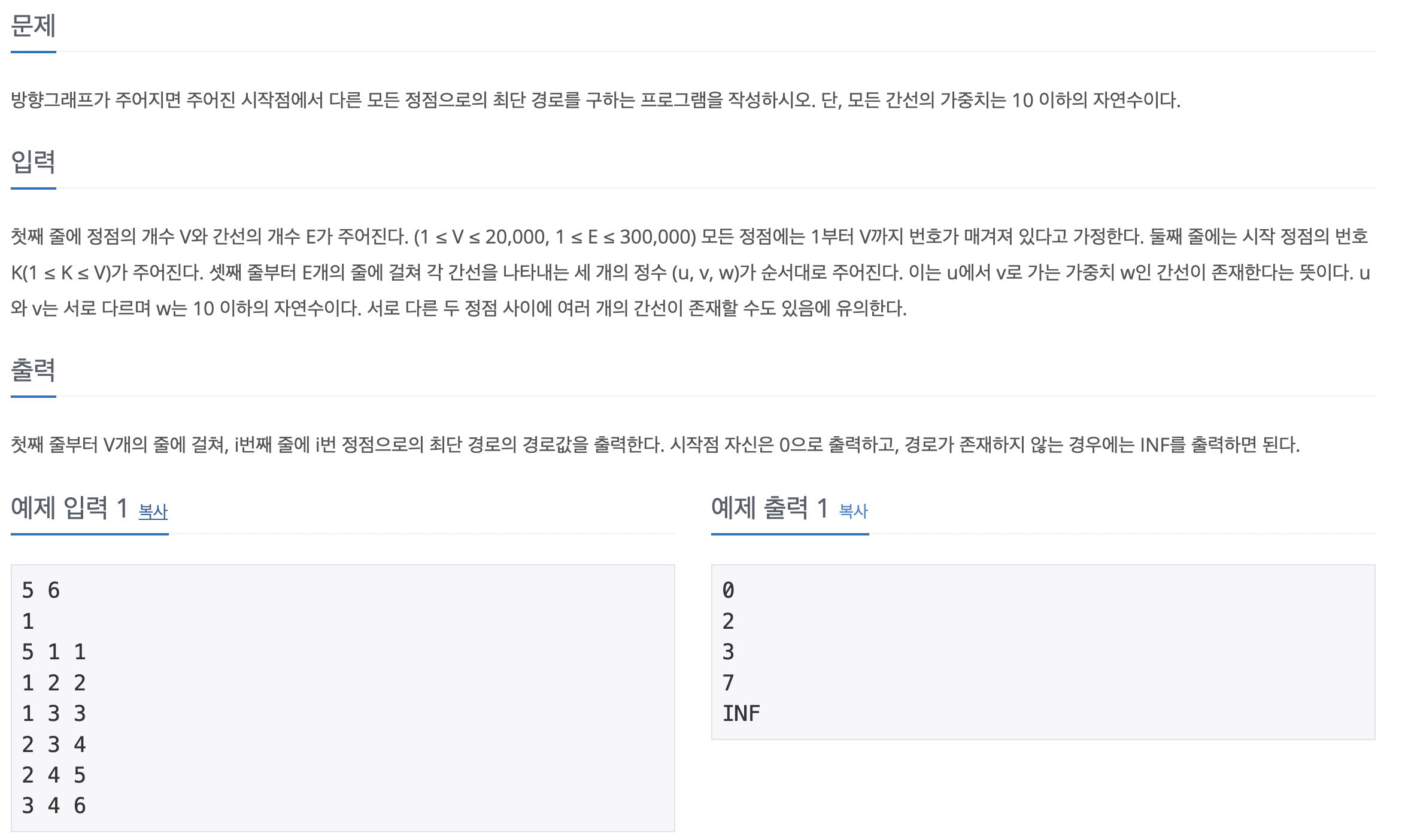
시작 노드가 주어졌을 때 각 노드까지의 최단거리를 구하는 문제이다.
다익스트라를 적용하는 문제로 가장 기본적인 문제이다.
(벌써 최단거리까지 왔다니.. 괴물 신인의 등장)
이전에 리트코드 책으로 파이썬 알고리즘을 공부했었는데 전부 까먹어서.. 구글링 다시 하면서 프린트도 하나씩 찍어보고 전부 정리해가면서 문제를 풀어봤다.
첫 번째 풀이
첫 번째로 완전 정석대로 풀어봤다.
import sys
input = sys.stdin.readline
# 꿀팁 1 - 이렇게 하면 굳이 귀찮다고 안하는게 아니라 평소처럼 하는데 시간은 조금이나마 주는거잖아?
INF = int(1e9)
# 꿀팁 2 - 양의 무한대
N, M = map(int, input().split())
startNode = int(input())
# 주어지는 그래프 정보 담는 N개 길이의 리스트
graph = [[] for _ in range(N+1)]
visited = [False] * (N+1) # 방문처리 기록용
distance = [INF] * (N+1) # 거리 테이블용
for _ in range(M):
u, v, w = map(int, input().split())
# 출발 노드 : u
# 도착 노드 : v
# 간선 비용 : w
graph[u].append((v, w))
# 튜플로 묶어서 리스트의 값으로 넣어준다.
print("graph = ", graph, "\n")
# 방문하지 않은 노드이면서 시작노드와 최단거리인 노드 반환
def get_smallest_node():
min_value = INF
index = 0
for i in range(1, N+1):
# 1 부터 N까지 전부 다 방문할거야 => 순차 탐색
# => 시간초과가 나오는 이유
# => 우선순위 큐를 써서 풀어야 하는 이유
if not visited[i] and distance[i] < min_value:
min_value = distance[i]
index = i
print(" 안가본 노드 중에 가장 최단 거리의 노드는 ? ", index , "\n")
return index
# 다익스트라 알고리즘
def dijkstra(start):
# 시작노드 -> 시작노드 거리 계산 및 방문처리
distance[start] = 0
visited[start] = True
# 시작노드의 인접한 노드들에 대해 최단거리 계산
for node in graph[start]:
distance[node[0]] = node[1]
# 시작노드 제외한 n-1개의 다른 노드들 처리
for _ in range(N-1):
# n=5, 노드가 5개면 4번 돌겠지
now = get_smallest_node()
# now => 방문안했으면서 시작노드와 최단거리인 노드
visited[now] = True
# 해당 노드 방문처리
print("now = ", now, " 방문 처리 " , "\n")
# 해당 노드의 인접한 노드들 간의 거리 계산
for next in graph[now]:
print(now, " 에서 출발할 수 있는 노드 next = ", next , "\n")
cost = distance[now] + next[1]
print("cost = ", cost, " = ", now, " 까지 오는 최단거리 : ",distance[now] ,"+ ", next[0]," 까지 오는데 비용 : ", next[1] , "\n")
# 시작->now 거리 + now->now의 인접노드 거리
if cost < distance[next[0]]: # cost < 시작->now의 인접노드 다이렉트 거리
distance[next[0]] = cost
dijkstra(startNode)
for i in range(1, N+1):
if distance[i] == INF:
print("INF")
else:
print(distance[i])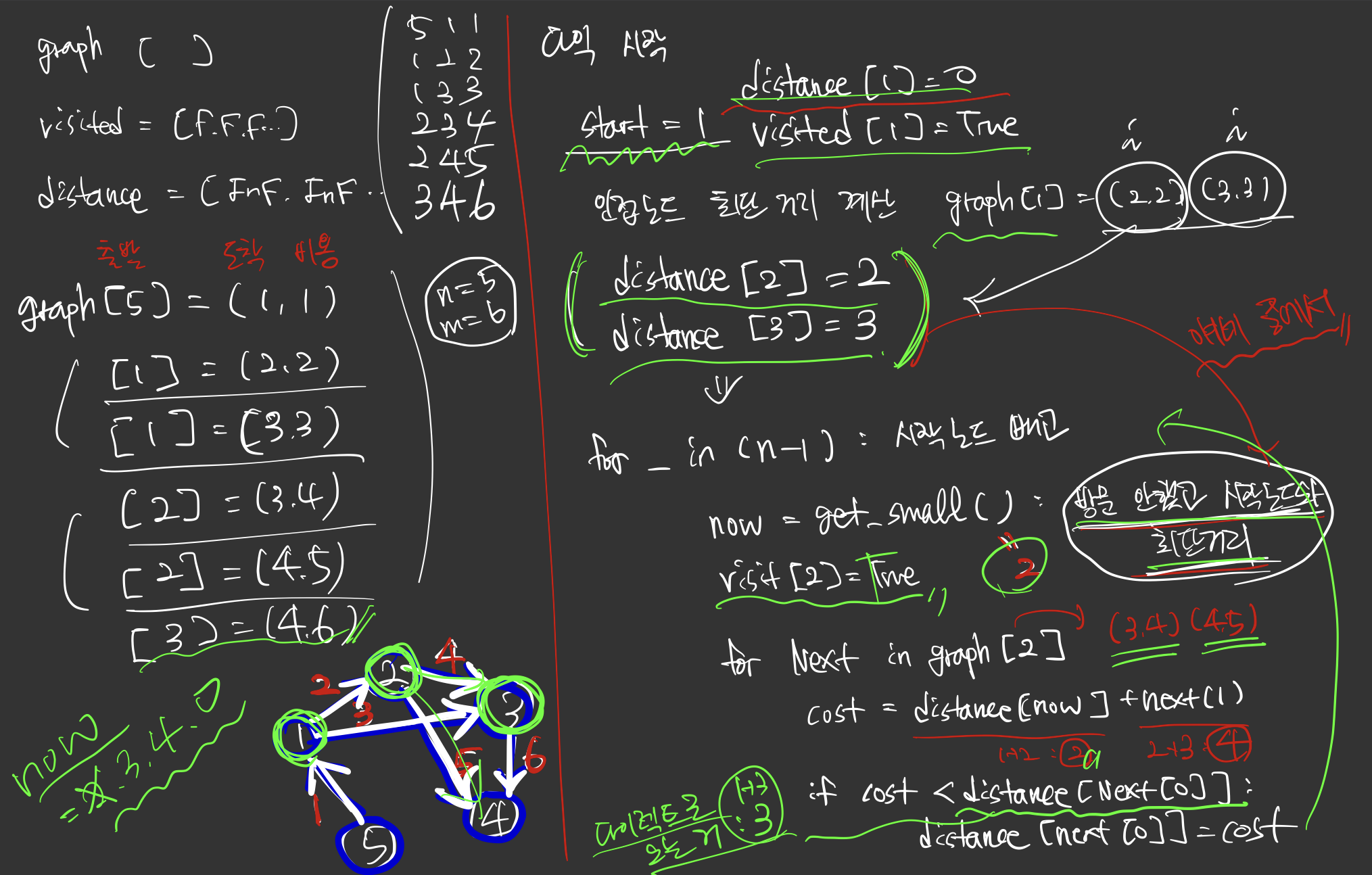
입력이 테스트 케이스 1과 같이 주어졌을 때 흐름은 아래와 같다.
Test Case 1 Input
5 6
1
5 1 1
1 2 2
1 3 3
2 3 4
2 4 5
3 4 6
정답은 맞지만 시간초과가 뜬다. 위와 같은 풀이를 간단한 다익스트라 풀이라고 하더라
간단한 다익스트라 알고리즘은 V가 노드의 개수라고 가정할 때, 시간 복잡도가 O(V^2) 이다. 왜냐하면 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하기 위해 매 단계마다 모든 노드(1차원 테이블을 순차 탐색)를 돌아봐야 하기 때문이다.
대략적으로 계산해봤을 때 노드의 개수가 5000개 이하이면 위의 풀이로도 풀린다. 하지만 그 이상인 경우엔 시간초과가 뜬다.
( 이 문제의 주어진 조건
=> 첫째 줄에 정점의 개수 V ~~ (1 ≤ V ≤ 20,000)
=> 시간초과
이를 해결하기 위해 우선순위 큐를 활용한 다익스트라 풀이가 있다. 개선한 우선순위 큐 즉, heapq를 활용한 개선된 다익스트라 알고리즘이라고 한다.
스택(Stack) : 가장 나중에 삽입된 데이터 먼저 pop
큐(Queue) : 가장 먼저 삽입된 데이터 먼저 pop
우선순위 큐(Priority Queue) : 우선순위가 높은 데이터 먼저 pop
기존의 방법(간단한 다익스트라 풀이)는 최단 거리를 기록하면서 갱신할 거리 테이블, 두 번째는 방문한 노드인지 체크하는 방문 테이블, 총 2개의 테이블이 필요했다.
하지만 우선순위 큐를 이용하게 되면 최단 거리를 기록할 거리 테이블만 정의한다. 왜냐하면 우선순위 큐를 이용하게 되면 우선순위 큐가 알아서 가장 최단 거리인 노드를 가장 앞으로 정렬해주기 때문에 기존에 기록한 최단 거리보다 크다면 그냥 무시해주면 된다.
만약 기존에 기록한 최단 거리보다 더 짧은 새로운 최단 거리가 등장하게 되면 해당 거리와 노드를 우선순위 큐에 넣어준다.
두 번째 풀이
# 5 6
# 1
# 5 1 1
# 1 2 2
# 1 3 3
# 2 3 4
# 2 4 5
# 3 4 6
import heapq
import sys
input = sys.stdin.readline
# 꿀팁 1 - 이렇게 하면 굳이 귀찮다고 안하는게 아니라 평소처럼 하는데 시간은 조금이나마 주는거잖아?
INF = int(1e9)
# 꿀팁 2 - 양의 무한대
N, M = map(int, input().split())
startNode = int(input())
# 주어지는 그래프 정보 담는 N개 길이의 리스트
graph = [[] for _ in range(N+1)]
visited = [False] * (N+1) # 방문처리 기록용
distance = [INF] * (N+1) # 거리 테이블용
for _ in range(M):
u, v, w = map(int, input().split())
# 출발 노드 : u
# 도착 노드 : v
# 간선 비용 : w
graph[u].append((v, w))
# print("graph = ", graph, "\n")
# 이까진 코드 전과 동일
def dijkstra(start):
q = []
# 시작 노드로 가기 위한 최단 경로는 0을 설정하여, 큐에 삽입
heapq.heappush(q, (0, start))
distance[start] = 0
while q: # 큐가 비어있지 않으면 계속 진행
# 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
dist, now = heapq.heappop(q)
# 현재 노드가 이미 처리된 적이 있는 노드라면 무시
if distance[now] < dist:
continue
# 현재 노드와 연결된 다른 인접한 노드들을 확인
for node in graph[now]:
cost = dist + node[1]
# 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[node[0]]: # cost < 시작->now의 인접노드 다이렉트 거리
distance[node[0]] = cost
heapq.heappush(q, (cost, node[0]))
dijkstra(startNode)
for i in range(1, N+1):
if distance[i] == INF:
print("INF")
else:
print(distance[i])두 번째 풀이가 잘 이해가 안될 수 있는데 아래 강의가 되게 설명이 잘 되어있다. 참고하면 좋을 것 같다.
https://freedeveloper.tistory.com/384
풀이 2개 전부 천천히 따라가면 그렇구나 하면서 그림도 그려가면서 이해도 잘 되는데 막상 백지 놓고 다시 한번 풀어봐라 하면 또 막힌다.
이해했으면 이제 외울 차례인가
달달달 외워버리자. 위에 영상에 나온 분이 말씀해주시길
간단한 다익스트라 코드 뿐만 아니라 개선된 다익스트라 코드까지 자다가도 벌떡 일어나서 바로 구현할 수 있어야 할 정도로 반복 숙지를 해야한다.
뭐 그게 어렵나? 그냥 무지성으로 코드 통째로 외워 버리자. 언제 어디서든 쓸 수 있게.