오늘은 다익스트라 알고리즘에 대해 간단하게 알아보고, 문제에는 어떻게 적용이 되는지 !! 풀이까지 해보겠습니다. 재밌게 봐주세요 ⭐️
다익스트라 알고리즘 이란 ?
컴퓨터 과학에서, 데이크스트라 알고리즘(영어: Dijkstra algorithm) 또는 다익스트라 알고리즘은 도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘이다. 이 알고리즘은 컴퓨터 과학자 에츠허르 데이크스트라가 1956년에 고안했으며 삼 년 뒤에 발표했다.
출처 : 위키백과
간단하게 설명하자면 !?
다이나믹 프로그래밍을 활용한 대표적인 최단 경로(Shortest Path) 탐색 알고리즘입니다. 그래프 내의 특정 정점에서 갈 수 있는 다른 모든 정점까지의 최단거리를 알려줍니다. 하지만 이 때, 음의 간선을 포함할 수 없습니다.(주의 할 점 !!) 현실 세계에서는 음의 간선이 존재하지 않기 때문에, 다익스트라는 현실 세계에 사용하기 매우 적합한 알고리즘이라고 할 수 있습니다.
자세한 내용은 아래의 영상을 참고해주세요 🖥

다익스트라 알고리즘 (개념편)
https://www.youtube.com/watch?v=qaiuC3Q73-M
구체적인 작동 과정은 다음과 같습니다.
- 출발 노드를 설정한다.
- 출발 노드를 기준으로 각 노드의 최소 비용을 저장한다.
- 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택한다.
- 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신한다.
- 위 과정에서 3번-4번을 반복한다.
개념은 어느정도 이해가 됐다는 가정하에, 문제에 적용을 시켜보겠습니다 🤪
Leetcode 743. Network Delay Time
You are given a network of n nodes, labeled from 1 to n.
You are also given times, a list of travel times as
directed edges times[i] = (ui, vi, wi), where ui is the
source node, vi is the target node, and wi is the time
it takes for a signal to travel from source to target.
We will send a signal from a given node k.
Return the time it takes for all the n nodes
to receive the signal. If it is impossible for all
the n nodes to receive the signal, return -1.
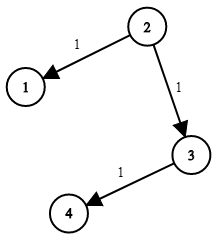
Example 1:
Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
Output: 2
Example 2:
Input: times = [[1,2,1]], n = 2, k = 1
Output: 1처음 접해보는 최단 거리 ( 다익스트라 ) 문제였다. 너무 어려웠다.
답지를 보고 코드를 하나하나 뜯어보자 !!
봐도봐도 모르겠으면 그냥 외워버린다는 마인드
정답코드
# class Solution:
# def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
"""
k부터 출발해 모든 노드가 신호를 받을 수 있는 시간을 계산하라.
불가능할 경우 -1을 리턴한다.
입력값 (u,v,w) 는 각각 출발지, 도착지, 소요 시간으로 구성되며,
전체 노드의 개수는 N으로 입력받는다.
"""
import collections
import heapq
times = [[2,1,1],[2,3,1],[3,4,1]]
# 주어진 입력 예시
n = 4
# 노드 개수
k = 2
# 출발점
# output = 2
graph = collections.defaultdict(list)
# 그래프 인접 리스트 구성
for u,v,w in times:
graph[u].append((v,w))
# 큐 변수 : [(소요시간, 정점)]
Q = [(0, k)]
# k 노드까지 가는데 걸리는 시간 (비용)
dist = collections.defaultdict(int)
# 우선순위 큐 최솟값 기준으로 정점까지 최단 경로 삽입
while Q:
time, node = heapq.heappop(Q)
# time(걸리는 시간), node(어디까지?)
# heappop 으로 최솟값을 빼오기 때문에 더 둘러서 오는(비용이 더 큰) 것은 포함 안함
if node not in dist:
dist[node] = time
for v,w in graph[node]:
# node에서 출발해서
# v노드까지 가는데 w만큼 소요
alt = time + w
# node 까지 오는데 걸린 시간 time + v 노드까지 가는데 걸리는 시간
# alt = v node 까지의 총 길이
heapq.heappush(Q, (alt,v))
# 모든 노드의 최단 경로 존재 여부 판별
if len(dist) == n:
# 모든 노드를 돌았나 판단
return max(dist.values())
# 그게 아니라면 뭐가 하나 빠졌다는 소리, 그럼 return -1
return -1