Big O notation(빅오 표기법)
빅오 표기법의 기초
빅오 표기법은 알고리즘의 최악의 경우 복잡도를 측정하는 기법이다.
보통 O(n)과 같이 표기하며 여기서 n은 입력의 개수를 의미한다.
따라서 n이 무한으로 접근할 때 무슨일이 일어날까? 정도로 생각하면 될 것 같다.
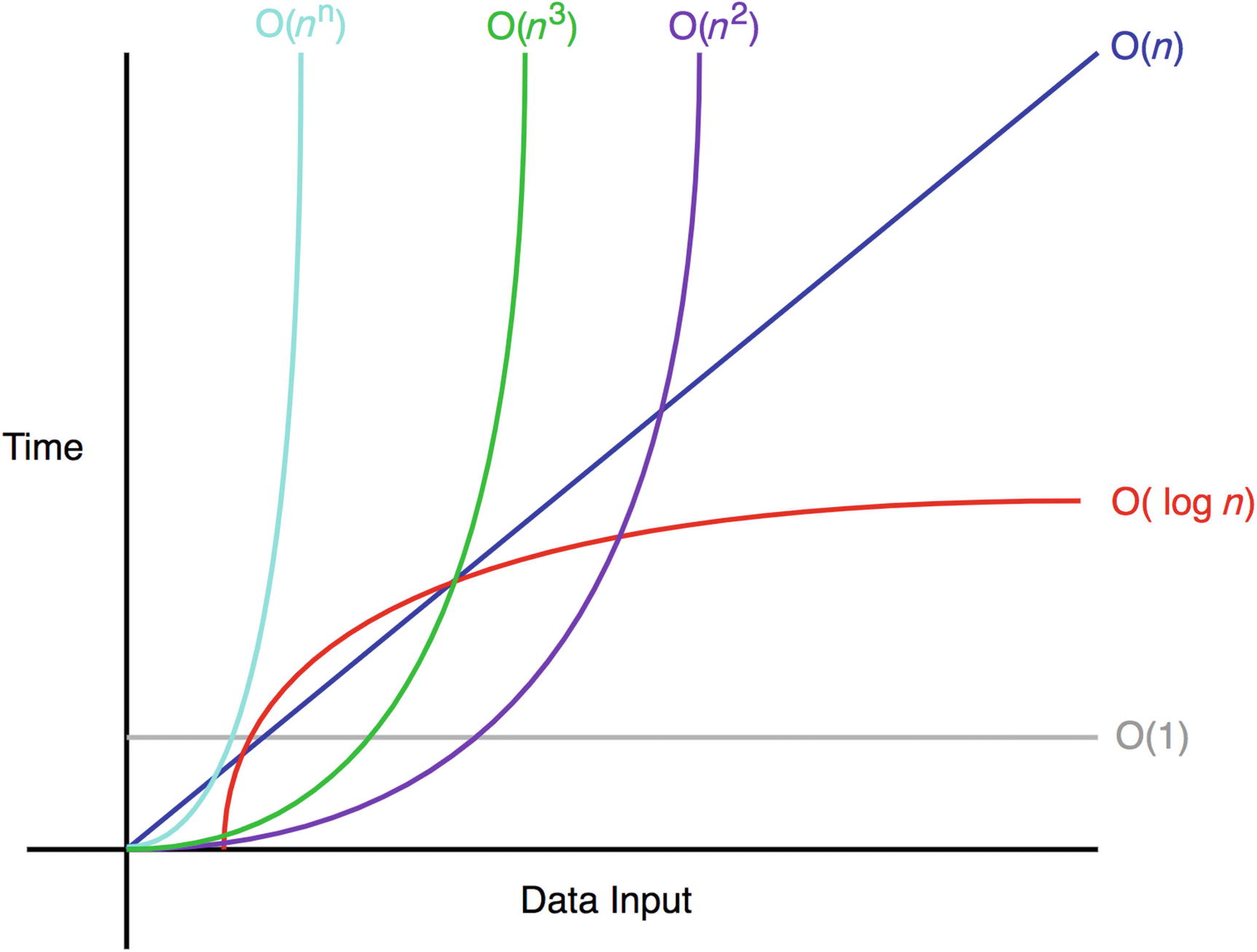
일반적인 빅오 복잡도의 모습이다.
고등학교 수학에서 흔히 볼법한 그래프이며, O(n) = n을 기준으로 지수함수(Exponential function)와 로그함수(Logarithm)가 대칭을 이루고 있음을 알 수 있다.
O(n)은 선형시간이고 최악의 경우에 n번의 연산을 수행해야 하는 알고리즘에 적용되므로
function exampleLinear(n) {
for(var i = 0; i < n; i++) {
console.log(i);
}
}위와 같은 코드가 가장 대표적인 예라고 할 수 있다.
console.log로 0부터 n-1까지 출력하는 코드이므로 n번 수행이 된다.
마찬가지로 O(n2)은 2차 시간이고, O(n3)은 3차 시간을 갖는다.
따라서 O(n2)은
function exampleQuadratic(n) {
for(var i = 0; i < n; i++) {
console.log(i);
for(var j = i, j < n; j++) {
console.log(j);
}
}
}위와 같은 코드로 나타낼 수 있다.
console.log로 0부터 n-1까지 출력하는 코드이므로 n번 수행되는 코드 안에 다시 한번 같은 반복문이 있으므로
n * n
마찬가지로 O(n3)은
function exampleCubic(n) {
for(var i = 0; i < n; i++) {
console.log(i);
for(var j = i; j < n; j++) {
console.log(j);
for(var k = j; k < n; k++) {
console.log(k);
}
}
}
}위와 같은 코드로 나타낼 수 있을 것이다.
마지막으로 로그함수에 대한 복잡성은
funtion exampleLogarithmic(n) {
for(i = 2; i <= n; i = i * 2) {
console.log(i);
}
}위와 같은 코드로 나타낼 수 있겠으며, 위의 코드의 복잡성은 O(log2 n)이다.
예를 들어
n = 16이라면,i = 2, 4, 8, 164가지의 경우가console.log에 의해 출력되며,
log2 16 = 4이다.
빅오 표기법의 규칙
빅오 표기법의 그래프는 x축은 입력의 갯수, y축은 시간을 나타낸다.
이를 통해 필요한 공간(추가적인 메모리)를 나타낼 수 있는데 이러한 알고리즘의 분석의 목표는 알고리즘의 효율성을 이해하는데에 있다.
하지만 우리는 이를 계산하기에 많은 어려움을 가지고 있기에 빅오 표기법은 개발자들이 편하게 이를 계산하기 위해 몇가지 규칙을 제공하고 있다.
1. Coefficient Rule : Get Rid of Constants(계수 법칙 : 상수를 제거하자)
상수 k가 0보다 클 때(k > 0), f(n) = O(g(n))이면 kf(n) = O(g(n))이다.
이는 입력의 크기 n이 무한에 가까워 지는 경우 양수인 k의 크기는 의미가 없기 때문이다.
양의 무한대에 그 어떤 양수를 곱하더라도 결과 값은 결국 양의 무한대이다.
function a(n) {
var count = 0;
for(var i = 0; i < n; i++) {
count += 1;
}
return count;
}시간복잡도가 O(n)인 코드이다.
function a(n) {
var count = 0;
for(var i = 0; i < 5 * n; i++) {
count += 1;
}
return count;
}여기서 n에 5를 곱해주면 시간복잡도는 5 * O(n)인 코드가 된다.
하지만 계수 법칙에 의해 5는 무시되며 시간복잡도는 O(n)이 된다.
2. Sum Rule : Add Big-Os Up(합의 법칙 : 빅오를 더하자)
f(n) = O(h(n))이고, g(n) = O(p(n))이면 f(n) + g(n) = O(h(n) + p(n))이다.
이해하기 어렵다면 간단한 예를 봐보도록 하자.
function a(n) {
var count = 0;
for(var i = 0; i < n; i++) {
count += 1;
}
for(var i = 0; i < 5 * n; i++) {
count += 1;
}
return count;
}계수 법칙에서의 시간복잡도 O(n)과 5 * O(n)을 하나의 함수안으로 넣었다.
첫번째 for문에 의해 n번 반복하고, 두번째 for문에 의해 5n번 반복한다.
이를 return하므로 6n의 값을 얻을 수 있다.
하지만 계수 법칙에 의해 시간 복잡도는 최종적으로 n이 된다.
3. Product Rule : Multiply Big-Os(곱의 법칙 : 빅오를 곱하자)
f(n) = O(h(n))이고, g(n) = O(p(n))이면 f(n) * g(n) = O(h(n) * p(n))이다.
예를 보고 이해해 보도록 하자.
function a(n) {
var count = 0;
for(var i = 0; i < n; i++) {
count += 1;
for(var i = 0; i < 5 * n; i++) {
count += 1;
}
return count;
}합의 법칙에서의 코드를 가져왔다. 다른 점이 있다면 첫번째 for문안에 두번째 for문이 들어가 있다는 점이다.
이를 통해 우리는 직관적으로 n * 5n의 시간 복잡도를 갖는다는 것을 알 수 있다.
그렇다면 위의 코드의 시간 복잡도는 5n2일까? 여기에서도 계수 법칙은 적용되어 최종적인 시간 복잡도는 n2이 된다.
4. Polynomial Rule : Big-O to the Power of k(다항 법칙 : 빅오의 k승)
f(n)이 k차 다항식이면 f(n) = O(nk)이다.
이 또한 예를 보면
function a(n) {
var count = 0;
for(var i = 0; i < n * n; i++) {
count += 1;
}
return count;
}위의 예에서 f(n) = n2이 되면서 시간 복잡도는 O(n2) 이 된다.
n * n대신 n * n * n이라면 시간 복잡도는 O(n3)이 될 것이다.
Summary
Big O notation은 알고리즘의 효율을 분석하고 비교하는데 중요하다.
여기에는 크게 4가지의 법칙이 있는데, 다항 법칙, 곱의 법칙, 합의 법칙을 시행 한 후 마지막에 계수 법칙을 적용한다.
Reference
