[논문 리뷰] Item-based collaborative filtering recommendation algorithms

정준환·2022년 10월 2일

논문리뷰 추천시스템

논문리뷰

목록 보기

1/5

논문의 내용을 이해를 위해 제 마음대로 재구성 하였으며 틀린 내용이 있을 수 있습니다. 발견 시 댓글로 알려주시면 감사하겠습니다.

1줄 요약

Item-based collaborative filtering 이 User-based collaborative filtering 보다 더 좋다.

1. Introduction

우리가 노래를 추천 받는 상황을 가정해보자. 추천을 받는 방법은 세가지 정도가 쉽게 떠오른다.

그냥 실시간 Top 100 듣기
나랑 취향이 비슷한 사람들이 듣는 노래를 듣기
내가 좋아하는 노래랑 비슷한 노래 듣기

첫번째 경우 나에게 맞는 추천보다는 조금 더 보편적인 추천이 될 확률이 크다. 따라서 모든 유저들에게 빠르게 추천은 가능하겠지만, 정확한 추천은 아래 두가지 경우에 비해 많이 떨어질 것이다. 이 상황이 노래가 아니라 쿠팡에서 상품을 주문한다고 생각하면 왜 정확하지 않은 추천이 될 것인지 쉽게 받아들일 수 있다.

두번째 추천 방법을 User-based collaborative filtering(CF), 세번째 방법을 Item-based CF라고 부른다.

이 논문은 2001년에 나온 논문인데, 이 시기에는 user-based CF가 대세였나보다. 멜론같은 사이트를 들어가서 노래를 추천 받는다고 하면 user-based CF를 이용해서 노래를 추천해줬다고 한다. (진짜 멜론이 썼는지는 모른다) 실제로 추천 자체에는 큰 문제 없이 잘 써먹고 있었는데 시간이 지나면서 인터넷 사용이 더 많아지고, 데이터의 양이 많아지면서 두가지 Challenge가 부각되었다.

Scalbility
(그 때 당시를 기준으로) user-based CF는 수만개의 유저 데이터를 실시간으로 처리할 수 있는데, user와 item이 모두 늘어버리면서 요새 수요는 수천만개의 데이터를 실시간으로 처리를 해야한다. 당연히 느려질 수 밖에 없다. 쿠팡 들어갔는데 상품 추천한다고 느려지면 스트레스 잔뜩 받겠지? 실제로 요새는 이런 정확한 추천도 추천인데 얼마나 로딩이 빨리 되느냐도 엄청 중요한 문제라고 들었다.
Quality
당연히 더 정확한 추천에 대한 갈증이 있을 수 밖에 없다.

빠른 추천과 정확한 추천. 이 두개는 당연히 trade-off가 존재해서 기존의 user-based CF로는 이 두마리 토끼를 한번에 잡을 수 없다. 이때 기가 막힌 방법이 나타나는데, 바로 item-based CF다. 이게 일단 위에서 설명한 예시를 보면, user-based CF나 item-based CF나 뭐가 크게 다른가? 라는 생각이 드는게 당연하다. 차이점은 user와 item에서 나온다.

먼저 user-based CF를 보자. 나는 힙합을 좋아하는데, 그러면 멜론은 나한테 내가 아직 듣지 않은 노래들 중, 힙합을 좋아하는 다른 사람들이 듣는 노래를 추천해 줄 것이다. 이 과정을 정리해보면 아래와 같다.

나랑 비슷한 노래를 듣는 사람들을 찾는다.
그 사람들이 좋아하는 노래를 뽑아낸다. (점수를 매겨 정렬한다)
내가 아직 들은 적이 없다면, 나한테 추천해준다.

비슷하게 item-based CF는 아래와 같다.

데이터베이스에 존재하는 모든 노래들에 대해 비슷한 노래들을 미리 찾는다.
1에서 찾은 것을 바탕으로 내가 좋아할 법한 노래를 뽑는다. (마찬가지로 점수를 매겨서 정렬해준다)
2번에서 나온 리스트 중, 좋아할 만한 노래를 추천해준다.

결국 item-based CF든, user-based CF든 2나 3의 process는 비슷한데, 1번에서 미리 계산을 해 놓을 수 있는지의 대한 여부가 차이가 난다. 이는 user와 item의 특성에서 기인한다.

나는 지금 힙합을 좋아하지만, 당장 한 달 뒤에는 발라드를 듣고 있을 수 있다. 즉, 나와 비슷한 사람의 집단이 계속해서 바뀔 수 있다는 것이다. 하지만 item의 경우에는 한번 출시된 음악은, 비슷한 음악의 집단이 바뀔 가능성이 상대적으로 낮다. 따라서 user의 경우 비슷한 집단 (neighbors)를 미리 계산할 수 없지만, item의 경우 neighbors를 미리 계산 해놓을 수 있는 것이다. 따라서 추천이 빨라진다.

이를 논문에서는 item이 user보다 비교적으로 static 하다고 표현했다.

이제 앞으로의 내용은 크게 세가지 파트로 나누어 볼 수 있다. 글을 읽다가 흐름을 놓친 것 같다면 여기로 돌아와서 내가 어느 위치쯤에 있는지 생각해보면 이해에 도움이 될 것 같다.

item-based CF를 하는 방법

수식으로 정리

실제 Data로 계산해보기

2. Notation 정리

우리가 이 논문에서 하고자 하는 것은 item-based CF가 user-based CF보다 낫다는 것을 보여주는 것이다. 그것을 보여주기 위해 우리는 몇가지 용어 및 기호들을 정리하고 가도록 하자.

{\Large u} = \{u_1, u_2, \cdots, u_m\} \\ \mathcal{I} = \{i_1, i_2, \cdots, i_n\}

$m$ 명의 유저, $n$ 개의 아이템을 위처럼 표현한다. 각각의 유저 $u_i$ 는 어떤 아이템들을 선택했을텐데, 이를 $I_{u_i}$ 라고 표현한다. 그러면 유저는 explicit 이든 implicit이든 아무튼 이에 대한 평가가 내려져 있다.

당연히 $I_{u_i} \subseteq \mathcal{I}$ 이고, 공집합 일 수도 있다. active user 라고 부르는 $u_a$ 가 있는데, 이게 우리가 상품을 추천해주고 싶은 유저라고 하자. 이때 아이템은 아래 두가지 방법으로 찾는다.

Prediction

$P_{a, j}$ 라고 하는 숫자를 계산해보기. 어떤 아이템 $i_j \notin I{u_a}$ (즉, active user가 아직 안고른 아이템) 에 대해서 유저가 얼마나 좋아할 것 같나요? 에 대한 대답이다. $u_a$ 가 지금껏 해온거랑 같은 스케일로 예측해야 한다. 5점 만점이면 5점 만점, 좋음 안좋음 0 1 이면 0과 1 이런식으로.

Recommendation

$I_r$ 이거는 N개의 아이템 리스트다. 당연히 $I_r \sub \mathcal{I}$ 이고, active user가 제일 좋아할 것 같은 아이템들로 꾸린 집합이다. 당연히 얘네는 active user가 아직 구매하지 않은 것들로만 구성되어 있어야 한다. 즉, $I_r \cap I_{u_a} = \empty$

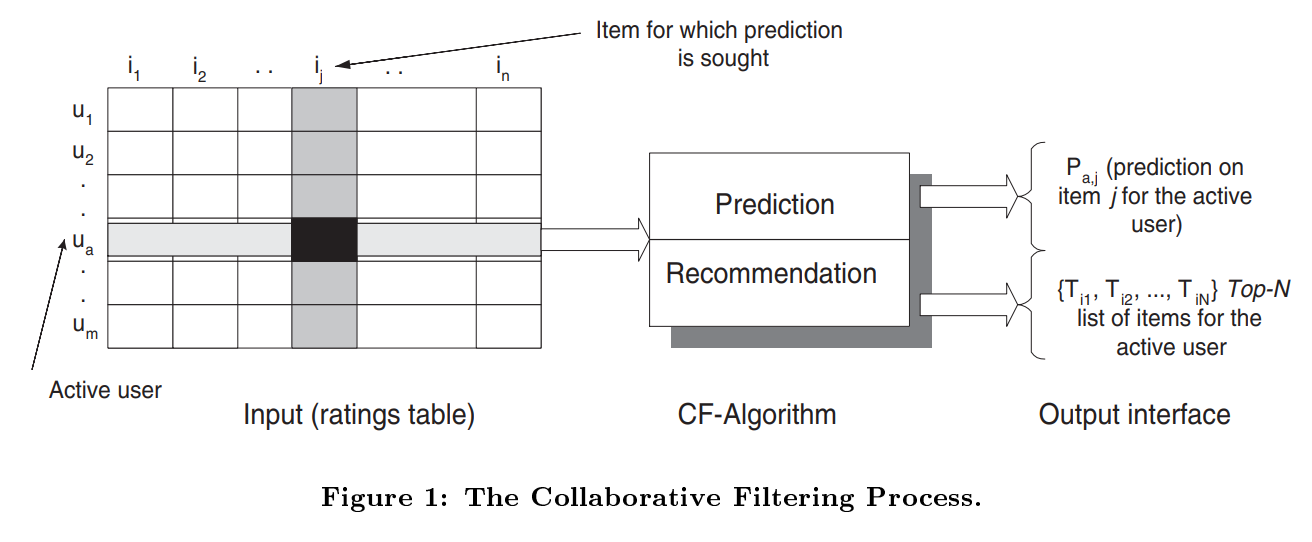
이 Figure 1은 CF가 뭔지 보여준다. $m$ X $n$ user-item matrix를 $\mathcal{A}$ 라 하자. $a_{i,j}$ 는 유저가 매긴 점수를 의미하고, 모든 유저가 모든 아이템을 사본건 아니니까 대부분 0임을 알 수 있다. 즉, $\mathcal{A}$ 는 sparse하다.

이제 이 matrix를 item-based CF를 통해 분석해, 좋은 아이템을 추천해보자.

3. Item-based CF Algorithm

위 2. Notation 정리 내용은 item-based CF를 사용하지 않아도 기본적인 user-item matrix $\mathcal{A}$ 를 분석하기 위한 내용이다. 이제 item-based CF에 초점을 맞춰보자.

우리가 하고자 하는 것은 active user $u_a$ 가 target item $i$ 에 대해서 몇점의 점수를 매길지 계산하면 된다. $i$ 에 대한 점수를 매길 수 있다면, 모든 아이템들에 대해서 점수를 매겨보고, 가장 높은 점수를 갖는 아이템을 추천하면 된다.

이제 우리는 $\mathcal{A}$ 를 통해서 target item $i$ 와 다른 아이템들 사이의 유사도를 측정한다. 그중에 active user $u_a$ 가 구매 한 것 중, $k$ 개의 높은 유사도를 갖는 아이템을 뽑았다고 하면 neighbors라고 하는 $\{i_1, i_2, \cdots , i_k \}$ 이라고 나타낼 수 있고, 이때 각각의 아이템들에 대한 유사도를 $\{s_{i1}, s_{i2}, \cdots, s_{ik}\}$ 라고 하자.

위의 두 집합을 찾으면, 유사도와 $u_a$ 가 해당 아이템들에게 매긴 점수를 이용하여 예측치를 쉽게 구해낼 수 있다.

이제 우리가 해야 할 일은 두가지다.

아이템 간 유사도를 계산해 비슷한 아이템 집합을 뽑아내기
계산된 유사도를 통해 예측치 계산하기

3.1 Item Similarity Computation

먼저 아이템 간 유사도를 계산해보도록 하자. 아이템 $i, j$ 가 있다고 치면 이 둘의 유사도 $s_{i, j}$ 를 계산하는 기본적인 아이디어는 다음과 같다.

일단 $i$ 와 $j$ 를 모두 구입한 사람만 쳐다본다. 둘 다 사본 user들 만 둘의 유사도에 영향을 미칠 수 있다.

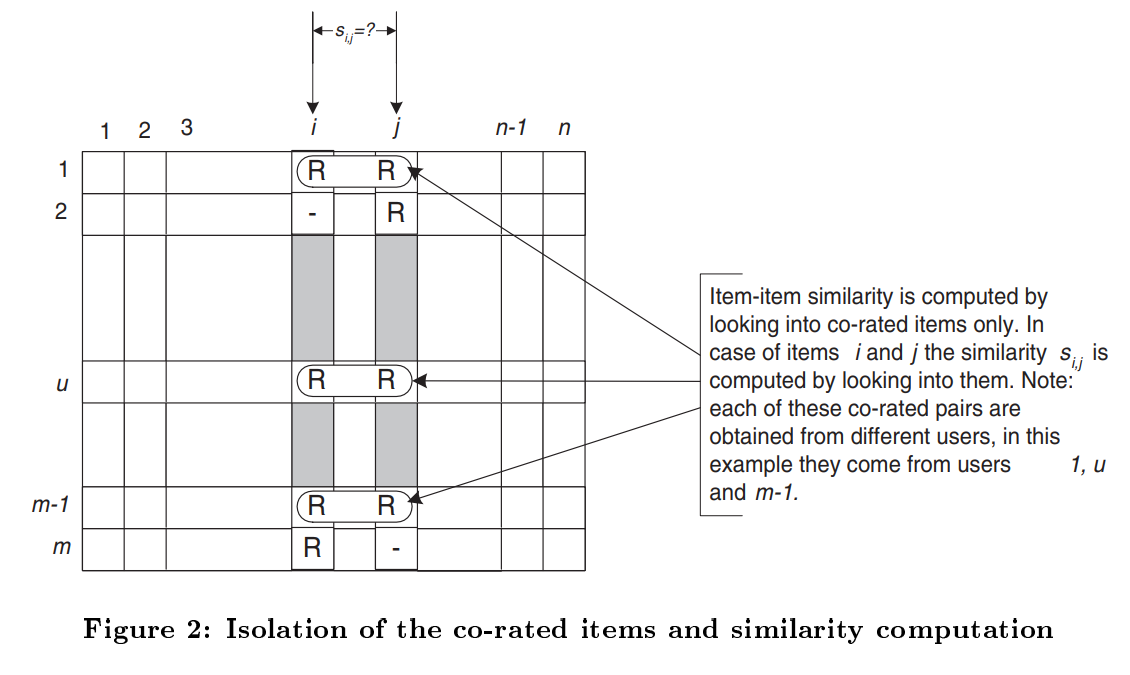
위의 Figure 2는 아이템 간 유사도를 잘 설명하는 그림인데, row 는 유저, column 은 아이템이다. 위 그림을 보면 아이템 $i$ 와 $j$ 를 둘 다 구매한 유저인 1, $u$ , $m-1$ 만 딱 찝어서 보는 것을 확인할 수 있다.

이제 이렇게 $i$ 와 $j$ 만을 구매한 유저만을 골라내는 작업을 isolation이라고 하는데 이게 끝나면 유사도를 측정하는 방법은 대표적으로 아래와 같다.

Cosine-based Similarity
Correlation-based Similarity
Adjusted Cosine Similarity

침착하게 하나씩 확인해보자.

3.1.1 Cosine-based Similarity

$\cos$ 함수를 이용해서 유사도를 측정하는 방법이다. 위 Figure 2에서 아이템 $i$ , $j$ 에 해당하는 열을 각각 벡터로 보고 두 벡터 사이의 각도를 유사도라고 생각하면 된다.

sim(i,j)=\cos(\vec i, \vec j) = \frac{\vec i \cdot \vec j}{\|\vec i\| * \|\vec j\|}

rating 되지 않은 항목은 0점이라고 하면, 이 과정에서는 결과적으로 한쪽이 0이라면 값이 무시되므로 굳이 isolation의 과정을 거치지 않아도 무방함을 확인할 수 있다.

3.1.2 Correlation-based Similarity

다음으로는 피어슨 상관계수 $corr_{i, j}$ 를 이용하는 방법이다. 앞선 cosine-based 방법과는 다르게, 뒤에 나오는 adjusted cosine 방법도 마찬가지로 isolation이 반드시 선행 되어야한다.

$U$ : 두 아이템 모두 구매한 유저들의 집합 (isolation)
$R_{u,i}$ : 유저 $u$ 가 아이템 $i$ 에 대해서 평가한 점수
$\bar R_i$ : 아이템 $i$ 의 평균 점수

라고 한다면 유사도는 아래와 같이 계산할 수 있다.

sim(i, j) = \frac{\sum_{u \in U} (R_{u, i} - \bar R_i)(R_{u, j} - \bar R_j)} {\sqrt{ \sum_{u \in U} (R_{u, i} - \bar R_i)^2} \sqrt{ \sum_{u \in U} (R_{u, i} - \bar R_i)^2} }

3.1.3 Adjusted Cosine Similarity

앞의 두가지 방법은 user들의 성향을 고려하지 않았다. 예를들면 영화 평론가 박평식님은 점수를 짜게 주시기로 굉장히 유명하다. 그에 반해 나는 적당히 재밌게 봤던 영화에 10점을 주었다고 생각해보자. 그 분의 10점과 내 10점은 가치가 다르게 매겨져야 하는것이 옳다. 평론가여서가 아니라, 원래 짜게 주시기 때문이다. 이러한 문제 때문에, user들의 평균 점수를 고려해준 방법이 adjusted cosine similarity 방법이다.

$\bar R_u$ 를 한 유저 $u$ 의 평균 점수라고 하면 아래와 같이 나타낼 수 있다.

sim(i, j) = \frac{\sum_{u \in U} (R_{u, i} - \bar R_u)(R_{u, j} - \bar R_u)} {\sqrt{ \sum_{u \in U} (R_{u, i} - \bar R_u)^2} \sqrt{ \sum_{u \in U} (R_{u, i} - \bar R_u)^2} }

위 세가지 방법을 이용하면 아이템 $i$ , $j$ 간의 유사도 $s_{i, j}$ 를 측정 할 수 있고, 이를 싹 정렬해서 특정 아이템 $i$ 와 가장 유사한 $k$ 개의 아이템 집합 $\{i_1, i_2, \cdots , i_k \}$ 과 그때의 유사도 $\{s_{i1}, s_{i2}, \cdots, s_{ik}\}$ 를 얻어낼 수 있다. 이 집합은 active user $u_a$ 가 구매하지 않은 아이템은 포함하지 않아야 한다.

3.2 Prediction Computation

어떤 방법을 사용하던 간에, 우리는 아무튼 아이템 집합 $\{i_1, i_2, \cdots , i_k \}$ 을 얻어 낸 상태다. 이제 이 집합을 이용해서 user $u$ 가 item $i$ 에 대해 매길것으로 예상되는 점수 $P_{u, i}$ 를 계산할 수 있다.

여기에도 similarity computation 과 마찬가지로 다양한 방법들이 쓰일 순 있겠지만, 나는 Weighted Sum 을 이용한 방법만 정리해보겠다. 식으로 써보면 아래와 같다.

P_{u,i} = \frac{\sum_{\text{all similar items, N}} (s_{i,N} * R_{u, N})}{\sum_{\text{all similar items, N}} (|s_{i, N}|)}

쉽게 생각하면 $i$ 와 유사한 아이템들에 대해서 유사도와 점수를 곱해준 값에 유사도의 합을 나눠 준 것이다.

Weighted Sum 말고 regression 을 이용한 방법도 논문에서 간략히 소개하지만, 넘어가겠다.

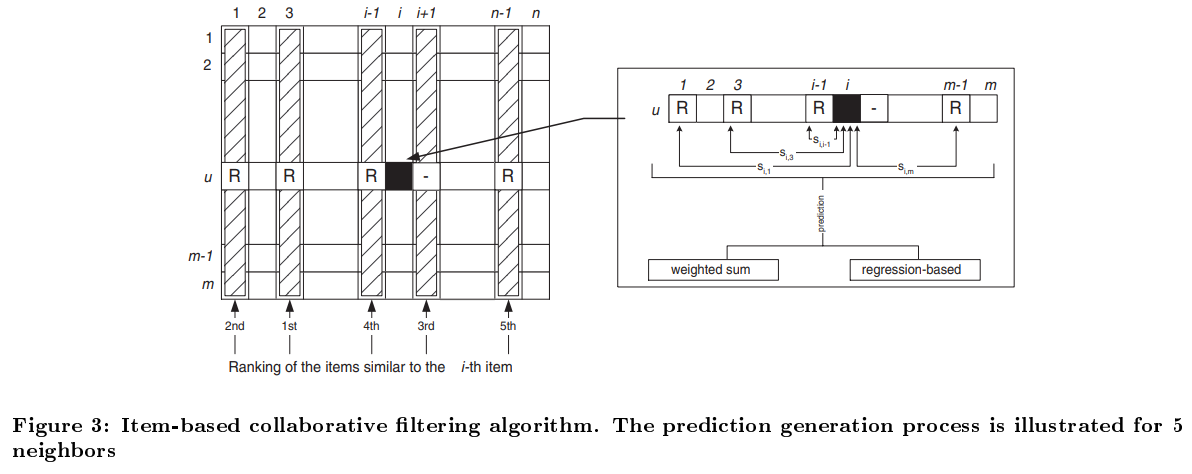
위의 Figure 3을 보면 설명되어있듯이, 유사도 계산을 통해 가져온 5개의 아이템들을 통해서 검정색으로 색칠된 칸의 값을 예측한다.

이제 우리는 어떤 active user $u_a$ 가 아직 구매하지 않은 item들에 대해서 몇점을 매길지 모두 계산할 수 있다. 그렇다면 이중 가장 높은 점수를 갖는 N개의 아이템을 추천해준다면 끝이다!

3.3 Performance Implications

이런 방법이 기본적인 item-based CF의 큰 흐름이다. 위에서 언급한 것 처럼 item간 similarity는 미리 계산이 가능하고, 저장해놓았다가 꺼내서 쓰면 시간적으로 큰 절약이 가능하다. 가장 쉬운 방법은 $n$ 개의 아이템들에 대해서 similarity를 모두 다 계산해놓고 다 저장해놓으면 된다. 그러면 우리는 $O(n^2)$ 만큼의 공간이 필요한데, $n$ 이 무지막지하게 큰 현 시장에는 좀 부담스럽다.

여기서 기가막힌 아이디어가 하나 나오는데, 우리는 3. Item-based CF Algorithm 에서 $k$ 개의 most similar item만을 필요로 한다고 언급했다. 그렇다면 굳이 모든 아이템들의 similarity를 저장해서 $O(n^2)$ 만큼의 공간을 사용하는것이 아니라, 필요한 만큼만 저장하면 되지 않을까? 일반적인 상황에서 $k << n$ 이니까 공간을 많이 절약할 수 있을 것이다.

이 상황에서 이 필요한 만큼 자르는 것을 model size $l$ 이라고 한다. 그러면 우리는 space complexity를 $O(nl)$ 로 줄일 수 있다. 물론 원래 $n$ 개의 데이터를 가지고 평가 하던것을 $l$ 개로 잘라서 보니까 quality-performance trade-off가 존재할 수 밖에 없다. 근데 위에서 제시한것 처럼 어차피 우리는 $n$ 개 중 $k$ 개만 쓰면 되니까 적당히 잘라내자는 아이디어를 제시한 것이다. 따라서 quality 면에서 큰 차이가 없을 것이라고 예측해볼 수 있고, 실제 실험 결과, 큰 차이가 없음을 확인할 수 있다.

어차피 $n$ 개 중에 $k$ 개의 데이터만 뽑아서 보는데 뭐하러 다 저장을 하냐! 적당히 잘라서 저장하는게 더 효율적이다 라는 관점이다.

4. Experimental Evaluation

이제 앞선 주장이 맞는지 확인해보는 시간이다. 결과는 두가지 종류로 나눠볼 수 있다.

Quality : 얼마나 정확한 추천을 했느냐
Performance : 얼마나 빨리 추천을 했느냐

진행하기에 앞서, 실험에 대한 기본 정보는 다음과 같다.

MovieLens에서 10만개의 평가 데이터를 얻었고 $943$ X $1682$ 의 user-item matrix $\mathcal{A}$ 를 얻었다. 이 데이터들을 training set이랑 test set으로 분리해서 사용했고, 그 비율을 $x$ 라고 하자.

4.1 Experimental Procedure

실험 과정은 아래와 같다.

Experimental steps
- training, test set 분리
- hyper parameter 최적화
Benchmark user-based system
- 비교를 위해 user-based CF에 대해서 마찬가지 시도

4.2 Quality Experiments

먼저 얼마나 정확한 추천을 했는지 알아보도록 한다. 이 논문에서는 Mean Absolute Error (MAE) 방법을 사용했다. 식은 아래와 같다.

MAE = \frac{\sum_{i=1}^N |p_i-q_i|}{N}

단순히 내 예측 값과 참값의 차이를 절댓값 씌워 평균을 취한 값이다. 당연히 이 MAE가 작을수록 잘 예측한 것이다. 물론 이것 말고도 RMSE나 Correlation 등 다른 방법을 써도 된다.

4.2.1 Hyperparameter Tuning

평가를 하기 전 진짜 마지막 단계다. 하이퍼 파라미터 튜닝을 진행한다. 앞서 3.1 Item Similarity Computation 에서 소개한 세가지 방법중 무엇을 선택할지, Training/Test ratio $x$ 는 몇으로 할지, neighborhood size $k$ 는 몇으로 할지 선정해야 한다.

Training set을 다시 training, validation으로 분할해서 튜닝을 진행했고, 결과는 아래 그림들과 같다.

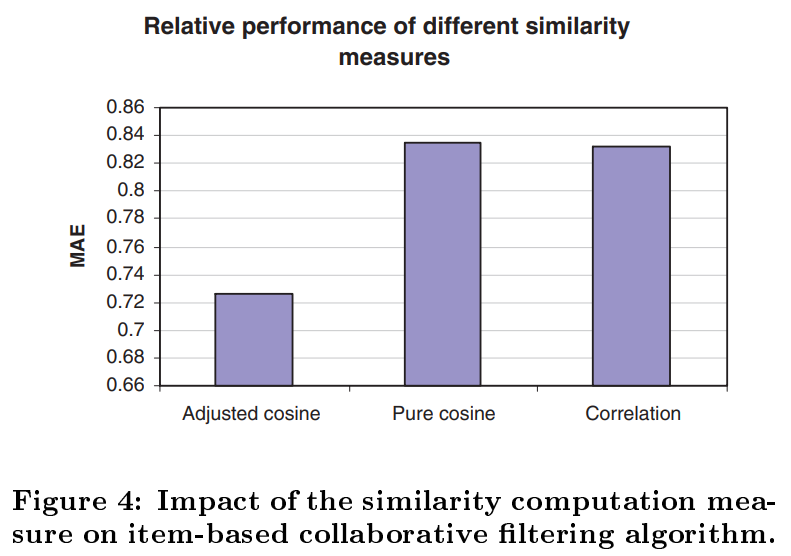
Figure 4에서 보는것처럼 Adjusted cosine 이 다른 방법보다 좋아서 similarity 계산에는 이것을 사용했다.

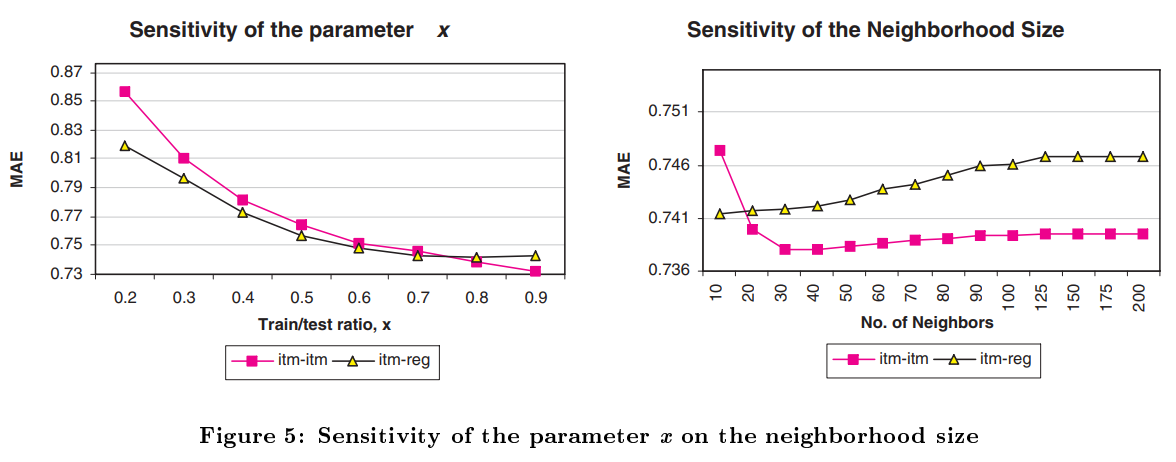
Figure 5는 흐름상 넘긴 regression 도 이용하여 $x$ 와 Neighborhood size $k$ 를 측정한다. 각각 0.8과 30을 선정했다.

4.2.2 Result - Quality

드디어 모든것이 끝났다. 이제 Item-based CF와 User-based CF를 비교만 하면 된다. 논문에서는 Item-based CF도 마찬가지 방법으로 최적의 하이퍼 파라미터 튜닝을 마쳤다고 한다.

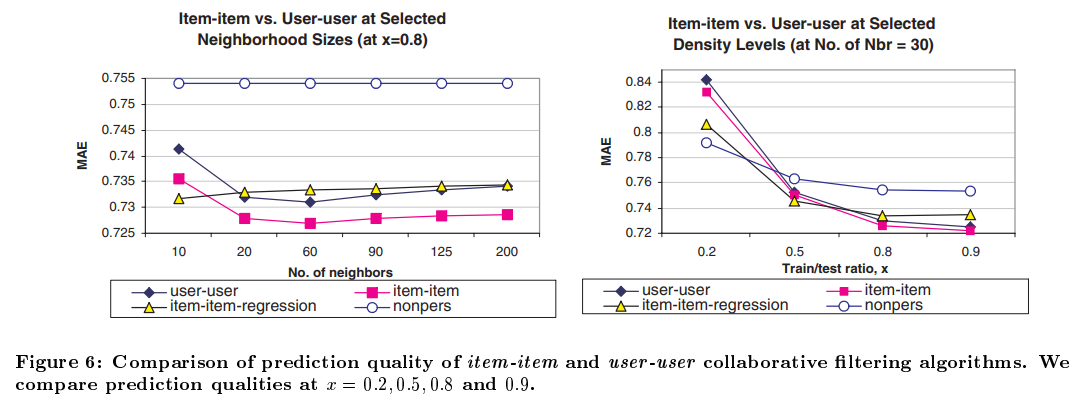
Figure 6은 논문의 결과를 보여준다. item-item-regression이나 nonpers는 과감하게 무시하고 user-user와 item-item만 보도록 하자.

왼쪽 그림은 Neighborhood size를 바꿔가면서 측정한 결과, 오른쪽 그림은 $x$ 를 바꿔가며 측정한 결과인데 어떠한 경우에서도 Item-based CF가 user-based CF보다 더 높은 성능을 보임을 확인할 수 있다.

결론적으로, Item-based CF가 더 빠르고 정확하다.

4.3 Sensitivity of the Model Size

앞서 3.3 Performance Implications 에서 언급한 내용을 직접 테스트 해보자. $n$ 개의 아이템에 대해서 $n$ 개의 similarity를 모두 저장하는것이 아닌, model size $l$ 만큼만 저장한다. 그 후에, $k$ 개의 neighbors에 따라서 3.2 Prediction Computation 의 방법대로 진행하면 된다. 이 때, $k$ 의 값은 model size $l$ 에 따라 당연히 달라진다. 이 실험에서는 각각의 모델 사이즈에 대해 또 다시 하이퍼 파라미터 튜닝을 진행해 적절한 값을 찾아주었다.

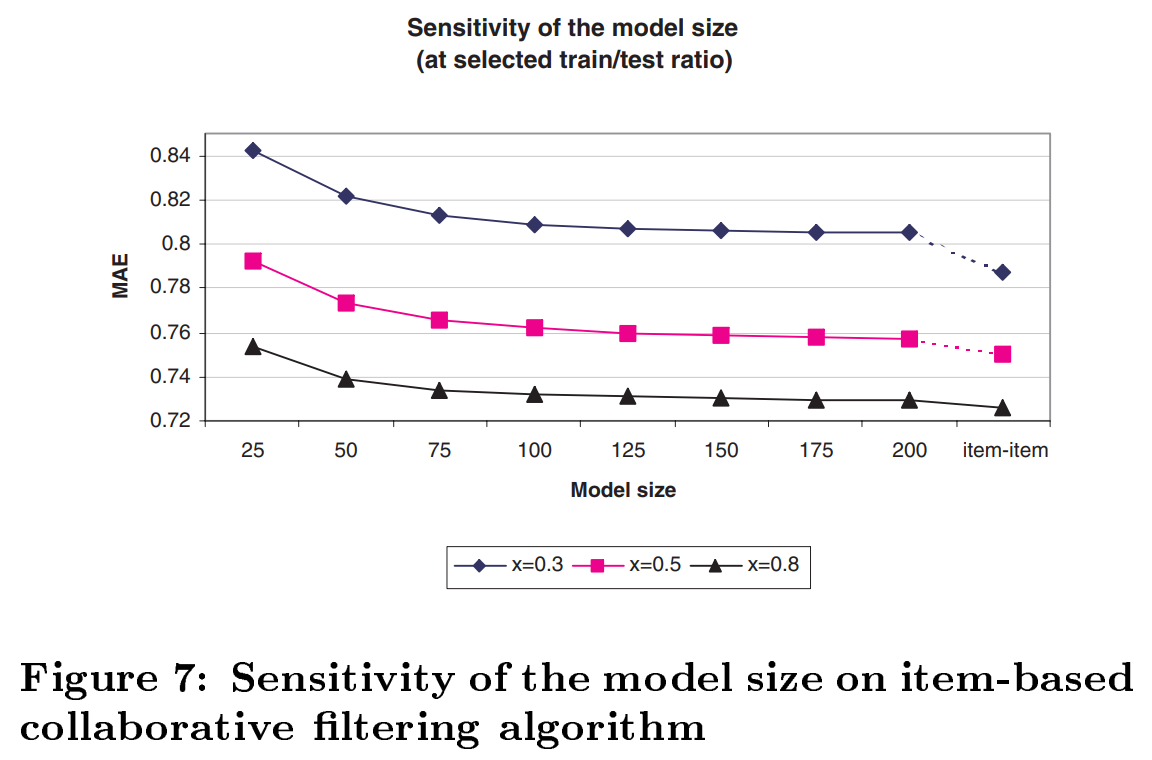
위의 Figure 7은 각각의 model size에 따른 MAE다. 제일 마지막 item-item 항목은 이미 위에서 진행한 n개의 아이템을 모두 사용한 기본적인 Item-based CF를 의미한다.

$x = 0.8$ 일 때를 기준으로 값을 살펴보면
$l=25$ 일 때, MAE = $0.754$
$l=50$ 일 때, MAE = $0.738$ 이다.
item-item의 경우는 $l = n$ 인 경우 이므로,
$l = 1682 \cdot 0.8 = 1345$ 일 때, MAE = $0.726$ 이다.

즉, 우리는 1.9%의 아이템만을 활용해서 96%의 효과를,
3%의 아이템만을 활용해서 98.3%의 효과를 낼 수 있는 것이다.

위 3.3 Performance Implications 에서 예측한 내용을 실험적으로 증명했다.

모든 아이템들에 대해 Similarity를 다 저장할 필요 없이 적절한 모델 사이즈 $l$ << $n$ 을 정해서 잘라내면 훨씬 효율적이다.

4.3.1 Impact of the model size on run-time and throughput

바로 앞에서 $O(n^2)$ 으로 저장 할 필요 없이 $n$ 에 비해 충분히 작은 $l$ 에 대해서 $O(nl)$ 로 저장해도 예측 정확도에 큰 차이가 없음을 확인했다. 그렇다면 이제 이로 인해서 얼마나 더 빠른 예측을 할 수 있는지에 대해 확인해보도록 한다.

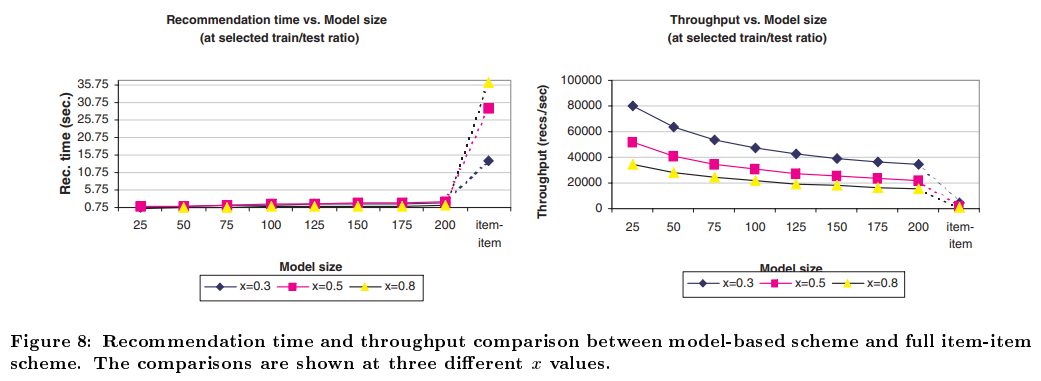
먼저 위 Figure 8의 왼쪽 그림은 model size $l$ 에 따라 추천에 걸리는 시간 그래프다. 즉 10만개의 데이터가 있으니까 $x=0.8$ 일 경우, 2만개의 추천을 몇 초 만에 완료하냐에 대한 그래프다. 그냥 뭘 비교 해 볼 필요도 없이 일단 무조건 작은게 좋은게 눈에 보인다.

여기서 약간 주의해야 할 점이, $x$ 에 따라 예측해야하는 데이터가 다르기 때문에 왼쪽 그래프는 사실 조금 부족하다. 우리가 궁금한건 결국 시간당 얼마만큼의 계산을 할 수 있느냐이기 때문이다. 그래서 왼쪽 그래프를 약간 변형해서 $y$ 축을 throughput (predictions generated per second) 로 바꾸어 그린 결과가 오른쪽 그래프다. 물론 모델 사이즈 $l$ 이 작을 때, 더 많은 추천을 할 수 있다는 사실은 변함 없다.

5. 결론

사실 Figure 6을 보면 Item-based CF나 User-based CF나 막 엄청난 차이를 보여주진 않는다. Item-based CF의 진가는 정확도가 아니라 속도에서 나타나는데, 왜냐하면 아이템은 상대적으로 static 하기 때문에 pre-computing이 가능하기 때문이다. 심지어 우리는 3.3 Performance Implications 이랑 4.3 Sensitivity of the Model Size 에서 model size를 확 줄이면 quality 측면에서는 거의 비슷하지만 속도는 확연히 빠른 결과를 확인할 수 있었다. 그러니까 이거 쓰자 이거 좋다!

정준환

다음 포스트