Taylor Series, 혹은 Taylor Expansion에 대해서 알아보자.

개념

---

개념을 간단하게 이해해보자.

어떤 함수 $f(x)$ 를 어떤 점 $x=a$ 부근에서 간단한 다항함수의 형태로 근사해보고자 한다. $f(x)$는 $\sin x, \cos x$ 과 같은 삼각함수 일 수도, $e^x$와 같은 지수함수 일 수도 있다. 오차가 조금 있더라도, 이런 복잡한 형태의 함수를 다항함수로 표현 할 수 있다면 계산에 있어서 큰 이득을 볼 수 있다. 그래프로 살펴보자.

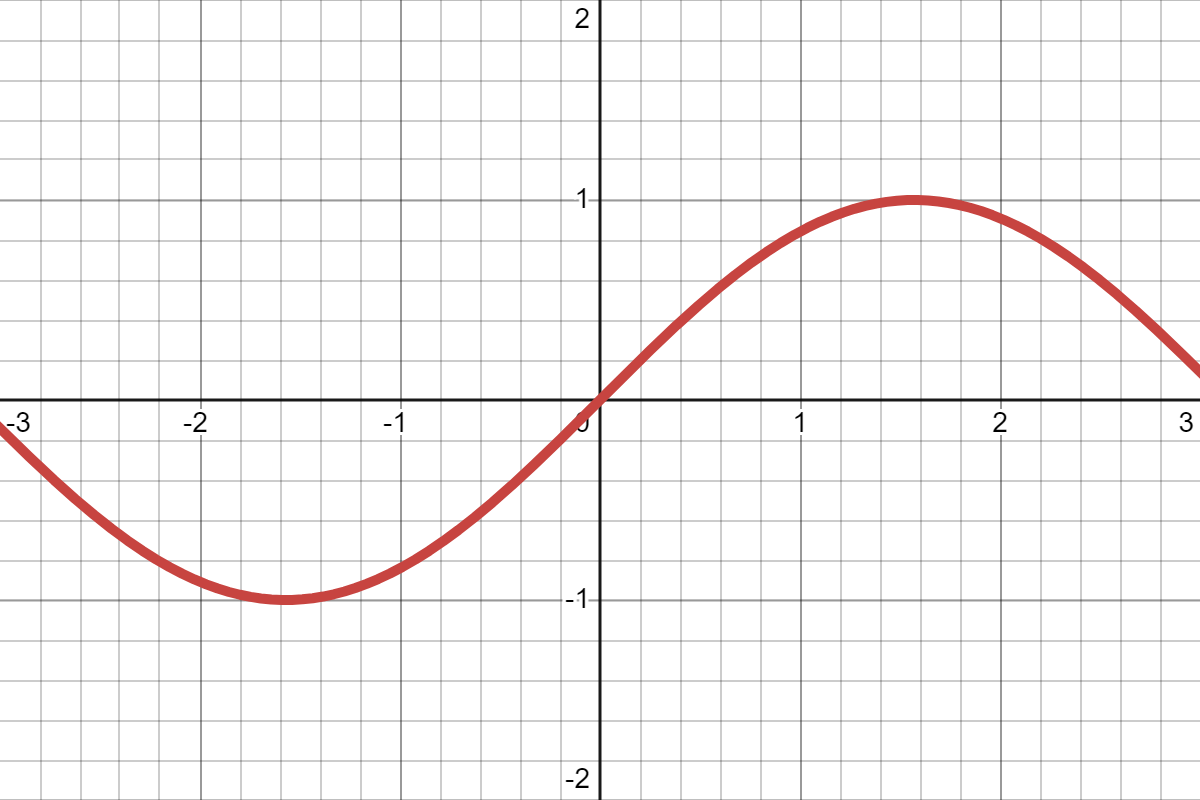
우리가 아는 일반적인 $\sin x$ 함수다. 적절한 다항함수들을 겹쳐서 그려보자.
파란색은 일차함수, 초록색은 삼차함수, 주황색은 오차함수다.

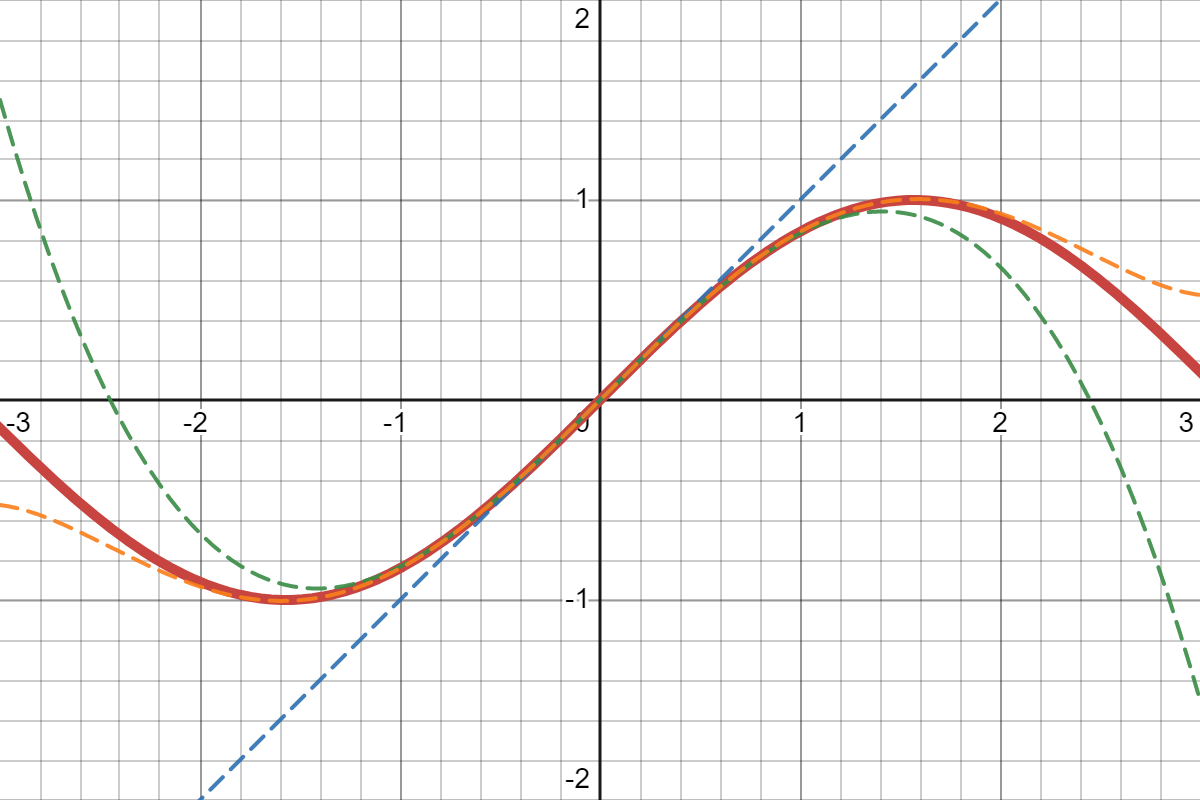
내 눈에는 차수가 높아질수록, $x=0$ 근처에서 충분히 $\sin x$를 잘 표현하고 있는 것 같다. 물론 $x=0$에서 멀어질수록, 정확성은 떨어진다. 위에서 말했듯, 목표는 $x=a$ 주변에서 잘 근사하는 것이기 때문에, 멀어졌을 때 다른 경향성을 띄는 것은 큰 문제는 아니다.

수식

---

수식은 언제나 어렵다. 모르겠으면 스크롤 쭉 내려서 식 9, 결론만 보자.

그럼 이제 $f(x)$를 잘 근사한 $n$차 함수 $g(x)$를 어떻게 찾을 수 있는지 알아보자. 나는 수학과는 아니라서, 수학적으로 엄밀하게 다가가지는 않겠다.

기본적으로 우리는 $n$차 함수를 아래와 같이 쓸 수 있다.

근데 $x=a$ 부근에서의 근사를 하는 것이니까, 조금 더 계산하기 쉬운 형태로 바꾸자.

어차피 $n$차식이라는 사실에 변함은 없다. (식 1과 식 2에서 $c_n$은 다른 수이다. 편의상 같은 기호를 사용했다)

이제 이 $g(x)$가 $f(x)$와 점 $x=a$ 부근에서 같다는 식만 세우면 끝이다. 너무 당연히

라는 식을 세워볼 수 있다. 그러면 식 2, 3에서 아래 식 4의 결과를 얻을 수 있다.

$f(a) = g(a)$ 만 성립할까? 함수 $x=a$ 근처에서 $f=g$ 이면 아래의 식 5가 모두 성립한다. 왜냐면 두 함수는 같으니까!
($f^{(n)}$은 $f$를 $n$번 미분한 식을 의미한다)

위 식 5를 계산하기 위해, $g(x)$를 미분 해보자. 식 2를 이용한다.

규칙이 대충 보인다. 어차피 $g(a)$를 구하고자 하는 것이니까, 뒤쪽에 $x-a$ 항이 남아있는 부분은 다 0이 된다. 한번 대입해보자.

이제 식 5, 6을 이용하면 적절한 $c_n$을 계산할 수 있다.

다 왔다. 이제 식 2와 식 7을 결합하면 우리가 원하던 함수 $g(x)$를 얻을 수 있다.

근데 사실 굳이 차수 $n$에 제한을 둘 필요는 없다. 따라서 일반적으로 아래와 같이 표현한다.

식 9에서 $a=0$인 특수한 경우를 매클로린 급수(Maclaurin Series) 라고 부른다.

이게 무슨 뜻이냐면, 함수 $f$가 $x=a$에서 $n$번 미분이 가능하면, $n$차함수로 근사할 수 있다는 뜻이다. $n$이 커지면 커질수록, $f$와 $g$는 가까워지고, 당연히 무한히 미분이 가능하면 $f(x) = g(x)$라고 볼 수 있다. 무한번 미분이 가능해진 상황에서는 더이상 $a$는 중요하지 않다. 따라서 매클로린 급수를 함수 $f$와 같다고 생각해버릴 수도 있다. (억지로 찾으면 아닌 경우도 있다. 하지만 난 수학과가 아니다.)

아무튼 우리는 이제 식 9를 이용해 대충 어떤 함수를 다항식으로 근사해버릴 수 있다. 직접 해보자.

사용 사례

---

위의 식 9를 이용하면 어떤 함수 $f$에 대해서 $x=a$ 근방의 근사식을 구할 수 있다. 사실 위에서 나온 $\sin x$ 의 그래프도 식 9를 이용한 결과다.

이번엔 대충 아무런 적당히 복잡한 함수 하나 해보자 .

아는 사람들은 알겠지만, 이 함수는 일반적인 방법으로 적분을 구할 수 없다. 궁금하면 오차함수, 가우스 적분 등에 대해 검색해보자.

근데 이 $f(x)$는 사실 미분은 엄청 쉽다. 즉, 매클로린 급수의 형태로 쉽게 나타낼 수 있다. 식 9를 적용하면 아래와 같다. 굳이 계산 과정을 넣진 않겠다.

이 $g(x)$의 적분은 이제 고등학생도 할 수 있다. 즉, $f(x)$를 적분할 수 있게 되었다. 이것도 굳이 결과가 중요한 것은 아니라 생략한다.

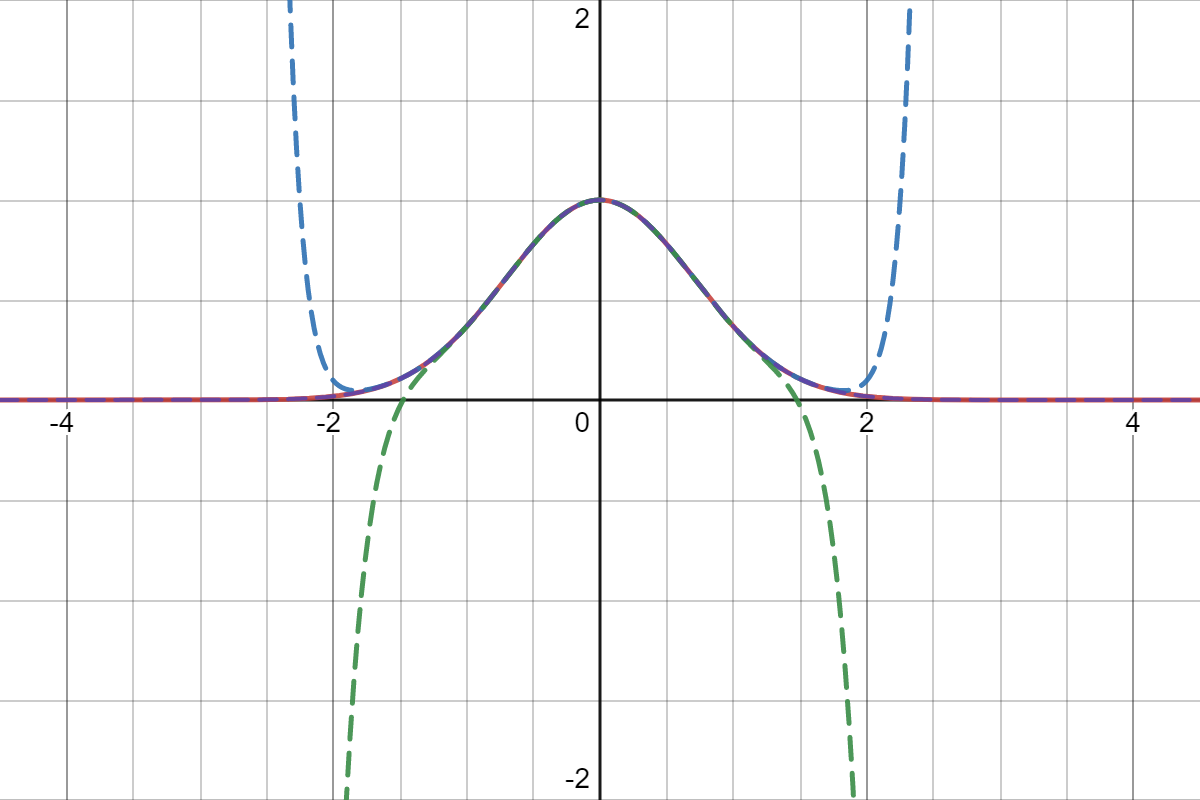
위 $g(x)$, 식 11에 대해 $n=5, 10, 200$까지인 경우에 대해 그래프를 한번 그려봤다.

$f(x)$는 빨간색 선, $n=5, 10, 200$ 은 순서대로 초록, 파랑, 보라색 선이다. 보라색 선은 거의 완전히 겹쳐버린 모습이다.

다른 간단한 예시로는 물리학에서 $x \approx 0$ 일 때 $\sin x \approx x$ 라고 생각하는 경우가 있다. 식 9를 이용해보면 $\sin x$의 매클로린 급수의 일차식은 $x$고, 이것을 바로 이용하는 형태다. 제일 처음에 그린 그래프를 보면 뭐 나쁘지는 않아 보인다. 이렇게 일차식을 이용하는 경우를 First-order Taylor Series 라고 한다. 너무 당연하게 이차식까지 쓰면 Second-order Taylor Series 다.