알고리즘 복잡도 계산이 필요한 이유

---

• 하나의 문제를 푸는 알고리즘은 여러가지가 있을 수 있다.
  • 예를들어, 정수의 절대값을 구하는 문제(1, -1 -> 1)
    • solve1) 정수값을 제곱한 다음 루트를 사용하기
    • solve2) 정수값이 음수인지 양수인지 판별한 다음 음수일 때 -1 곱하기
• 다양한 알고리즘 중에서 어느 알고리즘이 이 문제를 풀 때 더 좋은지 분석하기 위해 복잡도를 계산한다.

알고리즘 복잡도 계산 항목

---

• 시간 복잡도 : 알고리즘의 절대적인 실행 시간이 아닌 알고리즘을 수행하는데 연산들이 몇 번 이루어지는 지 숫자로 표기한다.
• 공간 복잡도 : 프로그램을 실행시킨 후 완료하는 데 필요로 하는 자원 공간의 양을 의미한다.

알고리즘 시간 복잡도의 주요 요소

---

시간 복잡도에 가장 영향을 많이 미치는 요소는 반복문이다!!

알고리즘 성능 표기법

---

• Big O(빅 오) 표기법 : O(n)
  • 알고리즘 최악의 실행 시간을 표기한다.
  • 일반적으로 가장 많이 사용한다.
• Ω (오메가) 표기법 : Ω(n)
  • 알고리즘 최상의 실행 시간을 표기한다.
• Θ (세타) 표기법 : Θ(n)
  • 알고리즘 평균 실행 시간을 표기한다.

빅 오 표기법

---

• 입력 n에 따라 결정되는 시간 복잡도 함수이다.
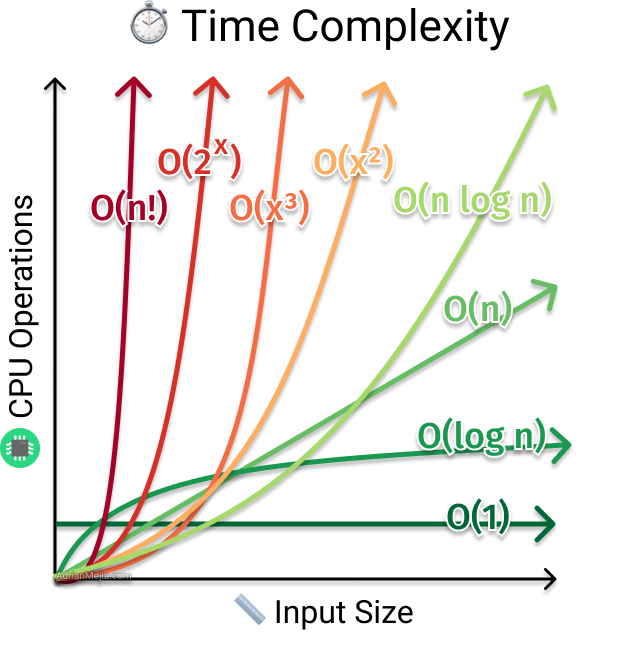
• O(1) < O($log n$) < O(n) < O(n$log n$) < O($n^2$) < O($2^n$) < O(n!)
  • 맨 위의 이미지를 보자!

빅 오 표기법의 특징

• 상수항을 무시한다.
  • 빅 오 표기법은 데이터 입력값(n)이 충분히 크다고 가정하고 있고, 알고리즘 효율성 또한 데이터 입력값의 크기에 따라 영향 받기 때문에 상수항 같은 사소한 부분은 무시한다.
  • O(2n) -> O(n)과 같이 상수항은 무시하고 표기한다.
• 영향력 없는 항은 무시한다.
  • 가장 영향력이 큰 항 외에는 무시한다.
  • O($n^2$ + 2n + 1) -> O($n^2$)과 같이 영향력이 없는 항들은 무시한다.