힙(Heap)

---

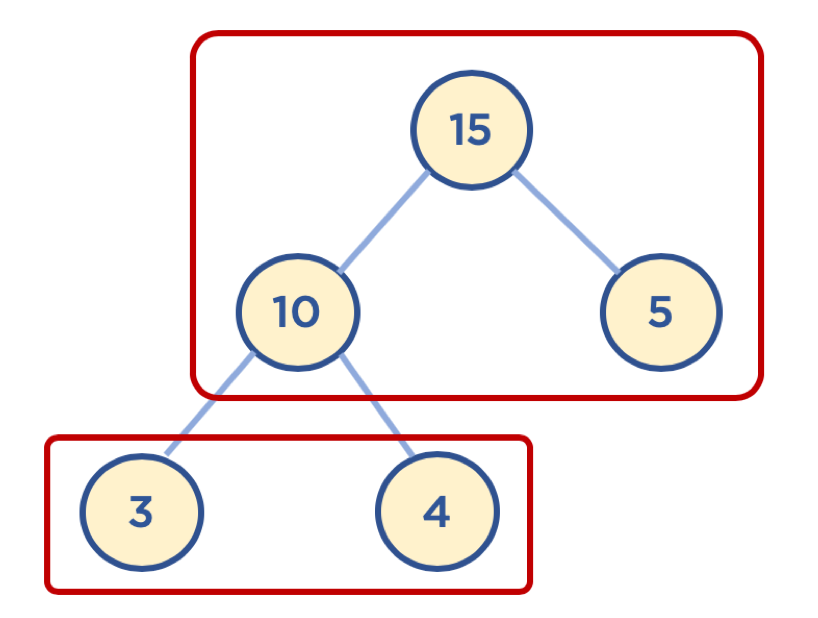
• 힙(Heap) : 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리이다.
  • 완전 이진 트리 : 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리이다.
• 힙을 사용하는이유
  • 배열에 데이터를 넣고, 최대값과 최소값을 찾으면 $O(n)$이 걸린다.
  • 힙에 데이터를 넣고, 최대값과 최소값을 찾으면 $O(logn)$이 걸린다.
  • 우선순위 큐와 같이 최대값, 최소값을 빠르게 찾아야 하는 자료구조 및 알고리즘 구현에 활용된다.

힙 구조와 시간 복잡도

---

• 힙은 최대값을 구하기 위한 구조(Max Heap)와 최소값을 구하기 위한 구조(Min Heap)로 분류 된다.
• 힙은 두 가지 조건을 가지고 있는 자료구조이다.
  1. 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나(작거나) 같다.
  2. 완전 이진 트리 형태를 가진다.

시간 복잡도

힙(Heap)의 노드가 n개라면, 트리의 높이(Depth)인 $h=log_2n$에 수렴한다.
즉, 시간 복잡도는 $O(logn)$이다.

힙과 이진 탐색 트리의 공통점과 차이점

---

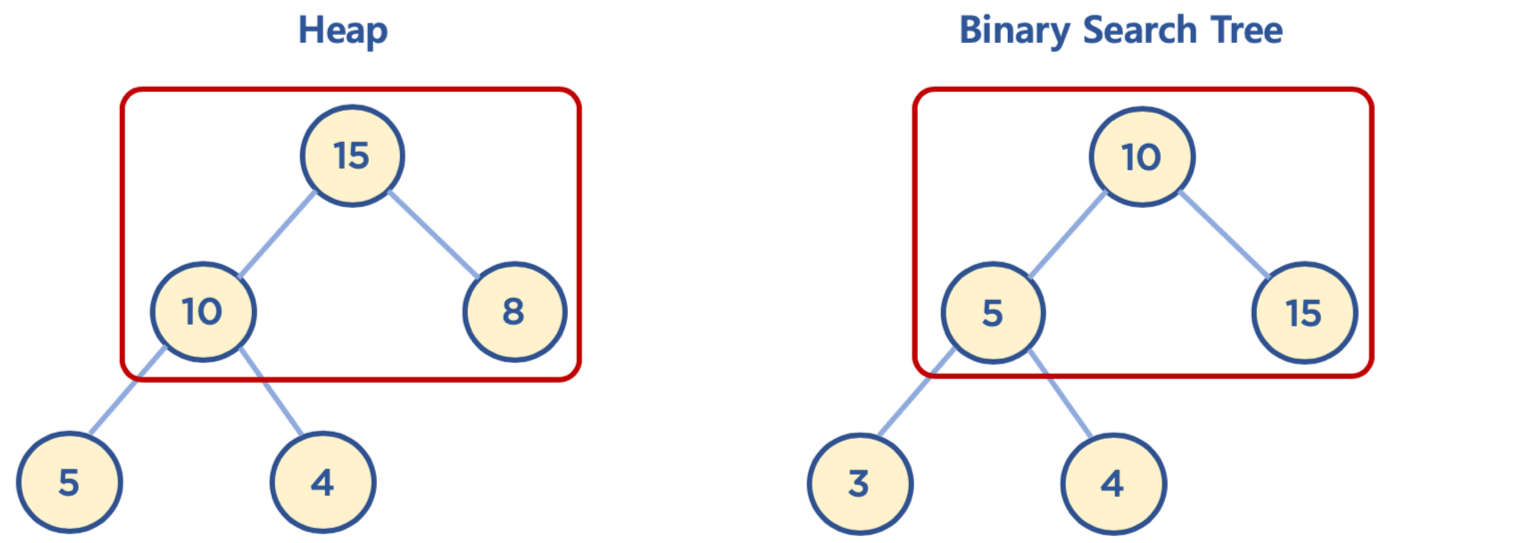
• 공통점 : 힙과 이진 탐색 트리 모두 이진 트리이다.
• 차이점
  • 힙은 각 노드의 값이 자식 노드보다 크거나(작거나) 같다.
  • 이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고, 부모 노드 오른쪽 자식 노드 순으로 크다.
  • 힙은 왼쪽 자식 노드가 오른쪽 자식 노드보다 클 수도 있고, 작을 수도 있다.
• 이진 탐색 트리는 탐색을 위한 구조, 힙은 최대값, 최소값 검색을 위한 구조로 생각하면 된다.

힙 동작

---

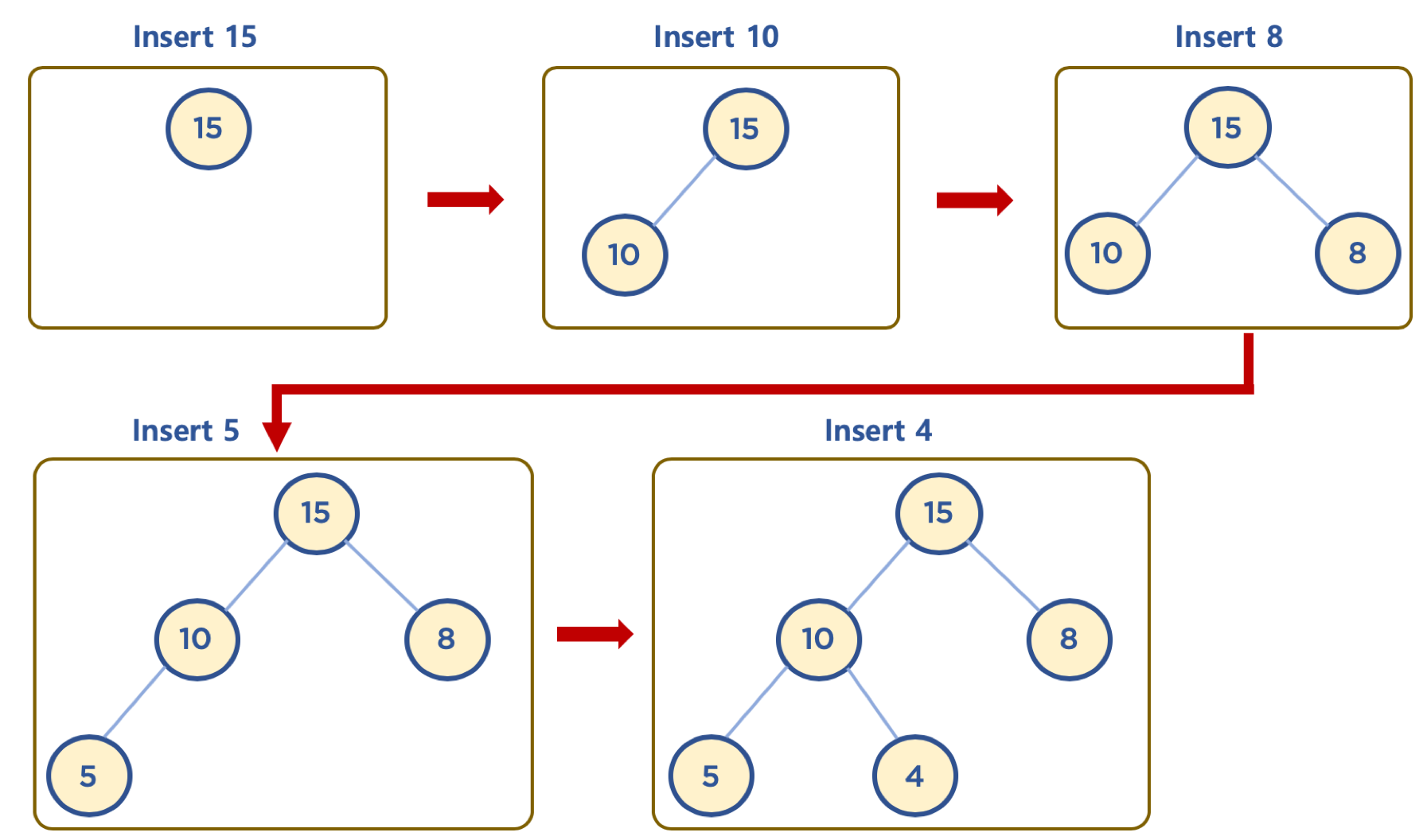
힙에 데이터 삽입하기

기본 동작

• 힙은 완전 이진 트리이므로 삽입할 노드는 기본적으로 왼쪽 최하단 노드부터 채워진다.
  

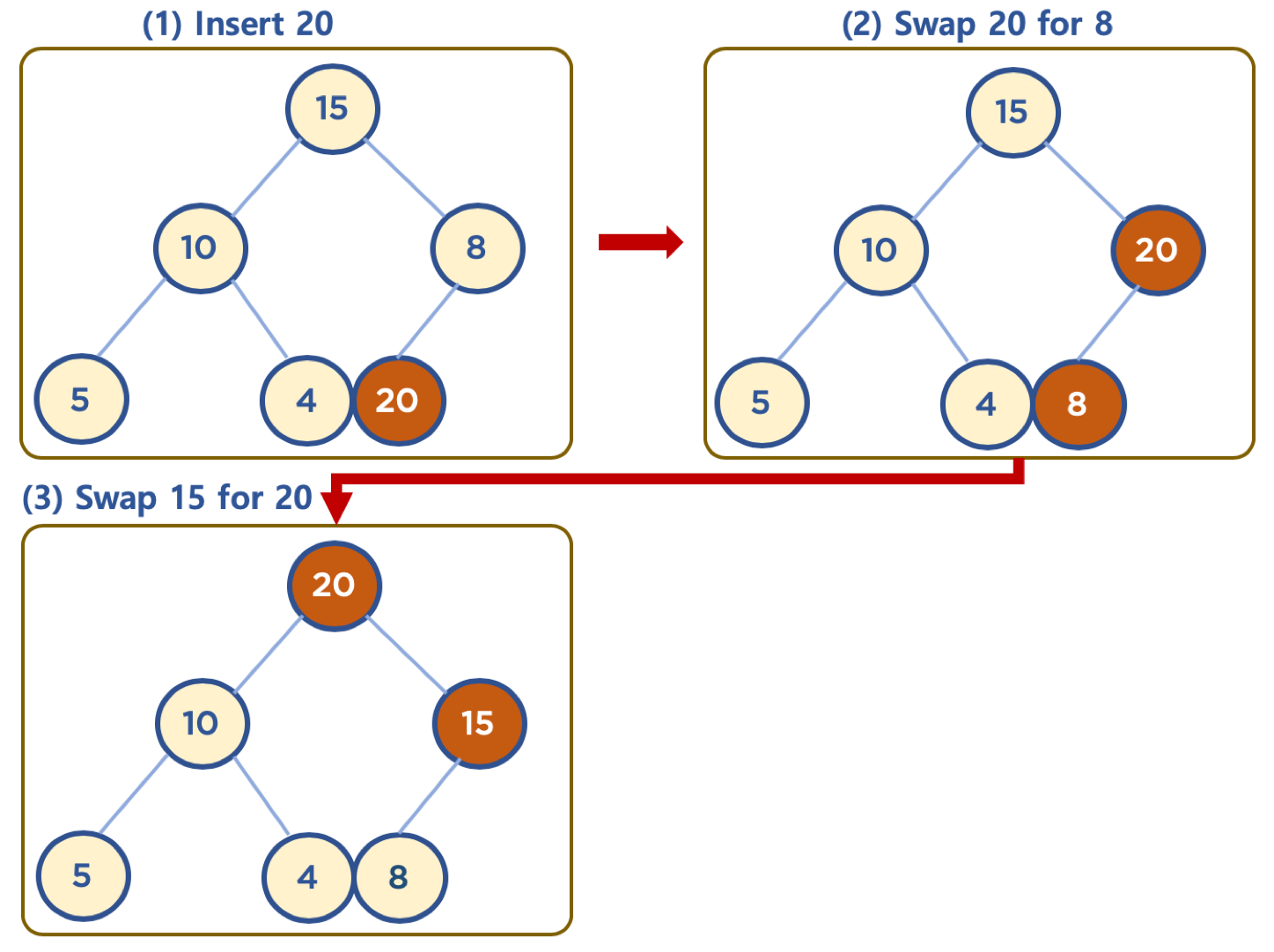
삽입할 데이터가 힙의 데이터보다 클 경우(Max Heap)

• 삽입된 데이터는 완전 이진 트리 구조에 맞추어, 왼쪽 최하단 노드부터 채워진다.
• 삽입된 노드 위치에서 부모 노드보다 값이 클 경우, 부모 노드와 위치를 바꿔주는 작업을 반복한다.
  

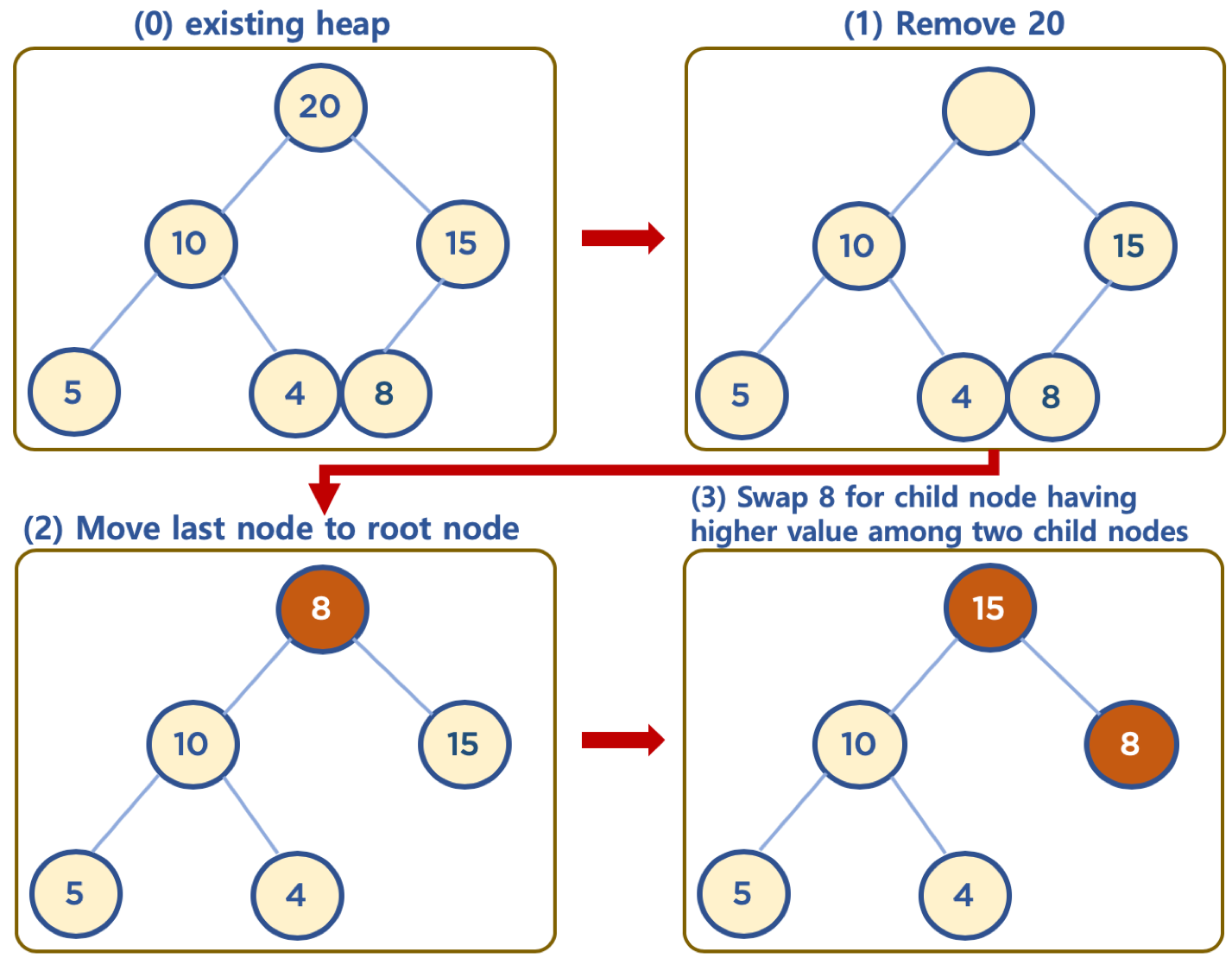
힙에 데이터 삭제하기

• 힙의 용도는 최대값, 최소값을 루트 노드에 놓아서 바로 꺼내 쓸 수 있도록 하기 위함이다.
  그래서 보통 삭제는 루트 노드를 삭제한다.
• 루트 노드의 데이터 삭제 시, 가장 마지막에 추가한 노드를 루트 노드로 이동한다.
• 루트 노드의 값이 자식 노드보다 작을 경우, 루트 노드의 자식 노드 중에서 가장 큰 값을 가진 노드와 위치를 바꿔주는 작업을 반복한다.
  

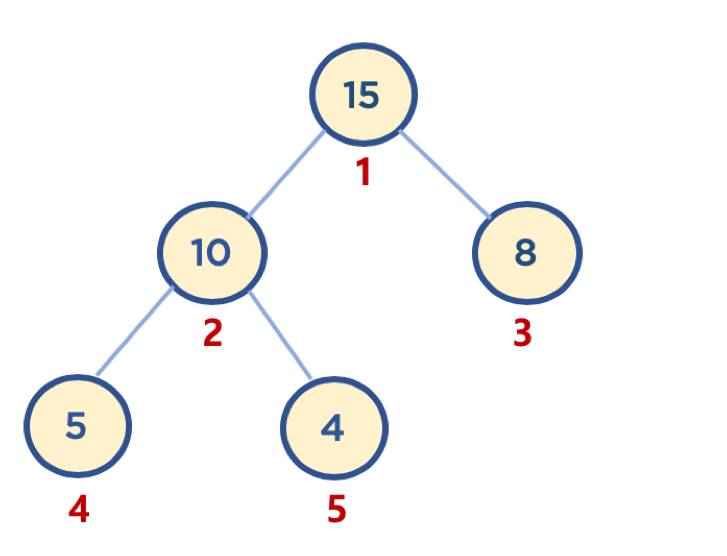
힙 구현(Max Heap)

---

• 보통 힙 구현시 배열 자료구조를 활용한다.(완전 이진 트리 구조를 가지기 때문에 가능하다.)
• 배열은 인덱스가 0번부터 시작하지만, 힙 구현을 수월하게 하기 위해 루트 노드를 1번으로 지정한다.
  • 부모 노드 인덱스 = 자식 노드 인덱스 // 2
  • 왼쪽 자식 노드 인덱스 = 부모 노드 인덱스 * 2
  • 오른쪽 자식 노드 인덱스 = 부모 노드 인덱스 * 2 + 1
    

힙에 데이터 삽입

class Heap:
    def __init__(self, data):
        self.heap_array = list()
        # 1번 인덱스가 루트 노드
        self.heap_array.append(None)
        self.heap_array.append(data)
        
    # 추가한 노드의 값이 부모 노드의 값보다 큰지 작은지 확인하는 함수
    def move_up(self, inserted_idx):
        # 루트 노드일 경우
        if inserted_idx <= 1:
            return False
        
        parent_idx = inserted_idx // 2
        if self.heap_array[inserted_idx] > self.heap_array[parent_idx]:
            return True
        else:
            return False
        
    # 힙에 데이터를 추가하는 함수
    def insertData(self, data):
        if len(self.heap_array) == 0:
            self.heap_array.append(None)
            self.heap_array.append(data)
            return True
        else:
            self.heap_array.append(data)
        
        inserted_idx = len(self.heap_array) - 1
        
        # 추가한 노드의 값이 부모 노드의 값보다 크면 값을 바꿔준다.
        while self.move_up(inserted_idx):
            parent_idx = inserted_idx // 2
            self.heap_array[inserted_idx], self.heap_array[parent_idx] = self.heap_array[parent_idx], self.heap_array[inserted_idx]
            inserted_idx = parent_idx
        
        return True

테스트

heap = Heap(15)
heap.insertData(10)
heap.insertData(8)
heap.insertData(5)
heap.insertData(4)
heap.insertData(20)
print(heap.heap_array)

# 출력
[None, 20, 10, 15, 5, 4, 8]

힙의 데이터 삭제

• 힙의 용도는 최대값, 최소값을 루트 노드에 놓아서 바로 꺼내 쓸 수 있도록 하는 것이기 때문에 루트 노드를 삭제한다.
• 루트 노드의 데이터를 삭제할 때, 마지막에 추가한 노드를 루트 노드로 이동시킨다.
  • 루트 노드의 값이 자식 노드보다 작을 경우 자식 노드 중 가장 큰 값을 가진 노드와 값을 바꾸는 작업을 한다.

class Heap:
    def __init__(self, data):
        self.heap_array = list()
        # 1번 인덱스가 루트 노드
        self.heap_array.append(None)
        self.heap_array.append(data)

    # 노드의 값이 자식 노드의 값보다 큰지 작은지 확인하는 함수
    def move_down(self, popped_idx):
        left_node_idx = popped_idx * 2
        right_node_idx = popped_idx * 2 + 1

        # 1. 왼쪽, 오른쪽 자식 노드가 없을 경우
        if left_node_idx >= len(self.heap_array):
            return False
        # 2. 왼쪽 자식 노드만 있을 경우
        elif right_node_idx >= len(self.heap_array):
            if self.heap_array[popped_idx] < self.heap_array[left_node_idx]:
                return True
            else:
                return False
        # 3. 왼쪽, 오른쪽 자식 노드가 모두 있을 경우
        else:
            if self.heap_array[left_node_idx] > self.heap_array[right_node_idx]:
                if self.heap_array[popped_idx] < self.heap_array[left_node_idx]:
                    return True
                else:
                    return False
            else:
                if self.heap_array[popped_idx] < self.heap_array[right_node_idx]:
                    return True
                else:
                    return False

    # 힙의 데이터를 삭제하는 함수
    def popData(self):
        if len(self.heap_array) <= 1:
            return None

        returned_data = self.heap_array[1]
        popped_idx = 1
        # 마지막에 추가한 노드를 루트 노드로 옮긴다.
        self.heap_array[popped_idx] = self.heap_array.pop()

        while self.move_down(popped_idx):
            left_node_idx = popped_idx * 2
            right_node_idx = popped_idx * 2 + 1

            # 왼쪽 노드만 있을 경우
            if right_node_idx >= len(self.heap_array):
                if self.heap_array[popped_idx] < self.heap_array[left_node_idx]:
                    self.heap_array[popped_idx], self.heap_array[left_node_idx] = self.heap_array[left_node_idx], self.heap_array[popped_idx]
                    popped_idx = left_node_idx

            # 왼쪽, 오른쪽 노드 모두 있을 경우
            else:
                if self.heap_array[left_node_idx] > self.heap_array[right_node_idx]:
                    if self.heap_array[popped_idx] < self.heap_array[left_node_idx]:
                        self.heap_array[popped_idx], self.heap_array[left_node_idx] = self.heap_array[left_node_idx], self.heap_array[popped_idx]
                        popped_idx = left_node_idx
                else:
                    if self.heap_array[popped_idx] < self.heap_array[right_node_idx]:
                        self.heap_array[popped_idx], self.heap_array[right_node_idx] = self.heap_array[right_node_idx], self.heap_array[popped_idx]
                        popped_idx = right_node_idx

        return returned_data

테스트

heap = Heap(15)
heap.insertData(10)
heap.insertData(8)
heap.insertData(5)
heap.insertData(4)
heap.insertData(20)
print(heap.heap_array)
heap.popData()
print(heap.heap_array)

# 출력
[None, 20, 10, 15, 5, 4, 8]
[None, 15, 10, 8, 5, 4]

전체 코드

class Heap:
    def __init__(self, data):
        self.heap_array = list()
        # 1번 인덱스가 루트 노드
        self.heap_array.append(None)
        self.heap_array.append(data)

    # 추가한 노드의 값이 부모 노드의 값보다 큰지 작은지 확인하는 함수
    def move_up(self, inserted_idx):
        if inserted_idx <= 1:
            return False

        parent_idx = inserted_idx // 2
        if self.heap_array[inserted_idx] > self.heap_array[parent_idx]:
            return True
        else:
            return False

    # 노드의 값이 자식 노드의 값보다 큰지 작은지 확인하는 함수
    def move_down(self, popped_idx):
        left_node_idx = popped_idx * 2
        right_node_idx = popped_idx * 2 + 1

        # 1. 왼쪽, 오른쪽 자식 노드가 없을 경우
        if left_node_idx >= len(self.heap_array):
            return False
        # 2. 왼쪽 자식 노드만 있을 경우
        elif right_node_idx >= len(self.heap_array):
            if self.heap_array[popped_idx] < self.heap_array[left_node_idx]:
                return True
            else:
                return False
        # 3. 왼쪽, 오른쪽 자식 노드가 모두 있을 경우
        else:
            if self.heap_array[left_node_idx] > self.heap_array[right_node_idx]:
                if self.heap_array[popped_idx] < self.heap_array[left_node_idx]:
                    return True
                else:
                    return False
            else:
                if self.heap_array[popped_idx] < self.heap_array[right_node_idx]:
                    return True
                else:
                    return False

    # 힙에 데이터를 추가하는 함수
    def insertData(self, data):
        if len(self.heap_array) == 0:
            self.heap_array.append(None)
            self.heap_array.append(data)
            return True
        else:
            self.heap_array.append(data)

        inserted_idx = len(self.heap_array) - 1

        # 추가한 노드의 값이 부모 노드의 값보다 크면 값을 바꿔준다.
        while self.move_up(inserted_idx):
            parent_idx = inserted_idx // 2
            self.heap_array[inserted_idx], self.heap_array[parent_idx] = self.heap_array[parent_idx], self.heap_array[inserted_idx]
            inserted_idx = parent_idx
        return True

    # 힙의 데이터를 삭제하는 함수
    def popData(self):
        if len(self.heap_array) <= 1:
            return None

        returned_data = self.heap_array[1]
        popped_idx = 1
        # 마지막에 추가한 노드를 루트 노드로 옮긴다.
        self.heap_array[popped_idx] = self.heap_array.pop()

        while self.move_down(popped_idx):
            left_node_idx = popped_idx * 2
            right_node_idx = popped_idx * 2 + 1

            # 왼쪽 노드만 있을 경우
            if right_node_idx >= len(self.heap_array):
                if self.heap_array[popped_idx] < self.heap_array[left_node_idx]:
                    self.heap_array[popped_idx], self.heap_array[left_node_idx] = self.heap_array[left_node_idx], self.heap_array[popped_idx]
                    popped_idx = left_node_idx

            # 왼쪽, 오른쪽 노드 모두 있을 경우
            else:
                if self.heap_array[left_node_idx] > self.heap_array[right_node_idx]:
                    if self.heap_array[popped_idx] < self.heap_array[left_node_idx]:
                        self.heap_array[popped_idx], self.heap_array[left_node_idx] = self.heap_array[left_node_idx], self.heap_array[popped_idx]
                        popped_idx = left_node_idx
                else:
                    if self.heap_array[popped_idx] < self.heap_array[right_node_idx]:
                        self.heap_array[popped_idx], self.heap_array[right_node_idx] = self.heap_array[right_node_idx], self.heap_array[popped_idx]
                        popped_idx = right_node_idx

        return returned_data