[BOJ]1504(python)

BOJ - 1504(특정한 최단거리) python 풀이

어떻게 풀어야 하지?

맨 처음에는 그냥 최단거리를 구하면 되는거 아닌가? 하고 저번에 쓴 최소 스패닝을 이용해서 풀이하려고 했는데...

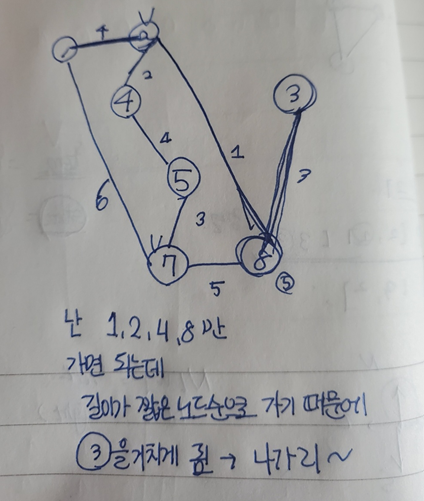
그럴 경우에는 경로를 구할 때 굳이 지나지 않아도 되는 노드를 지나야 했기 때문에 맞지 않다고 생각했습니다

(안녕!)

그래서 1 -> a, a -> b, b -> N 노드의
최단 거리를 각각 구할 수 있는 다익스트라를 이용해서 풀이하기로 했습니다

다익스트라란?

한 정점에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘입니다

하나의 노드에 연결되어 있는 다음 노드들의 가중치들을 갱신하는 방식으로 풀 수 있고 이 문제에서는 저희가 지정한 각 정점간의 최단거리만 구하면 될 것이라고 생각했습니다!

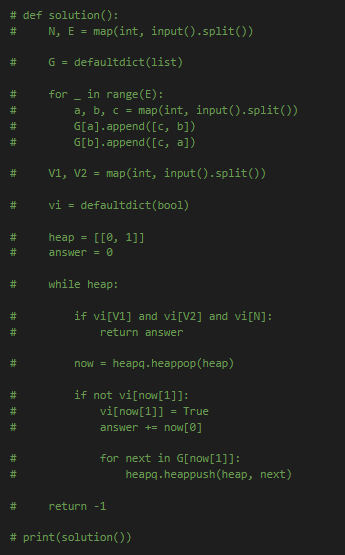
저는 힙을 이용한 다익스트라 풀이를 했습니다

코드

from collections import defaultdict
import heapq

def solution():

    N, E = map(int, input().split())
    G = defaultdict(list)

    for _ in range(E):
        a, b, c = map(int, input().split())
        G[a].append([c, b])
        G[b].append([c, a])
    
    V1, V2 = map(int, input().split())

    def dijk(start, end):

        nonlocal G, N
        D = defaultdict(lambda : float('INF'))
        visited = defaultdict(bool)
        heap = [[0, start]] #처음 

        while heap:

            now = heapq.heappop(heap)

            if not visited[now[1]]:
                visited[now[1]] = True
                if D[now[1]] > now[0]:
                    D[now[1]] = now[0]

                for next in G[now[1]]:
                    n_c = next[0] + D[now[1]]
                    if D[next[1]] > n_c:
                        D[next[1]] = n_c
                        heapq.heappush(heap, [n_c, next[1]])
        
        return D[end]


    answer = min(dijk(1, V1) + dijk(V1, V2) + dijk(V2, N), dijk(1, V2) + dijk(V2, V1) + dijk(V1, N))

    if answer == float('INF'): print(-1)
    else: print(answer)

solution()

1. 연결 정보들을 저장해줍니다. 이 때 저는 우선순위큐를 편하게 이용하기 위해서 [거리, 노드] 순서로 저장을 했습니다

2. 최단거리로 갈 수 있는 순서가 아래와 같이 두개가 있어서 둘 중 작은 값을 구해줍니다

   • 1번 -> V1 노드 -> V2 노드 -> N
   • 1번 -> V2 노드 -> V1 노드 -> N
   • 각각을 코드로 표현하면 아래와 같습니다

   dijk(1, V1) + dijk(V1, V2) + dijk(V2, N)
   dijk(1, V2) + dijk(V2, V1) + dijk(V1, N)

3. 다익스트라 코드는 다음과 같이 작성했습니다

   • 모든 노드간 거리를 float('INF') 최댓값으로 초기화 했습니다
   • [현재 거리(0), 현재 노드(start)]로 우선순위큐를 초기화 했습니다
   • 큐에서 가장 거리가 짧은 노드를 꺼내주고 현재의 노드를 방문하지 않았다면 방문처리를 해주고 다음 과정을 반복합니다
     • 기존의 거리가 현재 거리보다 클 경우 지금 거리로 초기화 해줍니다(작은 값으로 초기화)
     • 이후 연결된 노드들에 대해서도 같은 작업을 반복합니다
     • 우선순위큐에 [현재 노드의 거리 + 다음노드까지의 거리, 다음노드] 정보를 추가합니다
   • 이후 목적지의 거리 값을 return 합니다
     

4. 만일 1번에 있던 값이 float('INF')로 초기화 되지 않았다면, 목적지에 도착할 수 없다는 뜻이기 때문에 -1을 return 합니다

풀이 하면서 있던 승질나는 일 (물론 내 잘못)

next에서 다음 값을 따로 만들기가 귀찮아서
아래처럼 코드를 짰더니

for next in G[now[1]]:
	next[0] += D[now[1]]
    
    if D[next[1]] > next[0]:
    	D[next[1]] = next[0]
        heapq.heappush(heap, next)

앞의 값이 뒤의 값에 영향을 줘서 애를 먹었습니다 하하..
python도 객체지향이여서 그런가봐요
(아무튼 멍청비용으로 40분 날려먹음)
다음부터는 그러지 말아야겠습니다