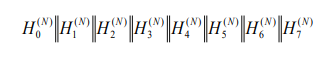정의
- 미국 국립표준기술연구소(NIST)에서 공표된 표준 해시 알고리즘인 MD와 SHA 중 SHA-2 계열에 속하는 알고리즘이며 현재 블록체인에서 가장 많이 채택해 사용되고 있는 암호 방식.
- 256비트로 구성되며 64자리 문자열을 반환하는데 쉽게 말해 어떤 길이의 값을 입력해도 256비트의 고정된 결과값을 출력한다.
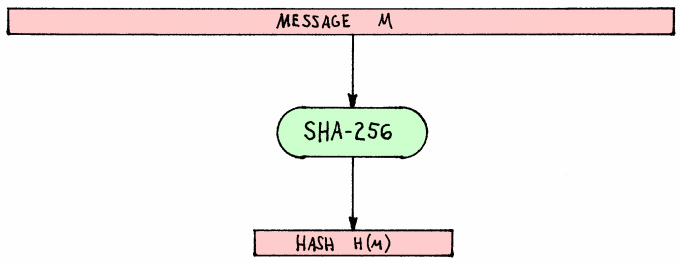
동작원리
1. 전처리 단계
1) 확장(padding)

예를 들어 "abc"라는 문자열을 SHA-256을 이용해 해시코드로 변환하려 한다면 우리는 이 문자열의 크기를 512bit로 확장(padding) 한 후 입력값으로 넣어야 한다.
문자 하나당 1byte, 즉 8bit를 차지하게 만들어 "abc"라는 문자열은 총 24bit가 되는데 우선 이를 이진법으로 나타내면 0110001 0110010 01100011 이 된다.
먼저 이 바로 뒤에 1bit 를 추가한다
그리고 512bit가 되도록 그 뒤에 쭉 0을 추가하는데 마지막 64bit엔 원래 문자열의 길이 즉 24bit를 적는다.
이렇게 확장한 512bit의 문자열이 SHA-256의 입력값이 된다.
2)분리(parsing)
"abc"라는 문자열을 512bit로 확장시킨 후 이걸 다시 32bit씩 16개로 나눈다.
2. 해싱 단계
이제 앞에서 하나의 message를 전처리 단계를 거쳐 한 블록을 16개의 32bit 크기를 가진 값으로 차례로 W0~W15까지라 하고 추가적으로
W16~W63까지 총 48개는 특정 계산법을 사용해 만들어 한 블록당 총 64개 의 W로 나누고
H와 K라는 상수를 구해 총 H, W, K 이 3가지 값을 Round fuction이라는 핵심 함수의 인자로 사용하여 한 블록당 64 round 진행하여 최종 결과값으로 나온 H는 다음 블록의 초기 H값으로 들어가고 그렇게 나온 최종 H가 우리가 구하려는 해시값이 된다.
- 위에서 예시로 든 "abc"는 전처리 단계를 거쳐 512bit, 즉 한 블록만 나왔으므로 전체적으로 64번의 round함수를 진행한다.
아래 그림이 해싱 단계의 전체적인 과정을 그림으로 나타낸 것이고 이를 번호순으로 차근차근 살펴보겠다.
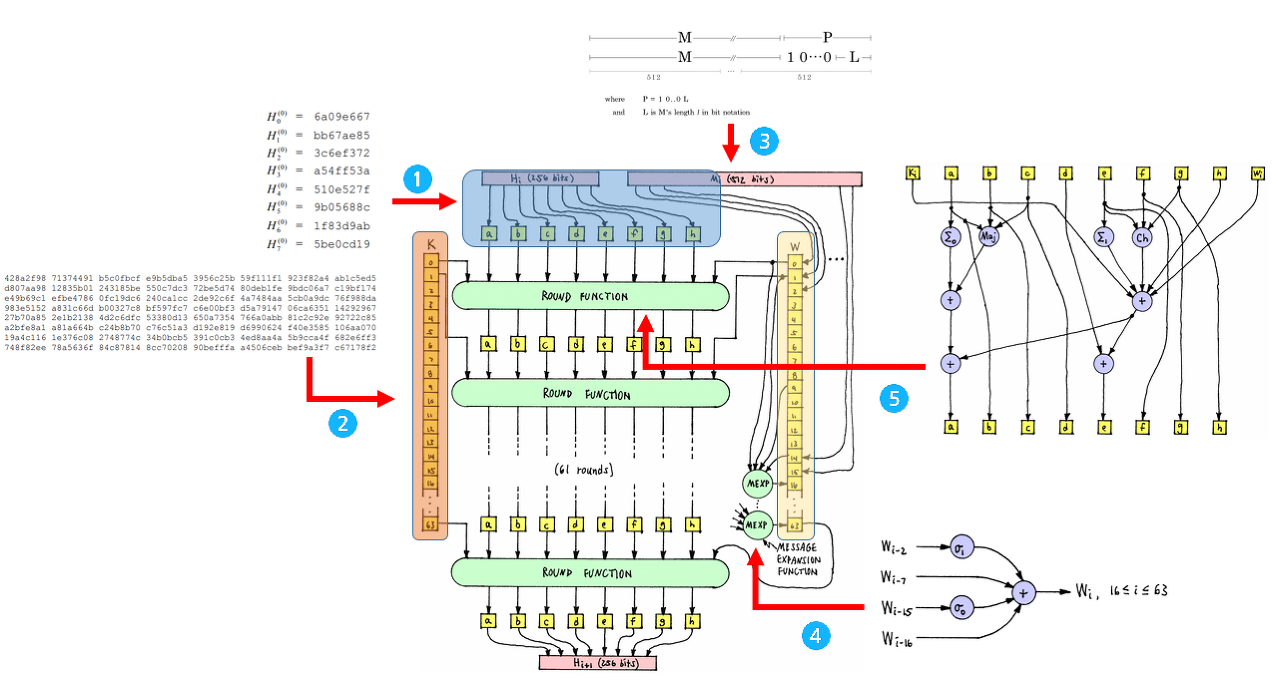
1) H 구하기
H는 256bit 크기를 가지며 32bit씩 8개로 나뉘어 Round 함수의 인자로 들어간다.
첫 번째 블록(512 bit)의 초기 H값으로 들어갈 H0는 2부터 시작하는 소수 8개 (2,3,5,7,11,13,17,19)를 루트를 씌운 후
소수점 아래자리 32비트를 추려낸 것이다. 이를 16진수로 표현하면 다음과 같다.

이 값들이 초기값으로 들어가 64번의 Round를 거친 후 나오게 된 H1~.. Hn 은 블록의 수에 따라 그다음 블록의 초기 값이 되거나 최종 해시값이 된다.
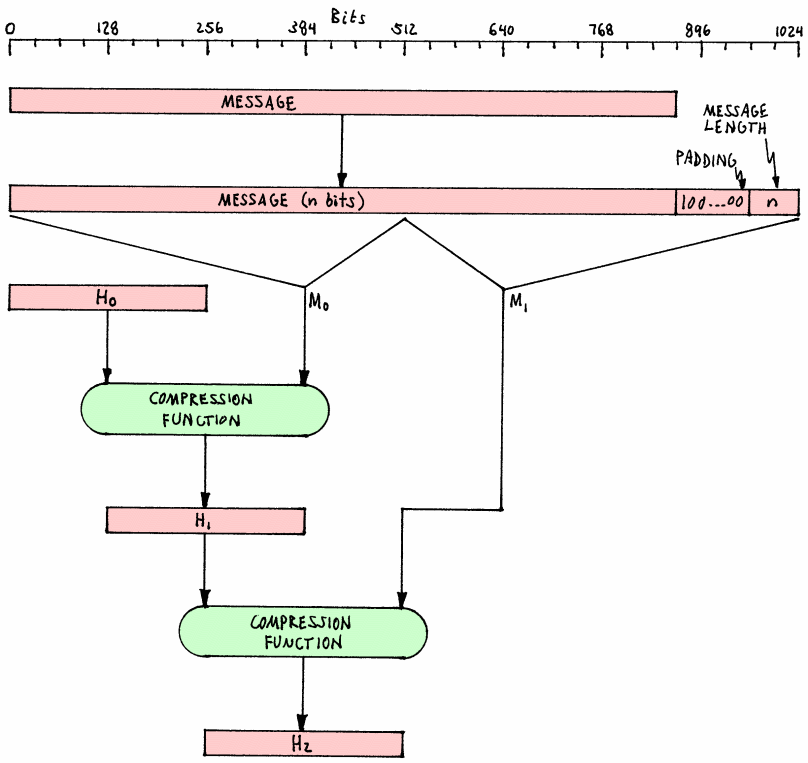
-
512bit는 넘지만 1024bit는 안되는 (512의 배수가 안 되는) 크기를 가진 message를 512의 배수가 되도록 1024bit까지 확장한 후 512bit 기준으로 두개의 블록(M0, M1)을 만든다
-
첫 번째 블록(M0)의 Compression (Round) 함수의 인자로 H0를 사용하고 64 Round를 거쳐 나온 H1은 다시 두 번째 블록(M1)의 Compression (Round) 함수의 인자가 되어 최종적으로 나온 H2가 이 message의 해시가 된다.
2) K 구하기
K 한 칸당 32 bit씩 64개의 칸을 갖고 있는 배열이며 2부터 시작하는 64개의 소수에 대해 세제곱근을 취한 뒤, 소수점 아래 32bit를 추출하면 얻을 수 있다. 이를 16진수로 표현하면 다음과 같다.

3~4) W 구하기
W는 앞서 설명한것에 덧붙여 설명하여 전처리 과정을 거친 블록, 즉 16개로 나뉜 블록들을 W0~W15까지라 하고 나머지 W16~W63 까지는 특정 계산법을 사용하여 구한다 했는데 그 계산법은 다음과 같으며
이 식을 MEXP (Message Expansion Function) 이라 부른다.
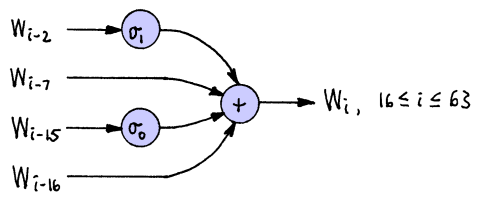
예를 들어 W16 = σ1(W14) + W9 + σ0(W1) + W0 라고 말할 수 있다.
σ0(X) = (X right-rotate 7) xor (X right-rotate 18) xor (X right-shift 3)
σ1(X) = (X right-rotate 17) xor (X right-rotate 19) xor (X right-shift 10)
5) Round Function
앞서 구한 H, K, W 이 3가지를 인자로 Round Function을 수행하면 되는데, 이 구조가 매우 복잡하지만차근차근 풀어나가면 이해할 수 있다.
아래 그림은 한 라운드에 일어나는 일을 그림으로 표현한 것이다.

먼저 우리는 전체적인 그림을 통해 ki,a,b,c,d,e,f,g,h,wi 라는 값을 입력값으로 넣고 새로운 a,b,c,d,e,f,g,h라는 출력값을 얻는 것을 확인 할 수 있다.
그리고 이때 입력값중 ki와 wi는 64번의 라운드에 하나씩 들어갈 64개의 K와 W이며
나머지 a~h는 H이고 출력으로 나온 a~h는 모든과정을 거친 새로운 H , 즉 다음 블록의 라운드함수에 이용될 초기 H이거나 message의 최종 해시가 되는 값들이다.
- 출력으로 나오는 a~h를 입력값과 비교하기 위해 '을 붙여 표현하겠다. (a',b'...)
당연히 모든 출력값은 입력값과 달라지지만 자세히 보면 계산이 필요한 값은 a'과 e'이며 나머지는 기존 값에서 옮겨지는 값임을 알 수 있다. 이를 식으로 나타내면
b' = a, c'=b, d'=c, f'=e, g'=f, h'=g
a' = (Σ0(a) + Maj(a,b,c)) + (Σ1(e) + Ch(e,f,g) + h + W0 + K0)
e' = (Σ1(e) + Ch(e,f,g) + h + W0 + K0) + d
로 나타낼 수 있다.
그럼 이제 우리가 이 식을 풀기위해 알아야할 표현은 Σ0, Σ1, Maj, Ch이다.
이를 하나씩 알아가 보면
Σ0 은 인자값을 2, 13, 22 만큼 각각 오른쪽으로 돌리고 그 세값을 비교하여 합이 홀수인 곳은 1, 0이거나 짝수인 곳은 0으로 표기한다.

Σ1 은 인자값을 6, 11, 25 만큼 각각 오른쪽으로 돌리고 그 세값을 비교하여 합이 홀수인 곳은 1, 0이거나 짝수인 곳은 0으로 표기한다.
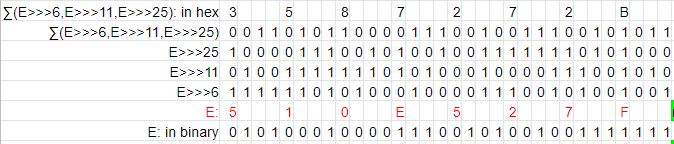
Maj 는 인자로 사용된 세 값의 같은 위치 비트가 1이 많으면 1, 0이 많으면 0이 된다.
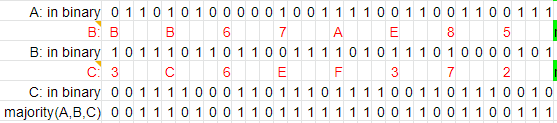
Ch 는 인자로 사용된 세 값을 a,b,c라 하면 a의 비트가 1이면 그 위치는 b의 비트로, 0이면 c의 비트를 선택한다.
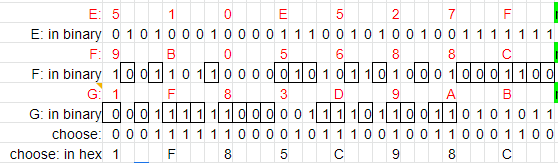
마지막으로 정리하면 입력값 Ki, Wi, H(a~h) 를 Round Function에 넣고 한 라운드당 얻게되는 결과 값을
a'~h'이라 했을 때 그 값은
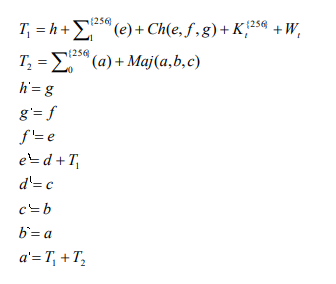
라고 표현 할 수 있으며 이과정을 64번 거치고 다음 블록이 남아있지 않아 그 값이 최종 해시값이 될 때
8개의 출력값을 H0(초기 입력값) 과 각각 더한 후 순서대로 이어붙인 16진수 값이 우리가 구하려는 해시값이 된다.
최종 H값
최종 해시값
참조 링크
https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.180-4.pdf
https://www.cs.rit.edu/~ark/lectures/onewayhash/onewayhash.shtml