그 전에는 항상 모델 기반의 데이터 프로세싱을 배워 왔다. 하지만 요새는 모델 기반의 프로세싱 보다는 데이터를 통해서 모델을 만들어 나가는 방법이 주를 이루고 있다.
Linear Regression
Linear : means that it can be graphically represented as a straight line.
1차식, 직선으로 표현 가능한
Regression : analysis is a set of statistical processes for estimating the relationships among variables.
'어떤 모델로부터 분포가 발생했는데, 이 데이터들은 그 분포의 일부다' 라고 생각해보자. 그렇다면 , 원래 이들을 나타낼 수 있는 하나의 모델이 있을 것이다. 그러면 거꾸로 이 데이터 분포를 가지고 모델을 추정할 수 있을 것이다. (데이터로부터 모델로 돌아갈 수 있을 것이다.) 따라서, 분포되어 있는 데이터를 가지고 원래 모델을 찾아가는 것을 regression 이라고 한다.
따라서, linear regression 은 모델 중에서도, 직선으로 생긴 모델을 찾아 나가는 것을 말한다.
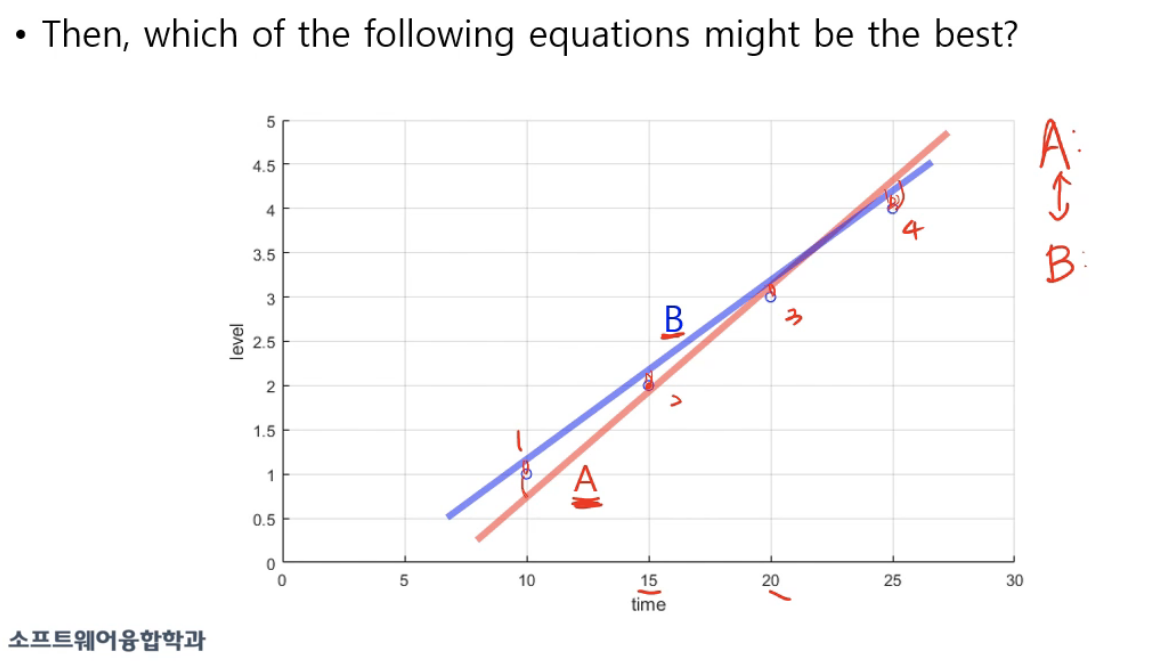
-> 기준이 없기 때문에 정답을 특정할 수 없다.
Central Limit Theorem
랜덤 변수들이 서로 모이거나 이들을 평균하면 이 분포는 정규분포를 따른다.
When independent random variables are added, their properly normalized sum tends toward a normal distribution.
Why do we use the square loss ?
- The squared error relates to Gaussian Noise.
- Assume the errors of H(x) and y are happened due to noise
- The total noise follows the Gaussian distribution by the central limit theorem.
Minimizing the least squared loss is the same as minimizing the variance of noise distribution.
Gradient Descent can only be used when the cost function is convex form
