RSDP_DNN_Neural Network
그래프는 수식과 동일하다
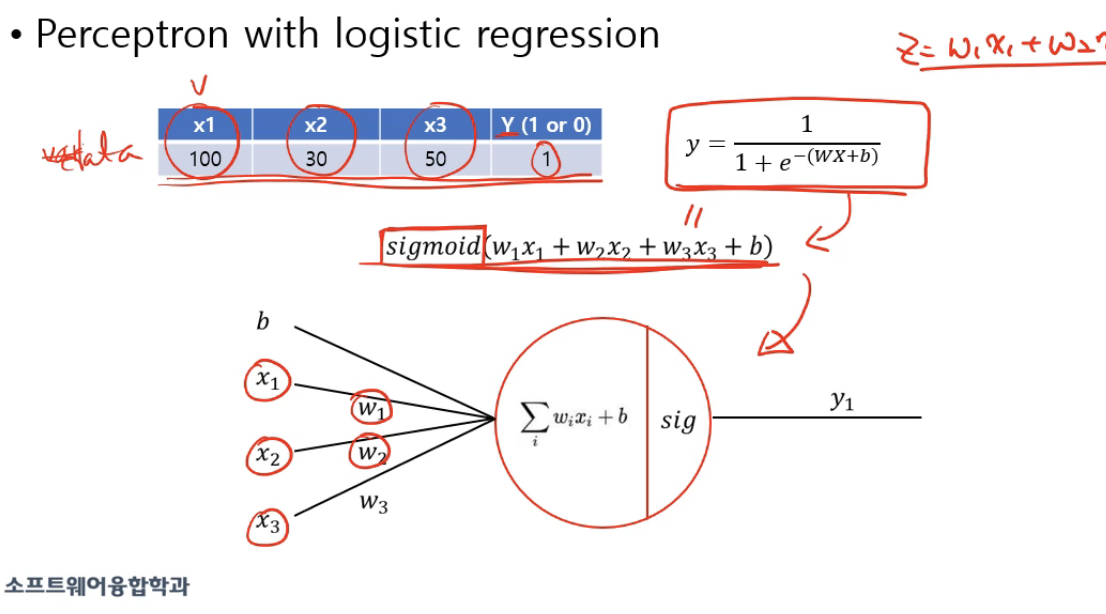
식을 정하고, 어떤 값이 들어가면 나온 값을 결과로 cost function 을 정의하고, 실제 값과의 차이로 인해 내가 지금 정한 parameter 의 값을 수정하는 과정을 반복한다.
Neural Network 는 사람의 뉴런을 모방한 perceptron 이라는 것을 만들어, 이 퍼셉트론은 여러 개의 입력을 받아 계산을 한 후 하나의 출력을 내는 것이다. 이 연산이 되는 본체는 hidden layer 이라고 한다.
그렇다면 deep 이라는 것은 무엇을 의미하는가?
hidden layer 가 2개 이상인 뉴럴 네트워크를 딥 뉴럴 네트워크라고 한다.
Softmax
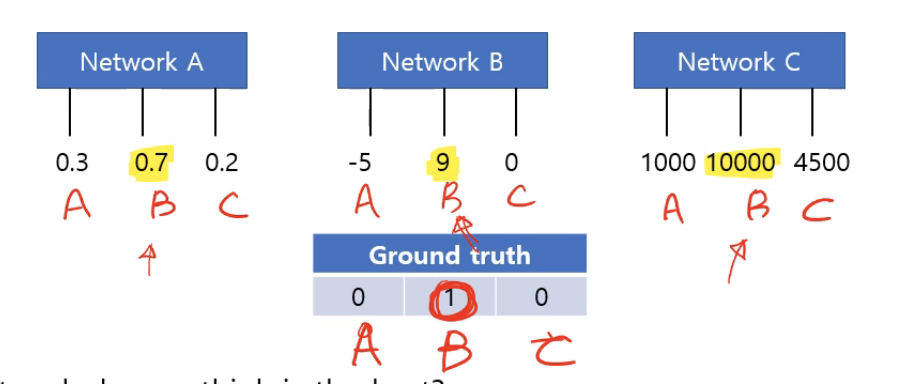
이 중에서 어떤 네트워크가 가장 좋을까?
one-hot encoding

원-핫 인코딩이란 가장 큰 값을 1로 두고 나머지를 0으로 두는 것이다.
하지만 이는 마지막에 결과를 선택할 때만 사용하며, ground truth 와 네트워크 결과값을 비교할 때는 원-핫 인코딩을 사용하지 않는다.
즉 실제로 뉴럴 네트워크를 사용하는 시점인 evaluation 단계에서 사용하며 training 단계에서는 사용하지 않는다.
We should produce output in probability domain of which sum is 1.
There are several ways to represent variables to probability.
Monotonically (단조 증가 함수) function is used.
- 결과값을 확률값으로 바꿔 보자.
결과값은 음수도 있을 수 있고 그래서 연산할 수 있게 확률변수로 바꿔주는 (정규화하는) 것이다.
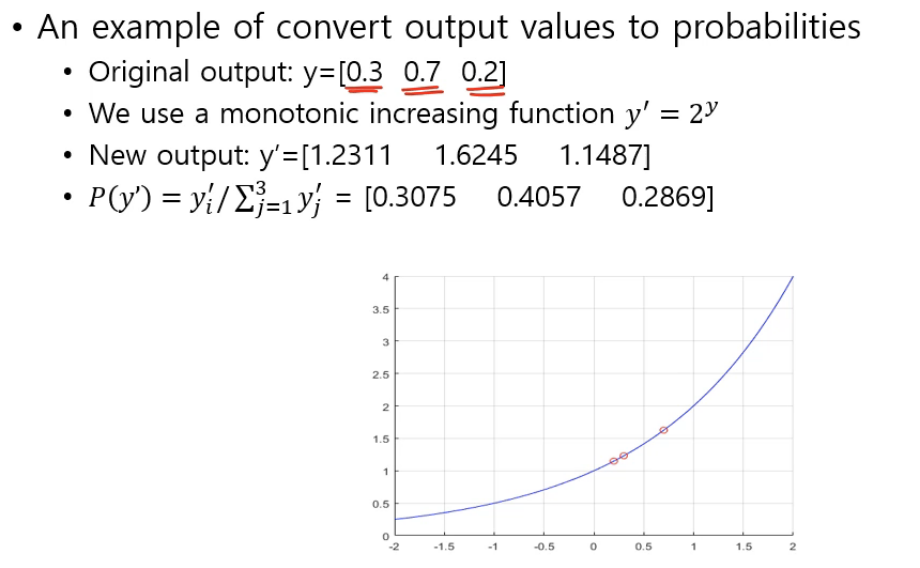
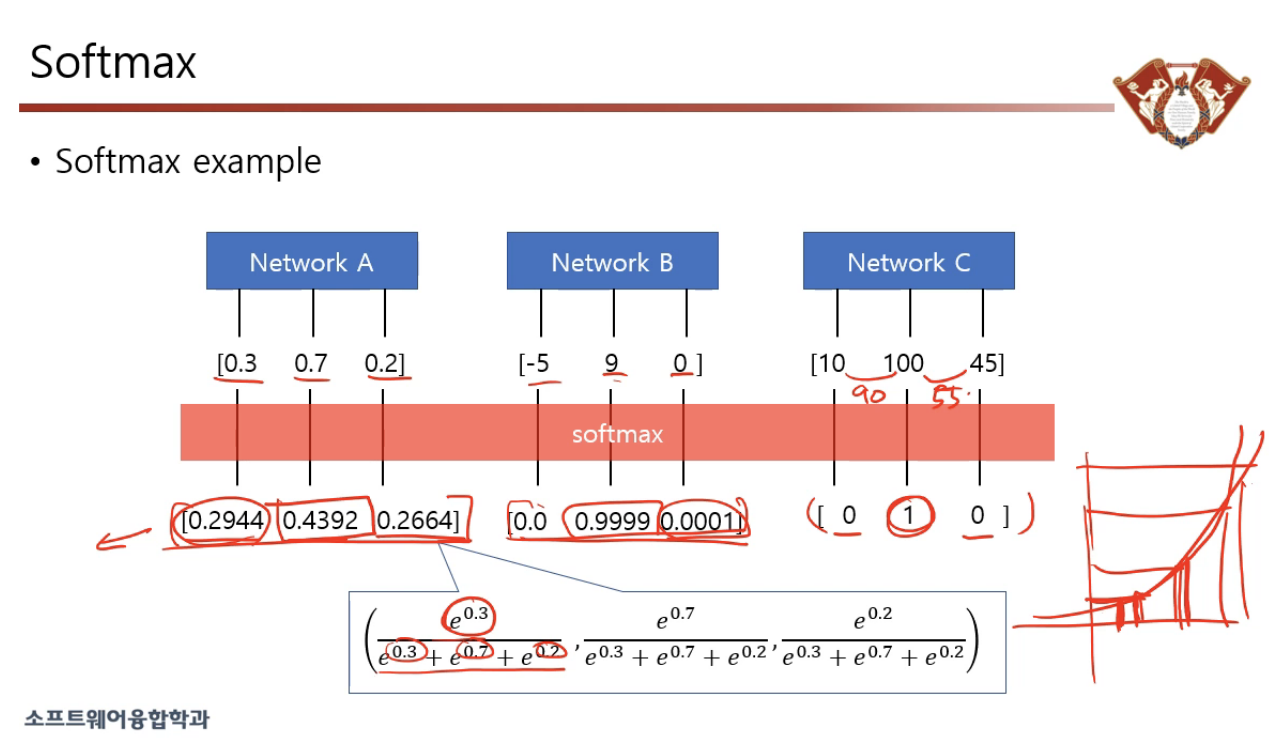
개개별의 값을 양수로 만들어줘야 하기 때문에 monotonically increasing function 중에서 지수함수를 주로 사용하고, 지수함수의 밑은 여러 개 있을 수 있지만 그 중에서도 자연로그를 밑으로 하는 지수함수에 매핑 하는 것을 softmax 라고 한다.
그렇다면 왜 e 를 밑으로 쓰는가?
Why do we use exponential as softmax function?
Answer : it follows Bayes Theorem
Cross entropy
아무튼 해야 할 것은 네트워크에서 나온 결과값을 Ground Truth 와 비교하는 작업인 것이다.
Widely used in classification

Cross Entropy 는 서로 다른 두 개의 분포를 가지고 뭔가 값을 나타낼 수 있는 방법 중 하나이다.
Entropy
네트워크에서는 정보를 전송할 때 필요한 비트 수를 나타낸다.
여기서는 정보량을 수학적으로 나타낼 때 쓰이는데,
확률이 낮을 수 록 정보량이 크다.
내일 아침에는 해가 뜰 것이다. < 내일 아침에는 해가 뜨지 않을 것이다.
엔트로피 = 정보량 x 확률


p1 의 경우 반반 = 애매함 = 엔트로피 큼
p3 의 경우 확률분포 극단적 = 안 애매함 = 엔트로피 작음
크로스 엔트로피는 서로 다른 확률 분포를 가지고 엔트로피를 구하는 것이다.

어떻게 ? => 정보량은 한 쪽에서 가져오고, 확률값은 다른 쪽에서 가져오는 것이다.
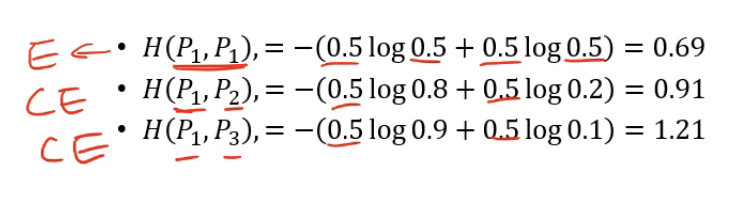
엔트로피 / 크로스 엔트로피 값이 점점 증가하는 것을 볼 수 있다. ( 두 개의 확률 분포가 다르면 확률 분포가 점점 커진다. )
두 개의 확률 분포가 다르면 무조건 엔트로피보다 크게 나온다.
KL-Divergence
두 개의 확률 분포가 얼마나 다른가를 측정하는 방법

P : Ground Truth
Q : Softmax 해서 나온 확률분포
따라서 크로스 엔트로피를 한다고 함은, 원래 ground truth 로 나온 엔트로피에다 P 와 Q 사이의 엔트로피의 차이를 계산한다는 것이다.
즉 우리가 원하는 것은 output 으로 나온 Q 가 P 와 동일했으면 좋겠다는 것이다. (=좋은 네트워크이다)
따라서 학습을 한다는 것은 KL-Divergence 를 0으로 만들어주는 과정이다.

Degenerate Distribution : 하나만 1이고 나머지는 다 0 인 분포
