• NumPy
Python에서 대규모 다차원 배열을 다룰 수 있게 도와주는 라이브러리
→ 파이썬 리스트(List)에 비해, 빠른 연산을 지원하고 메모리를 효율적으로 사용
-기본적인 배열 만들기
list(range(10))
#[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
import numpy as np
np.array([1, 2, 3, 4, 5])
#array([1, 2, 3, 4, 5])
np.array([[1, 2], [3, 4]])
#array([[1, 2], [3, 4]])
np.array([1, 2, 3, 4], dtype='float’)
#array([1., 2., 3., 4.])-dtype / astype
배열 데이터의 타입을 알아보기 위해 dtype을 사용한다.
배열 데이터의 타입을 변환하기 위해 astype을 사용한다.
arr= np.array([1, 2, 3, 4], dtype=float)
arr #array([1., 2., 3., 4.])
arr.dtype #dtype(‘float64’)
arr.astype(int) #array([1, 2, 3, 4])
arr.dtype #dtype('int64')-다양한 배열 만들기
◦ np.zeros((Shape))
배열을 주어진 행렬만큼 0으로 채운다.
◦ np.ones((Shape))
배열을 주어진 행렬만큼 1로 채운다.
◦ np.arange(A,B,Step)
배열을 구간에서 주어진 간격만큼 떨어져있는 수들로 채운다.
◦ np.linspace(A,B,N)
배열을 구간 내 주어진 원소의 갯수만큼의 수들로 채운다.
np.zeros(10, dtype=int)
#array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
np.ones((3, 4), dtype=float)
#array([[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]])
np.arange(0, 20, 2)
#array([ 0, 2, 4, 6, 8, 10, 12, 14, 16, 18])
np.linspace(0, 1, 5)
#array([0. , 0.25, 0.5 , 0.75, 1. ])-난수로 채워진 배열 만들기
◦ np.random.random((Shape))
배열을 범위 내의 임의의 실수로 채운다.
◦ np.random.nomal(A,B,(Shape))
배열을 정규분포로부터 샘플링된 난수로 채운다.
◦ np.random.randint(A,B,(Shape))
배열을 범위 내의 임의의 정수로 채운다.
np.random.random((2, 2))
#array([[0.30986539, 0.85863508],[0.89151021, 0.19304196]])
np.random.normal(0, 1, (2, 2))
#array([[ 0.44050683, 0.04912487],[-1.67023947, -0.70982067]])
np.random.randint(0, 10, (2, 2))
#array([[3, 9],[3, 2]])-배열의 기초
x2 = np.random.randint(10, size=(3, 4))
# array([[2, 2, 9, 0],[4, 2, 1, 0],[1, 8, 7, 3]])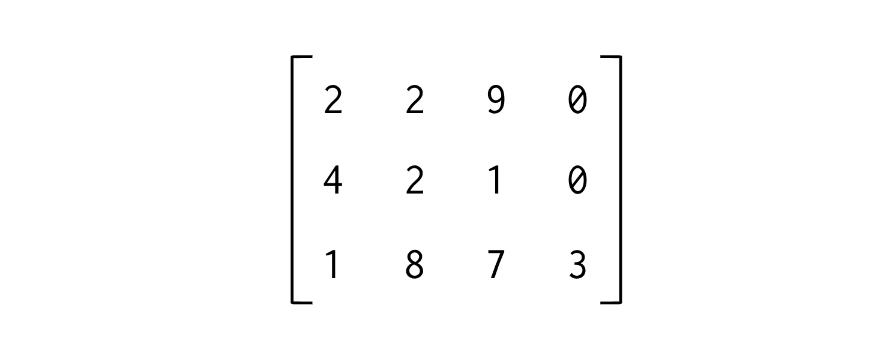
x2.ndim #2 → 배열의 차원 수
x2.shape #(3, 4) → 배열 각 차원(행,열..)의 크기
x2.size #12 → 전체 원소의 갯수 반환
x2.dtype #dtype(‘int64’) → 배열 데이터 타입• Indexing / Slicing
Indexing: 인덱스로 찾아냄

x = np.arange(7)
x[3] #3
x[7] #IndexError: index 7 is out of bounds
x[0]=10 #array([10, 1, 2, 3, 4, 5, 6])Slicing: 인덱스 값으로 배열의 부분을 가져옴

x = np.arange(7)
x[1:4] #array([1, 2, 3])
x[1:] #array([1, 2, 3, 4, 5, 6])
x[:4] #array([0, 1, 2, 3])
x[::2] #array([0, 2, 4, 6])• 배열의 모양 바꾸기
◦ reshape()
array의 shape를 변경
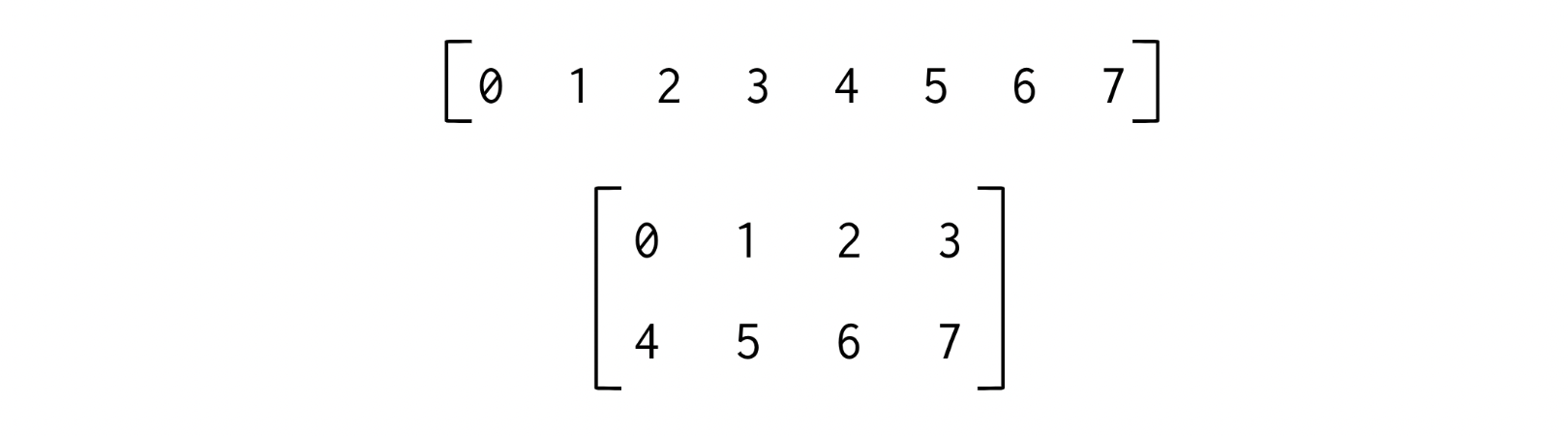
x = np.arange(8)
x.shape #(8,)
x2 = x.reshape((2, 4)) #array([[0, 1, 2, 3],[4, 5, 6, 7]])
x2.shape #(2, 4)◦ concatenate()
array를 이어 붙임
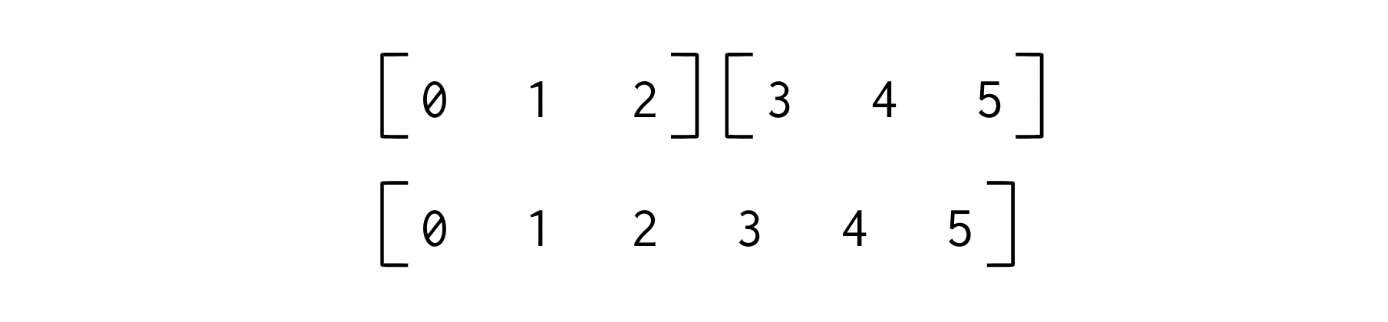
x = np.array([0, 1, 2])
y = np.array([3, 4, 5])
np.concatenate([x, y]) #array([0, 1, 2, 3, 4, 5])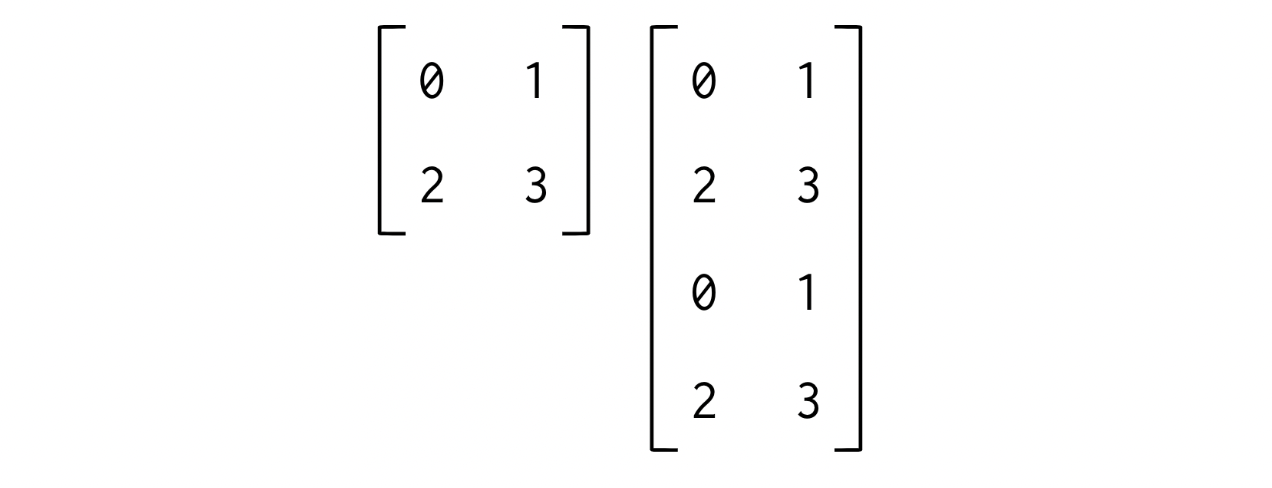
matrix = np.arange(4).reshape(2, 2)
np.concatenate([matrix, matrix], axis=0)◦ split()
axis 축을 기준으로 분할
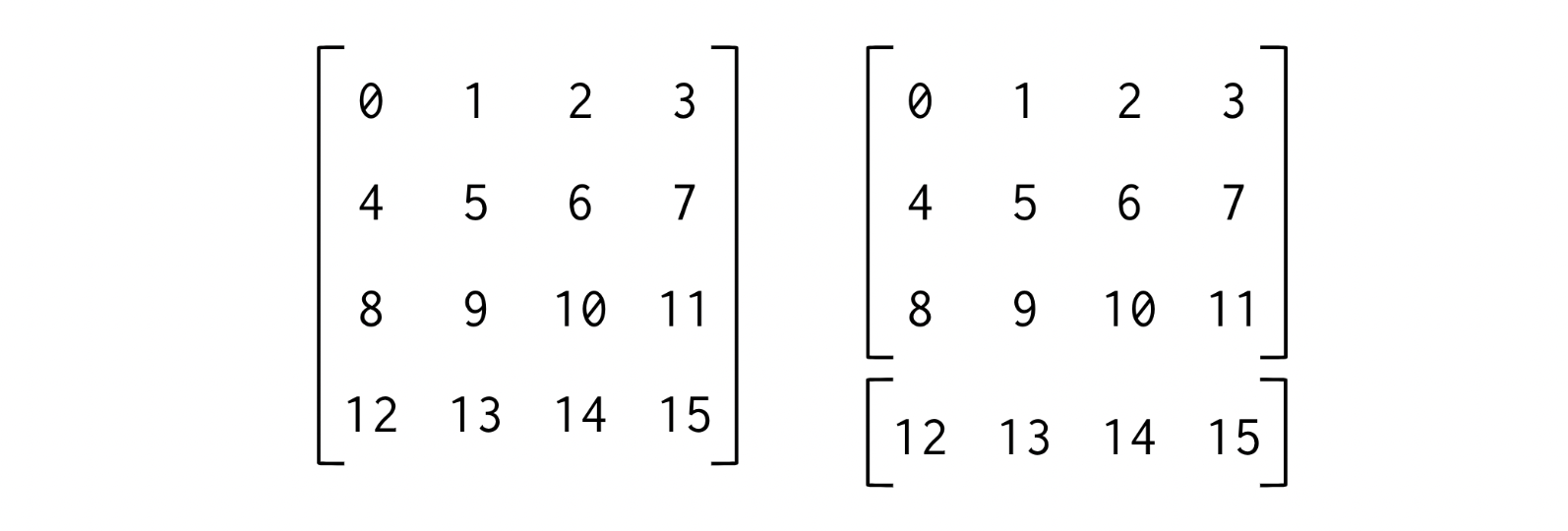
matrix = np.arange(16).reshape(4, 4)
upper, lower = np.split(matrix, [3], axis=0)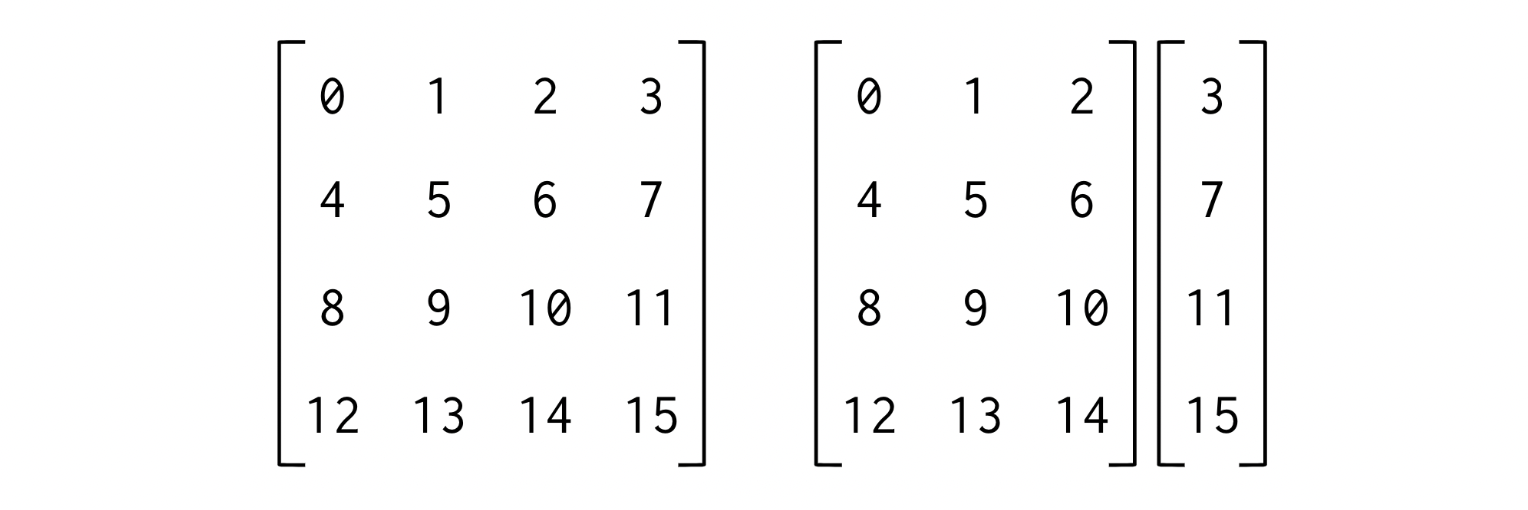
matrix = np.arange(16).reshape(4, 4)
left, right = np.split(matrix, [3], axis=1)• NumPy 연산
-사칙연산
array는 + - * / 에 대한 기본 연산을 지원
x = np.arange(4) #array([0, 1, 2, 3])
x + 5 #array([5, 6, 7, 8])
x - 5 #array([-5, -4, -3, -2])
x * 5 #array([ 0, 5, 10, 15])
x / 5 #array([0. , 0.2, 0.4, 0.6])-행렬 간 연산
다차원 행렬에서도 적용 가능
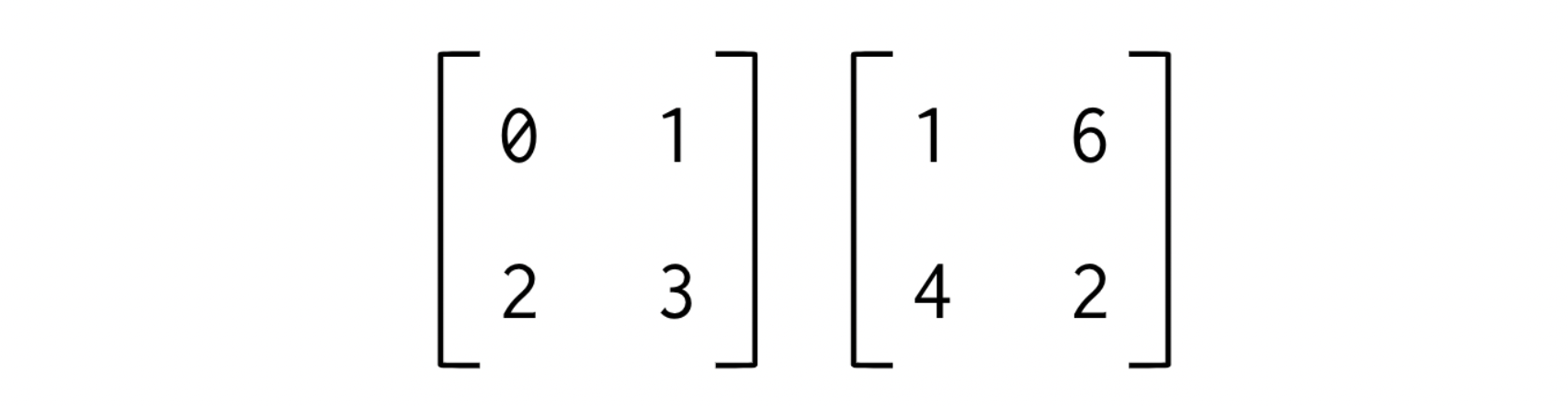
x = np.arange(4).reshape((2, 2))
y = np.random.randint(10, size=(2, 2))
x + y #array([[1, 7],[6, 5]])
x - y #array([[-1, -5],[-2, 1]])-브로드캐스팅
shape이 다른 array끼리 연산

matrix + 5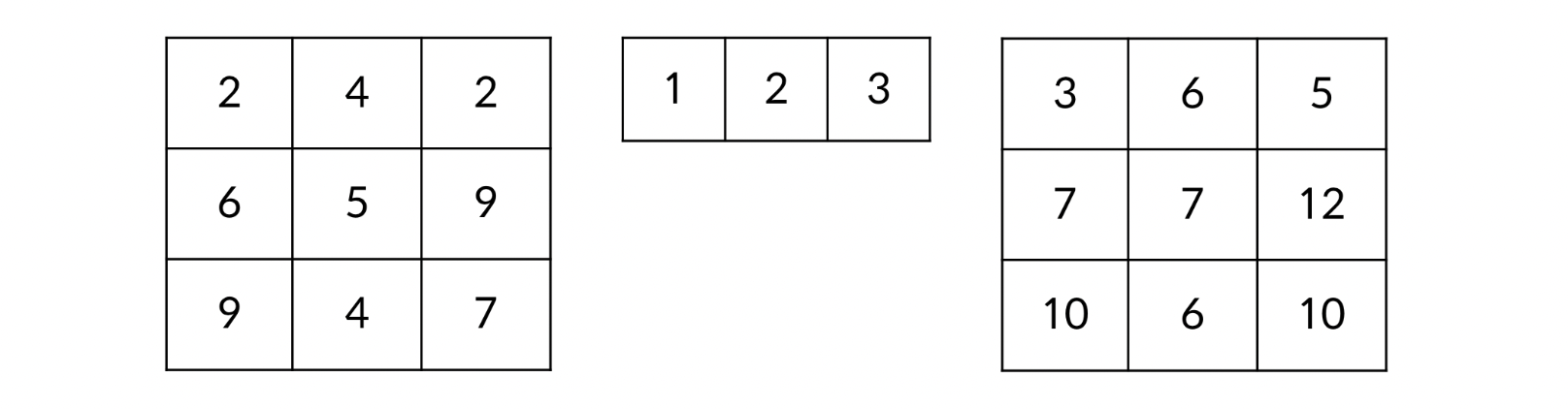
matrix + np.array([1, 2, 3])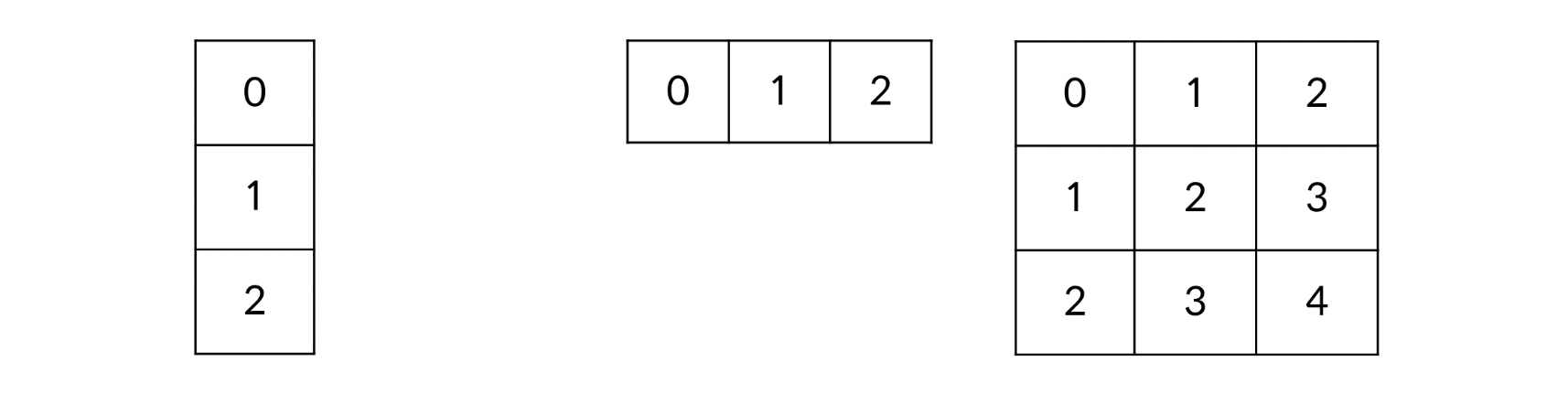
np.arange(3).reshape((3,1)) + np.arange(3)-집계함수
데이터에 대한 요약 통계
x = np.arange(8).reshape((2, 4))
np.sum(x) #28
np.min(x) #0
np.max(x) #7
np.mean(x) #3.5
np.sum(x, axis=0) #array([ 4, 6, 8, 10])
np.sum(x, axis=1) #array([ 6, 22])