네트워크의 유사도와 군집도
네트워크에서의 유사도 척도:Similarity Measures
그래프 내부의 인접한 두 정점 간의 유사도를 측정하려면?
-두 노드의 이웃이 얼마나 겹치는 지를 평가

유사도 척도의 정규화: Normalization
유사도 척도를 [0,1] 구간의 값으로 정규화 하는 방법
자카드 유사도:Jaccard Similarity
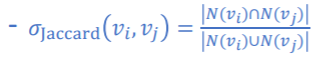
코사인 유사도:Cosine Similarity
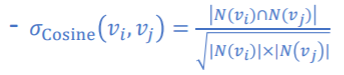
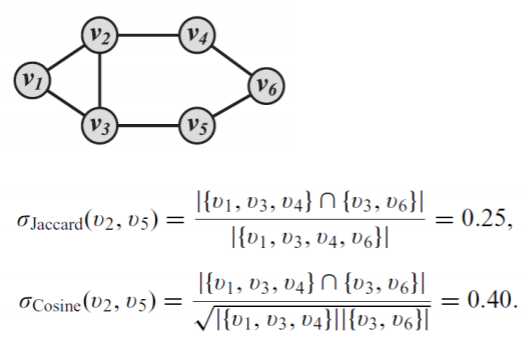
네트워크의 군집도:
전이적 연결: Transitive Linking
-유유상종: 내 친구의 친구는 내 친구일 가능성이 높다.
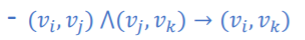
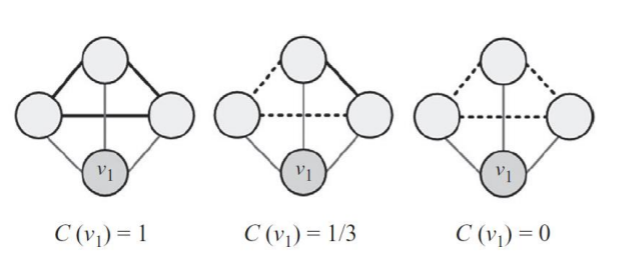
군집 계수: Clustering Coefficient
-노드들이 얼마나 서로 똘똘 뭉쳐 있는가를 평가
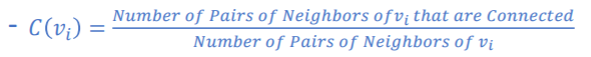
커뮤니티 분석: Community Analysis
군집 vs 커뮤니티: Cluster vs Community
-본질적으로는 같은 의미이나, 목적과 수단이 서로 다른 배경에서 출발
-군집: 특성에 의해 나누어진 군집을 발견하는 것이 목적 (IRIS)
-커뮤니티: 나누어진 군집을 발견해서 특성을 이해하는 것이 목적 (SNS)
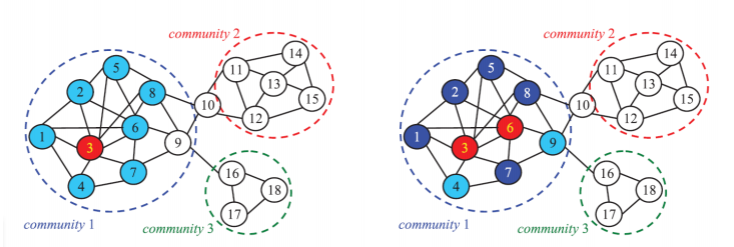
커뮤니티 발견:Community Detection
-네트워크의 연결 구조를 이용한 클러스터링 알고리즘
-때로는 고정된 커뮤니티가 아닌, 진화하는 커뮤니티 발견이 문제일 수 있음
Community Detection Algorithms:
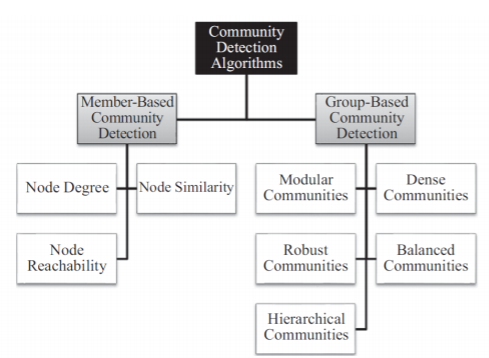
member based community detection->Node Similarity-> 유사도 거리-> k-means
group-based community detection->Hierarchical Communities
커뮤니티 발견 알고리즘
커뮤니티 구조의 평가:
지도 학습:
-실제로 해당 노드가 어떤 커뮤니티에 속하는 지를 아는 경우
-혼동 행렬을 통한 평가 지표를 사용할 수 있음
비지도 학습:
-해당 노드가 어떤 커뮤니티에 속하는 지를 모르는 경우
-커뮤니티의 구조가 네트워크의 구조를 얼마나 잘 반영했는가를 평가
모듈성:Modularity
기본 아이디어: 커뮤니티 구조는 랜덤 네트워크의 구조와는 달라야 한다.
가중치 없는 무방향 그래프 G=(V,E) 에서,

뉴먼 모듈성 지수: Newman's Modularity

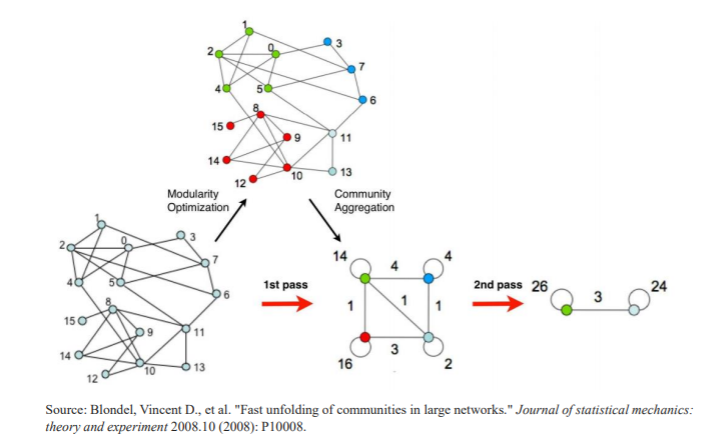
루베인 알고리즘: Louvain Method
뉴먼의 모듈성 지수를 최적화하는 알고리즘
1단계: 한 노드를 현재 커뮤니티에서 빼내어 인접한 커뮤니티에 재배치
-모듈성 지수가 증가하면 해당 커뮤니티에 배치, 아니면 원래 커뮤니티에 둠
2단계: 1단계에서 생성된 커뮤니티를 하나의 노드로 하는 그래프를 새로 만듬
-커뮤니티의 내부 링크는 self-loop의 가중치로,
-커뮤니티 간 연결은 해당 커뮤니티 간의 연결 가중치의 합으로 결정
위와 같은 pass(1단계+2단계)를 모듈성 지수 증가가 없을 때까지 반복
->simple graph 생성 아님!
라벨 전파 알고리즘 : LPA, Label Propagation Algorithm
가정: 내가 속한 커뮤니티는 내 이웃들이 많이 속해 있는 커뮤니티와 같다.
각자가 가진 라벨을 네트워크에 전파하여 마지막에 남은 라벨로 커뮤니티 결정.
LABEL-PROPAGATION-ALGORITHM:
-모든 노드가 각자의 고유한 라벨을 소유함
-임의의 순서로 각 노드는 이웃 노드들이 가장 많이 가진 라벨로 업데이트 함
-모든 노드의 라벨이 이웃 노드들 중 가장 많은 라벨로 구성되면 종료함
-이웃 노드의 라벨의 개수가 동일하면 임의로 하나 선정함
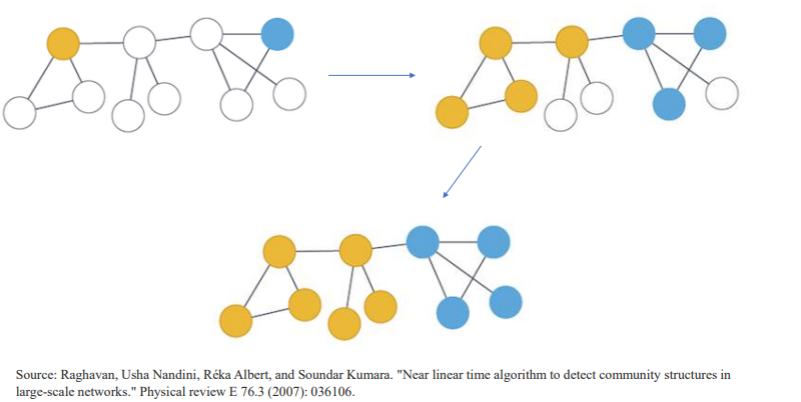
Louvain과 마찬가지로 modularity 최적화 과정,non deterministic 알고리즘 but 실행 속도가 빨라서 여러번 실행 후에 가장 모듈성 지수가 높은 결과를 선택할 수 있ㄸ.
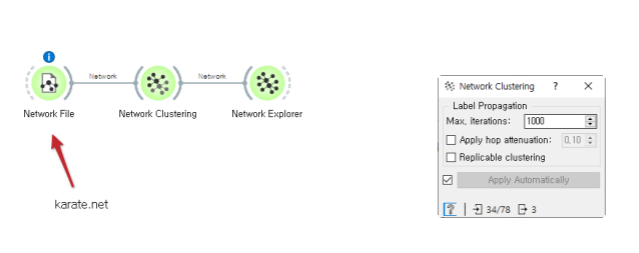
오렌지:Network Clustering
네트워크의 동역학 분석
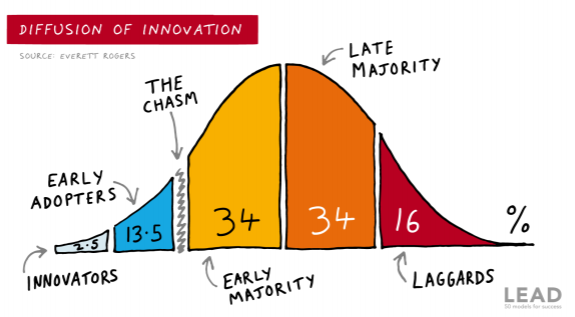
개혁의 확산: Diffusion of Innovation
에버렛 로저스: 사람들이 신기술을 받아들이는 데에는 일정한 패턴이 있다.
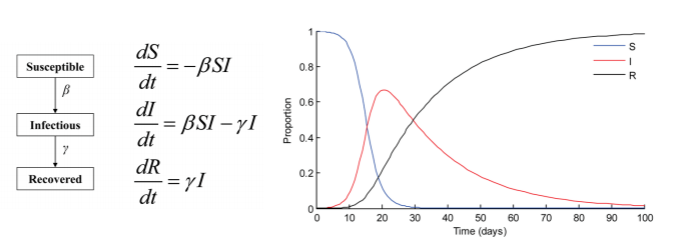
질병의 확산 모델: The Spread of Disease, Epidemics
SIR 모델: 전염병의 확산을 분석하는 가장 기본적인 모델
-Susceptible: 감염될 수 있는 개체
-Infected: 감연된 개체
-Recovered: 면역된 개체
정보의 캐스케이드: Information Cascade
101마리 원숭이 현상: 다수의 사람들이 동시에 같은 결정을 내리게 되는 현상
소문의 확산, 가짜 뉴스의 확산 등을 모델링할 때
ICM:Independent Cascade Model
-정보의 확산을 독립된 개체의 확률적 결정으로 판단
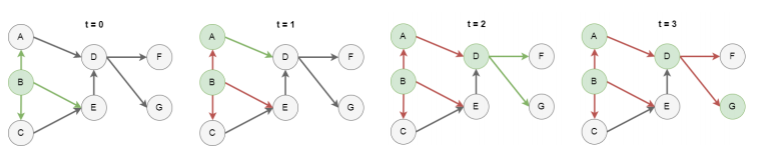
영향력 극대화 문제: Influence Maximization Problem
소셜 네트워크에서 영향력을 극대화할 수 있는 사람들의 집합을 찾는 문제
k가 주어졌을 때, 가장 확산 범위가 높은 k개의 노드 선택하기
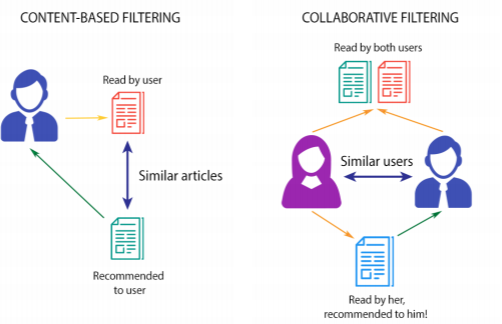
추천 알고리즘: Recommendation Algorithms
사용자가 선호할 아이템을 예측하여 해당 항목을 추천하는 알고리즘
콘텐츠 기반 추천: Content- based Recommendations
-아이템이 사용자의 성향에 잘 맞는가를 판단함 (사용자-아이템 유사도)
협업 필터링: Collaborative Filtering
-유사한 사용자들이 선호하는 아이템을 추천 (사용자-아이템 행렬)
추천 시스템을 위한 네트워크 모델
이분할 그래프:Bipartite Network
삼분할 그래프:Tripartite Network
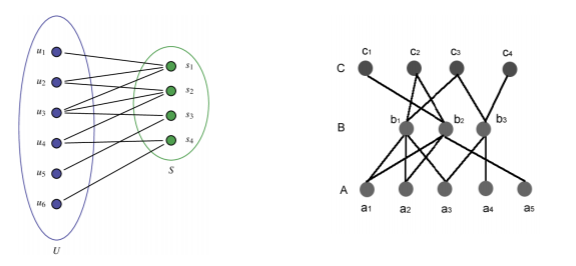
이분그래프
삼분할그래프
