ARIMA model (ARIMA, SARIMA, SARIMAX)

ARIMA 모델

ARIMA 모델은 Autoregressive Integrated Moving Average의 약자이며, 과거 관측값과 예측 오차를 기반으로 미래 값을 예측하는 통계적 시계열 분석 모델이다.

ARIMA 모델은 아래와 같은 세 요소로 구성된다.

• AR (자기회귀, Autoregressive)
  과거 값(시차 값)들의 가중합으로 현재 값을 설명
• I (차분, Integrated)
  비정상 시계열을 정상 시계열로 만들기 위한 차분 횟수
• MA (이동 평균, Moving Average)
  과거의 예측 오차들의 가중합으로 현재 값을 설명

ARIMA(p, d, q) 모델의 파라미터

• p: AR(자기회귀) 차수
• d: I(차분) 차수
• q: MA(이동 평균) 차수

ARIMA 모델 수식

여기서:
• $B$는 백쉬프트 연산자 (예: $By_t = y_{t-1}$)
• $\phi(B): AR(p)$ 다항식
• $\theta(B): MA(q)$ 다항식
• $d:$ 차분 횟수
• $\varepsilon_t:$ white noise (예측 오차)

사용 전제

•	시계열 데이터여야 함
•	정상성(stationarity): 
		평균과 분산이 시간에 따라 변하지 않아야 함 → 이를 위해 차분(d) 수행

적용 순서

1.	데이터 시각화 및 정상성 여부 확인 (ADF Test 등)
2.	정상성이 없으면 차분(d) 수행
3.	ACF/PACF 분석을 통해 p, q 결정
4.	ARIMA(p, d, q) 모델 학습
5.	예측 및 성능 평가 (RMSE, AIC 등)

장점

시계열 예측에 매우 강력
간단하고 해석 가능함
짧은 데이터로도 동작 가능

단점

비정상 시계열일 경우 전처리 필요
외부 변수 반영 불가 (→ SARIMAX, VAR 필요)
복잡한 비선형 패턴에는 한계

---

SARIMA 모델

이 ARIMA 모델에서 계절성(Seasonal)을 포함하면 SARIMA(Seasonal ARIMA)모델이 된다.

SARIMA 모델 수식

$\Phi_P(B^s) \, \phi_p(B) \, (1 - B)^d \, (1 - B^s)^D \, y_t = \Theta_Q(B^s) \, \theta_q(B) \, \varepsilon_t$

여기서:

• $B$ : 백쉬프트 연산자 (예: $B y_t = y_{t-1}$)
• $\phi_p(B)$ : 비계절 AR (자기회귀) 다항식, 차수 $p$
• $\Phi_P(B^s)$ : 계절 AR (자기회귀) 다항식, 계절 차수 $P$, 주기 $s$
• $(1 - B)^d$ : 비계절 차분 연산, 차수 $d$
• $(1 - B^s)^D$ : 계절 차분 연산, 계절 차수 $D$, 주기 $s$
• $\theta_q(B)$ : 비계절 MA (이동 평균) 다항식, 차수 $q$
• $\Theta_Q(B^s)$ : 계절 MA (이동 평균) 다항식, 계절 차수 $Q$, 주기 s
• $\varepsilon_t$ : 백색 잡음 (white noise), 예측 오차 항

SARIMA 모델은 계절성을 가진 시계열 데이터의 과거 패턴을 기반으로 미래 값을 예측하는 통계 모델이다.

---

SARIMAX 모델

SARIMA 모델에서 한번 더 나아가 외생 변수까지 포함하는 모델인 SARIMAX (SARIMA + eXogenous variables) 모델이다.과거 데이터의 패턴뿐만 아니라 추가적인 외생 변수까지 고려한다.

SARIMAX 모델 수식

$\Phi_P(B^s) \, \phi_p(B) \, (1 - B)^d \, (1 - B^s)^D \, y_t = \beta X_t + \Theta_Q(B^s) \, \theta_q(B) \, \varepsilon_t$

여기서:
• $\Phi_P(B^s)$ : 계절 자기회귀(Seasonal AR) 다항식, 차수 $P$, 주기 $s$
• $\phi_p(B)$ : 비계절 자기회귀(AR) 다항식, 차수 $p$
• $(1 - B)^d$ : 비계절 차분 연산, 차수 $d$
• $(1 - B^s)^D$ : 계절 차분 연산, 차수 $D$, 주기 $s$
• $y_t$ : 예측 대상 시계열 값 (예: 매출, 방문자 수 등)
• $\beta X_t$ : 외생 변수의 선형 조합 (외부 요인 $X_t$에 대한 영향)
• $\Theta_Q(B^s)$ : 계절 이동 평균(Seasonal MA) 다항식, 차수 $Q$, 주기 $s$
• $\theta_q(B)$ : 비계절 이동 평균(MA) 다항식, 차수 $q$
• $\varepsilon_t$ : white noise (백색 잡음), 평균 0의 오차 항

SARIMAX 모델은 자기회귀, 차분, 이동평균, 계절성 요인에 더해 외부 변수의 영향까지 반영하여 시계열 데이터를 정밀하게 예측하는 통계 모델이다.

---

데이터 전처리

ARIMA 게열의 모델은 정상성(Stationary)을 가진 시계열 모델만을 다룰 수 있다.

Stationary의 조건

1.	평균이 일정하다 (constant mean)
→ 시간에 따라 값의 중심이 움직이지 않아야 한다
(예: 꾸준히 100 근처에서 왔다갔다)

2.	분산이 일정하다 (constant variance)
→ 변동폭이 일정해야 함
(예: 시간대별로 들쭉날쭉 차이가 심해지면 안 된다)

3.	자기공분산이 일정하다 (constant autocovariance)
→ 시차(lag)가 같으면 어느 시점이든 상관 구조가 같아야 한다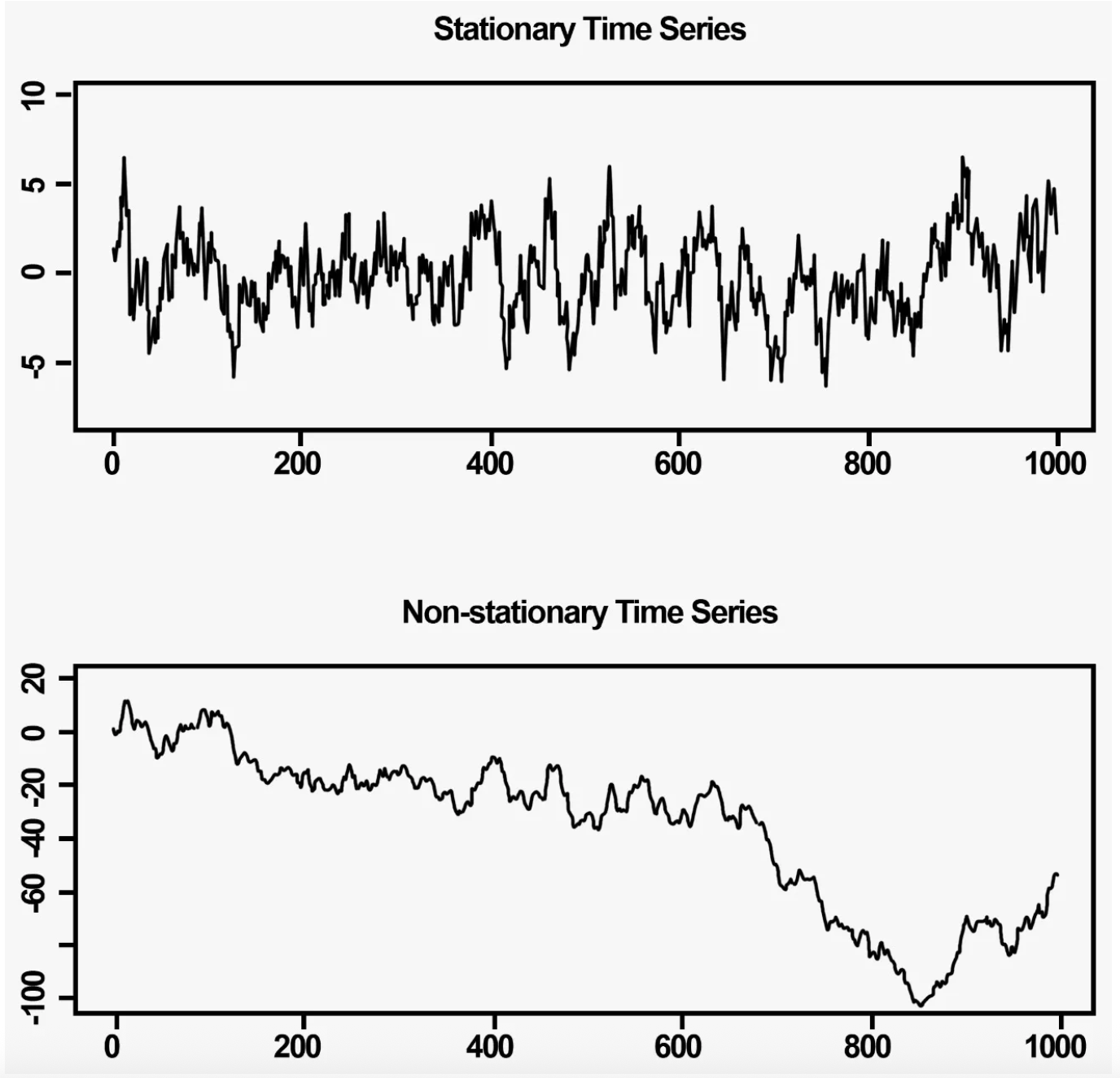

Stationary Testing Methods

1. Augmented Dickey–Fuller (ADF) Test
   • 귀무가설(H₀): 시계열에 단위근(unit root)이 존재 → 비정상(non‑stationary)
   • 대립가설(H₁): 정상성 또는 추세 정상성(trend‑stationary)
   • 테스트 통계량이 임계값보다 작거나(더 음수일수록), p-value < 통상 0.05 → 비정상 가설 기각 → 정상성 유의
   • 시계열 잔차에 포함된 지연항(lags)을 통해 자기상관을 조정 가능

2. KPSS (Kwiatkowski‑Phillips‑Schmidt‑Shin) Test
   • 귀무가설(H₀): 시계열은 정상 또는 추세 수준에서 정상성 있음 (trend‑stationarity)
   • 대립가설(H₁): 비정상 또는 단위근 존재
   • 테스트 통계량이 임계값보다 크거나, p-value < 0.05 → 정상성 가설 기각 → 비정상 판정
   • ADF와 반대 방향의 가설 구조로 서로 보완적 판단 가능

두 테스트 함께 사용 권장
• ADF가 정상성 판단, KPSS가 비정상 판단 → 경계 케이스 가능 → 추가 분석 필요

사례:
• ADF: 정상성 → KPSS: 비정상성 → 추가 차분 또는 경향 제거 검토
• ADF: 비정상성 → KPSS: 정상 → 데이터 near-stationary 가능성 → 시계열 그래프, ACF 등으로 재확인 필요

3. ACF (Autocorrelation Function) 분석
   • 시계열의 정상성 검사 및 자기상관 구조 분석을 위한 ACF(Autocorrelation Function) 플롯 분석

방법	귀무가설 (H₀)	해석 기준	정상성 시그널
ADF 테스트	단위근 존재 → 비정상 시계열	p‑value ≤ 0.05 ⇒ H₀ 기각 ⇒ 정상성 있음	테스트 통계량이 기준값보다 더 음수임
KPSS 테스트	정상성 존재 (trend‑stationary)	p‑value > 0.05 ⇒ H₀ 유지 ⇒ 정상성 있음	통계량이 임계값 이하, p‑value 비교적 큼
ACF 분석	— (그래프 기반 시각적 분석)	ACF가 lag 증가 시 빠르게 0으로 수렴	빠른 감쇠 또는 lag 이후 유의미한 spike 없음

데이터 전처리

비정상으로 판단되는 경우	처리 방법	설명 및 주의 사항
추세(Trend) 존재	1차 차분(differencing)	(yt - y{t-1}) 형태로 추세 제거 → 평균 안정화
계절성(Seasonality) 존재	계절 차분(seasonal differencing)	예: 월별 데이터이면 (yt - y{t-12}) → 주기 패턴 제거
추세 + 계절성 동시에 존재	혼합 차분: 1차 + 계절 차분 적용	예: ( \nabla ( \nabla_{s} y_t ) ) 형태. 순서 조정 주의
비선형 추세 또는 분산 불안정	로그 변환, 제곱근 변환 (variance stabilization)	분산이 커지는 패턴 있을 때 효과적
추세 구조 추정 가능	detrending (회귀로 추세 제거)	선형 회귀로 (Y_t = a t + b + e_t), residual을 안정화 시점 분석
여전히 정상성 부족	추가 차분 반복	필요하면 2차, 3차 차분 적용. I(d)를 늘려 정상성 확보
대안적 접근	상태공간 모델, 비정상 모델 (Non-stationary 모델링)	ARIMA 기반이 어려우면 상태공간 모델 등 비정상성 자체를 모델링

Prediction 후 Evaluation

📊 예측 성능 지표 해석 기준표

지표 이름	계산 방식	의미	해석 기준 예시
MAE (Mean Absolute Error)	평균 절대 오차	예측값과 실제값 차이의 절댓값 평균	작을수록 좋음. 단위는 예측 대상과 동일
MSE (Mean Squared Error)	평균 제곱 오차	오차를 제곱한 후 평균 → 큰 오차에 더 민감	값이 클수록 나쁨. 단위는 제곱된 값
RMSE (Root Mean Squared Error)	MSE의 제곱근	MSE를 원래 단위로 되돌린 지표	MAE보다 큰 오차에 민감. 작을수록 좋음
MAPE (Mean Absolute Percentage Error)	평균 상대 오차 비율 (%)	예측 오차를 실제값 기준으로 비율화한 값	10% 이하 → 매우 양호, 20% 이하 → 괜찮음