예측모델 실습1 (SARIMA)

SARIMA 모델 실습을 위해 kaggle에서 Data Model - Pizza Sales 을 다운 받았다.

이 데이터셋은 2015년 1년간의 피자 판매 데이터이다.
이 데이터를 전처리하고 SARIMA 모델을 적용해 매출 예측을 진행해볼 예정이다. (실습 환경: Google Colab)
(참고영상: https://www.youtube.com/watch?v=ySiKZwoTX54&t=317s)

day 기준 전체 매출 예측을 해보려고 한다.

데이터 전처리

데이터셋을 살펴보니

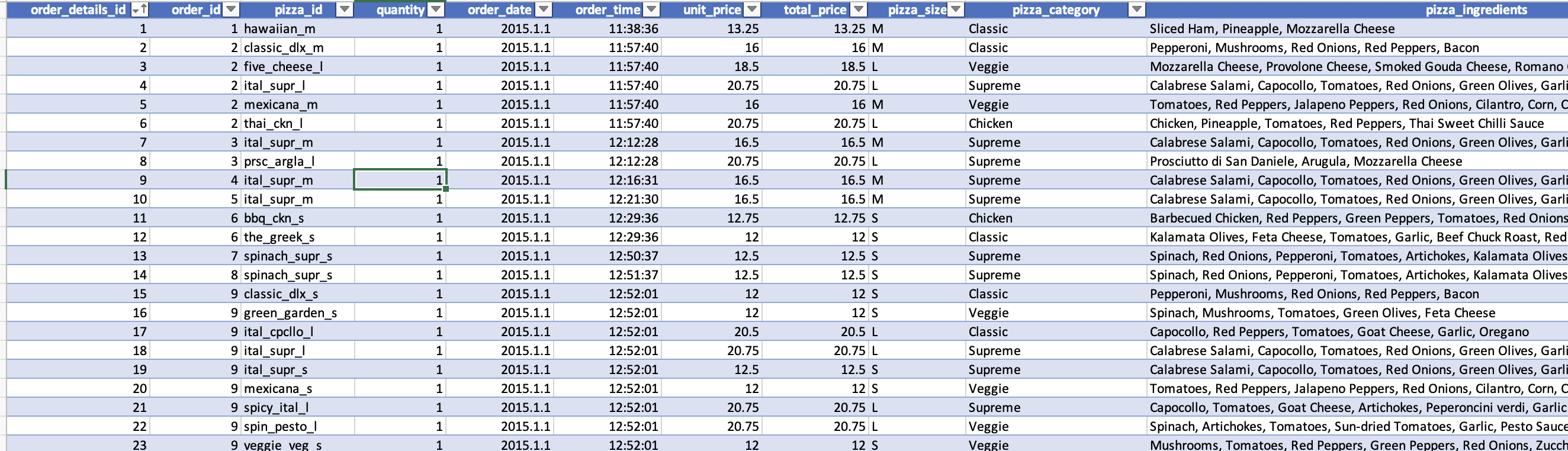
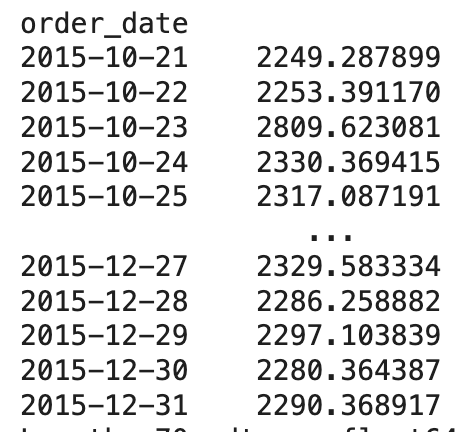
이런 식으로 pizza_id, quantity, order_date, order_time, unit_price, total_price 등 여러 종류의 데이터들이 있다.
내가 필요한 데이터는 day 기준 매출의 총 합이다.

그래서 일단 order_date와 total_price만 남기고 모든 column을 삭제했다.

이후 같은 일자의 total_price를 모두 합쳐야 한다.

import pandas as pd

try:
    df = pd.read_csv('date&price.csv')

    # Convert 'order_date' to datetime objects if it's not already
    df['order_date'] = pd.to_datetime(df['order_date'])

    # Group by 'order_date' and sum 'total_price'
    grouped_df = df.groupby('order_date')['total_price'].sum().reset_index()

    # Save the result to a new CSV file
    grouped_df.to_csv('aggregated_orders.csv', index=False)

    print("Aggregation complete. The result is saved to 'aggregated_orders.csv'")

except FileNotFoundError:
    print("Error: File not found. Please check the file path.")
except KeyError as e:
    print(f"Error: Column '{e}' not found in the CSV file. Please ensure 'order_date' and 'total_price' columns exist.")
except Exception as e:
    print(f"An unexpected error occurred: {e}")

이러한 코드로 같은 일자의 매출을 합쳤다. 결과는 아래와 같다.

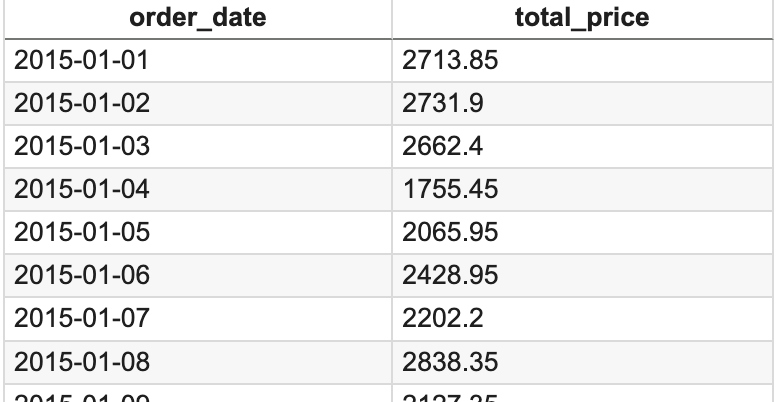
이 데이터를 그래프로 보면 아래와 같다.

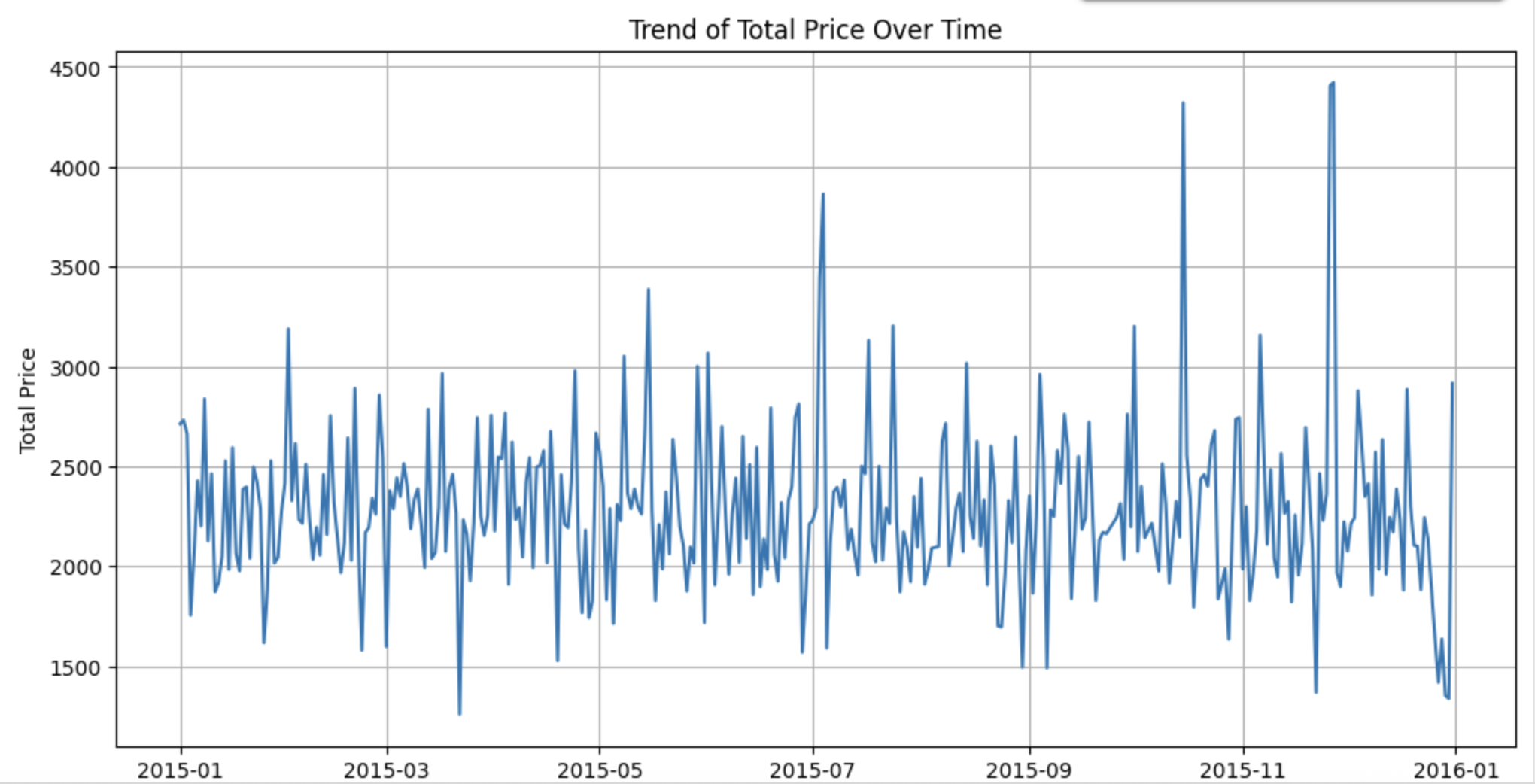
눈으로만 보면 stationary 인지 잘 모르겠다.
그래서 테스트를 해보았다.

Data Stationary Test

ADF 테스트를 진행했다.

# 필요한 라이브러리 설치
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
import pandas as pd # Import pandas here as well

# CSV 불러오기 (직접 파일 경로 지정)
try:
    df = pd.read_csv("aggregated_orders.csv", parse_dates=["order_date"])
    df.set_index("order_date", inplace=True)
    ts = df["total_price"]

    # 시계열 시각화
    ts.plot(figsize=(10, 4), title="일별 총 주문 금액")
    plt.grid()
    plt.show()

    # ADF 테스트 함수 정의
    def adf_test(series):
        print(">> ADF Test 결과")
        result = adfuller(series, autolag='AIC')
        labels = ['ADF Statistic', 'p-value', '#Lags Used', 'Number of Observations Used']
        for value, label in zip(result[:4], labels):
            print(f"{label}: {value:.4f}")
        print("Critical Values:")
        for key, value in result[4].items():
            print(f"   {key}: {value:.4f}")
        if result[1] <= 0.05:
            print("정상성 있음 (p <= 0.05)")
        else:
            print("비정상 시계열 (p > 0.05) → 차분 필요")

    # ADF 테스트 실행
    adf_test(ts)

except FileNotFoundError:
    print("Error: 'aggregated_orders.csv' not found. Please ensure the file exists in the correct directory.")
except KeyError as e:
    print(f"Error: Column '{e}' not found in the CSV file. Please ensure 'order_date' and 'total_price' columns exist.")
except Exception as e:
    print(f"An unexpected error occurred: {e}")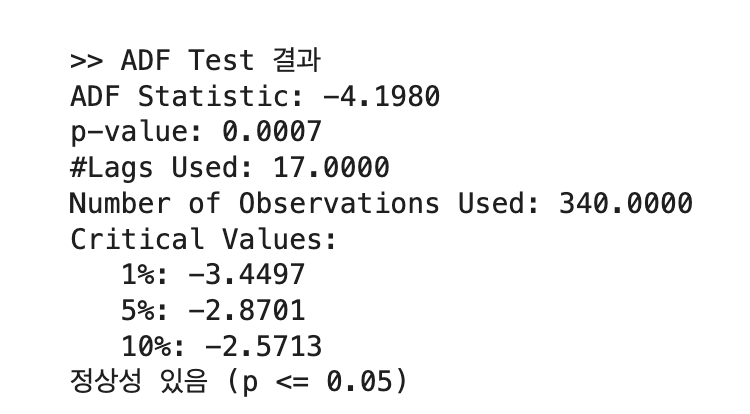

테스트 p-value가 0.0007로 0.05보다 적어 귀무가설이 기각되며 정상성이 있다는 결과가 나왔다. 그러므로 바로 SARIMA 모델의 적용이 가능하다.

!pip install pmdarima
from pmdarima import auto_arima

을 실행했는데 계속 auto_arima impor가 안돼서 검색을 통해 해결 코드를 찾았다.

# Install Condacolab to integrate Conda with Colab
!pip install -q condacolab

# Import and run Condacolab to enable Conda
import condacolab
condacolab.install()

# Install pmdarima from conda-forge using Conda
!conda install -c conda-forge pmdarima -y

위에 코드를 실행 후. 다시 import를 하니 잘 되었다.

day 기준 데이터이므로 asfreq("D")로 CSV 파일 불러오기

df = pd.read_csv("aggregated_orders.csv",
            index_col = "order_date",
            parse_dates = True).asfreq("D")

결측치 제거

training_y = df.iloc[:-73]["total_price"].dropna()
test_y = df.iloc[-73:]["total_price"].dropna()

전체가 1냔(365일) 이므로 그거에 약 20%인 73일의 데이터를 뺀 나머지를 테스팅, 73일의 데이터를 트레이닝 셋에 넣었다.

SARIMA model

model = auto_arima(y=training_y, m=7, seasonal=True, trace=True)

auto_arima 함수 호출
계절성을 고려하므로 seasonal은 True로 설정,
그리고 day 기준이므로 m=7을 사용한다고 영상에서 설명해주었다.
(trace는 진행상태 출력하게하는 입력값)

Prediction

forecast_horizon = len(test_y)

predictions = pd.Series(model.predict(n_periods=forecast_horizon))  # 예측 개수는 test_y 크기만큼
predictions.index = test_y.index
print(predictions)

Prediction 값 출력
n_periods의 값이 test_y (테스팅 데이터셋)의 개수와 일치해야한다.
위에서 결측치를 제거하면서 미리 설정한 73개가 아닐수 있으므로 len(test_y)로 개수를 확인후 그만큼만 n_periods에 입력하게 하였다.

Prediction results

Visualization

training_y['2015-10-21':].plot(figsize = (16, 6), legend = True)
test_y.plot(legend = True)
predictions.plot(legend = True)

Prediction 값이 2015-10-21 부터 존재하므로 이때부터만 그래프로 그리게 설정
testing data set으로 빼둔 값과 Prediction 값을 비교

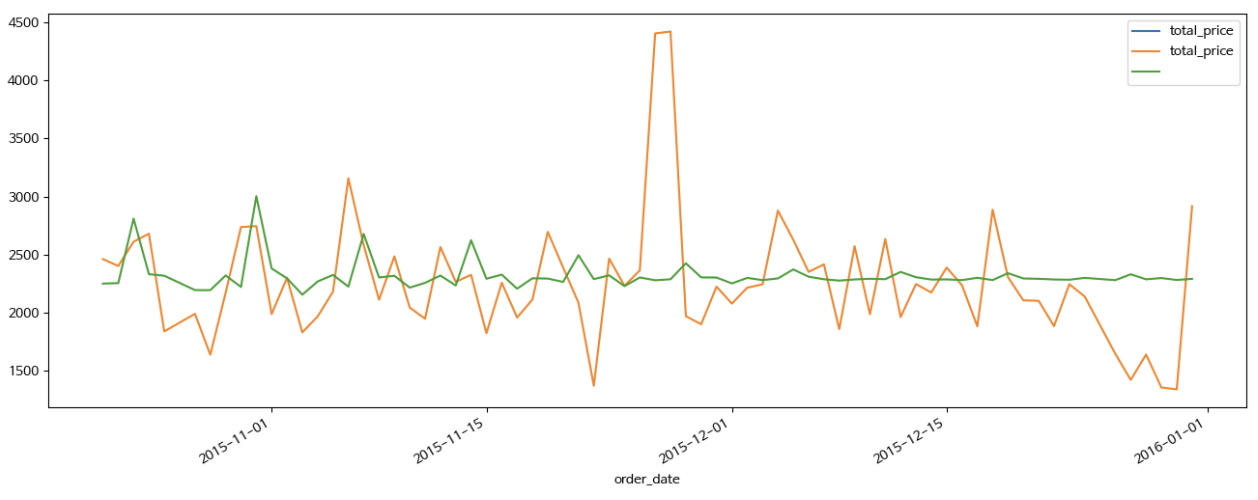
생각보다 너무 다르다..

Evaluation

일단 수치적으로 이 예측을 평가해보자

평가할 지표는 다음과 같다

지표 이름	계산 방식	의미	해석 기준 예시
MAE (Mean Absolute Error)	평균 절대 오차	예측값과 실제값 차이의 절댓값 평균	작을수록 좋음. 단위는 예측 대상과 동일
MSE (Mean Squared Error)	평균 제곱 오차	오차를 제곱한 후 평균 → 큰 오차에 더 민감	값이 클수록 나쁨. 단위는 제곱된 값
RMSE (Root Mean Squared Error)	MSE의 제곱근	MSE를 원래 단위로 되돌린 지표	MAE보다 큰 오차에 민감. 작을수록 좋음
MAPE (Mean Absolute Percentage Error)	평균 상대 오차 비율 (%)	예측 오차를 실제값 기준으로 비율화한 값	10% 이하 → 매우 양호, 20% 이하 → 괜찮음

from sklearn.metrics import mean_absolute_error, mean_squared_error
import numpy as np

# MAE
mae = mean_absolute_error(test_y, predictions)

# MSE & RMSE
mse = mean_squared_error(test_y, predictions)
rmse = np.sqrt(mse)

# MAPE
mape = np.mean(np.abs((test_y - predictions) / test_y)) * 100

# 출력
print(f"MAE: {mae:.2f}")
print(f"MSE: {mse:.2f}")
print(f"RMSE: {rmse:.2f}")
print(f"MAPE: {mape:.2f}%")

위 코드로 평가했을때

MAE: 357.71
MSE: 278674.34
RMSE: 527.90
MAPE: 16.47%

아래와 같은 수치가 나왔다.

일단 MAPE는 16.47%로 20%는 넘지않아 나쁘지는 않은 결과가 나왔다.
하지만 RMSE가 꽤 높다. 11월 말에 갑자기 튀는 데이터를 예측하지 못해 이런 결과가 나온것 같다.

R2 점수도 확인해 보았다.

from sklearn.metrics import r2_score

r2 = r2_score(test_y, predictions)

print(f"R² Score: {r2:.4f}")

좀 충격적인 결과가 나왔다.
R² Score: -0.0035
R2 점수가 마이너스인 모델은 처음봤다...

R² Score 범위	해석
0.9 ~ 1.0	매우 우수한 예측 (Excellent)
0.7 ~ 0.9	좋은 예측 (Good)
0.5 ~ 0.7	괜찮은 예측 (Fair)
0.3 ~ 0.5	낮은 예측력 (Low)
0.1 ~ 0.3	매우 낮은 예측력 (Very Low)
0 ~ 0.1	거의 설명 못함 (Barely useful)
< 0	모델이 평균보다도 못함 (Poor Model)

찾아보니 그냥 평균값으로 예측한 결과보다 더 예측을 못하면 마이너스가 나온다고 한다.

수정 1

주기(m)을 30으로 바꾼후 다시 테스트 해보기로 했다.

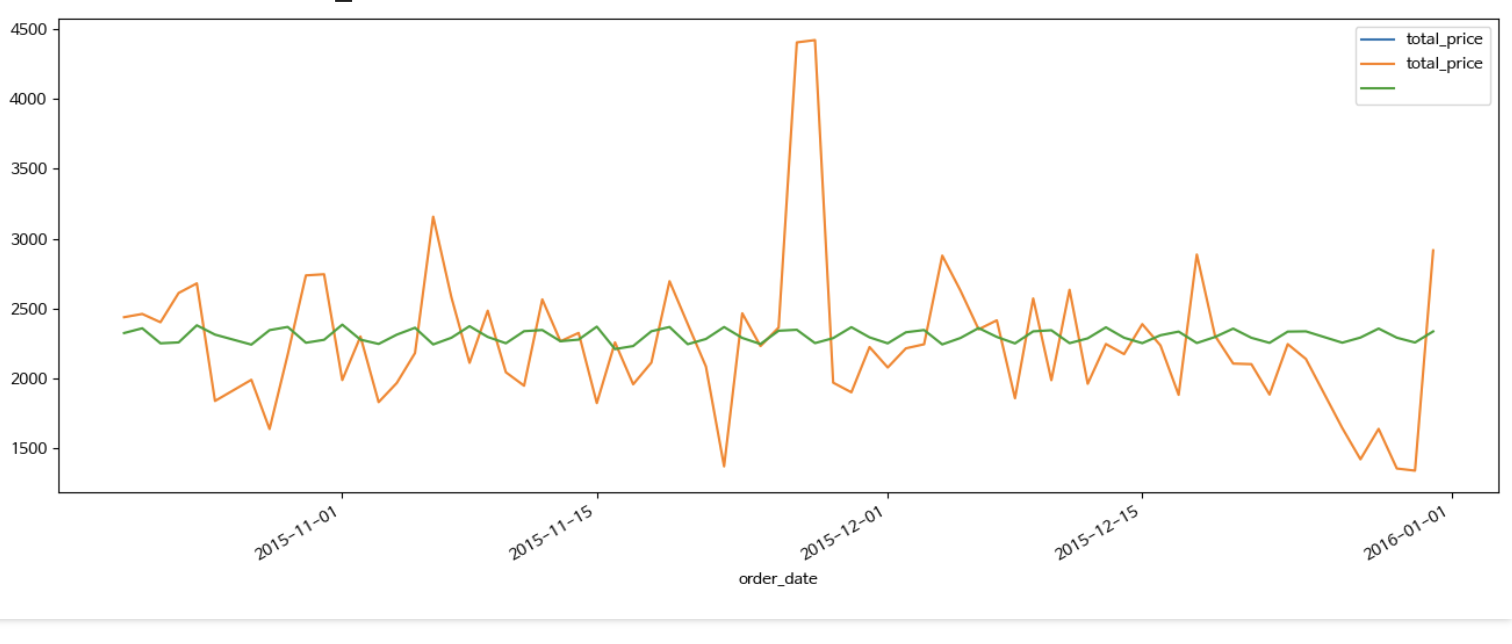
model = auto_arima(y=training_y, m=30, seasonal=True, trace=True)

이렇게만 수정후 다시 테스트를 해보았다.

이렇게 하니 예측값이 거의 직선에 가깝게, 평균과 크게 다르지 않게 나왔다.

수정 2

생각을 해보니 결측치를 제거하면 요일 순서가 틀어져 m=7로 계절성을 고려하며 예측했을때 오류가 생길수 있다고 생각해 결측치를 제거한 후 그 자리에 새 정보를 채우는 코드를 추가해야 한다.

아래의 코드로 그 작업을 진행하였다.

df["total_price"] = df["total_price"].interpolate(method="linear")
 # 결측치 보간 후 test, train dataset 분할
training_y = df.iloc[:-73]["total_price"]
test_y = df.iloc[-73:]["total_price"]

이후 다시 m=7로 설정하고 테스트를 해봤다.

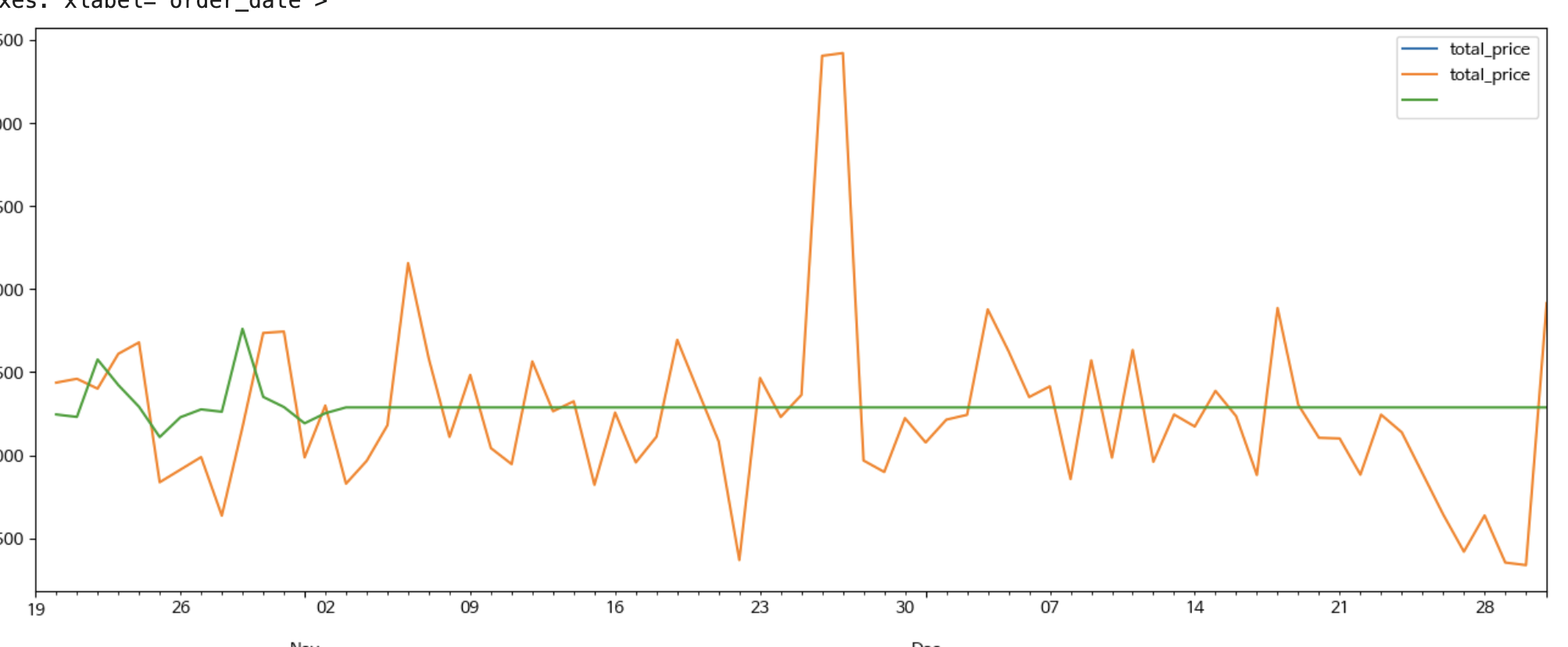
이렇게 하니 11월 예측치부터 예측값이 모두 평균값으로 나온다.

수정 3

SARIMA 모델에서 장기 예측으로 갈수록 값이 평균에 수렴하는 문제가 자주 발생한다고 한다.

이 문제를 해결해보고자 일단 결측치 보간 방식을 주기성을 보존하도록 바꿨다.

df["total_price"] = df["total_price"].interpolate(method="time")

그래도 똑같다..

단기를 예측해도 R2가 계속 마이너스가 나온다..
더 많은 데이터를 찾아서 SARIMAX나 LSTM을 시도해 봐야겠다.

회고

Problem
사용한 데이터가 1년짜리인데 10월까지 학습시키고 11,12월에 테스트를 하다보니 연 단위의 예측이 약간 안되는것 같다. 또한 요일이나 공휴일 설명변수(X)가 포함되지 않은 SARIMA 모델이다보니 더 정확도가 떨어진 것 같다.
R2-score가 계속 마이너스가 나오는데 왜 그러는지 모르겠다.

Try
다음에는 2년 이상의 데이터를 이용하고, 설명변수를 추가해 더 정확도를 높여보아야겠다. 또한, LSTM도 사용해 볼 것이다.

Keep
단기 예측(1달)의 정확도가 생각보다 높았다.
MAPE가 생각보다 낮았다.