📌 다익스트라 - Dijkstra

다익스트라는 음의 가중치가 없는 그래프의 한 정점에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘입니다.

최소 스패닝 트리에 사용되는 프림알고리즘과 매우 유사하기 때문에 프림알고리즘을 알고 있다면 이해가 쉬울껍니다.

물론 처음 다익스트라를 이해하는데 코드 하나하나를 순차적으로 보는것도 좋은 방법이지만
직관적으로 이해하기 위해서 최단경로 - 1753번 의 코드를 바로 살펴보겠습니다.

📌 코드

import sys,heapq
input=sys.stdin.readline

def Dijkstra(Node):

    dp[Node]=0

    heapq.heappush(heap,(0,Node))

    while heap:

        value,node=heapq.heappop(heap)

        if dp[node]<value:
            continue

        for next_value,next_node in graph[node]:

            next_value+=value

            if next_value<dp[next_node]:

                dp[next_node]=next_value
                heapq.heappush(heap,(next_value,next_node))


INF=int(1e9)

V,E=map(int,input().split())
K=int(input())
dp=[INF]*(V+1) ; heap=[] ; graph=[ [] for _ in range(V+1) ]

for _ in range(E):
    u,v,w=map(int,input().split())
    graph[u].append((w,v)) # 가중치 먼저

Dijkstra(K)

for i in range(1,V+1):

    if dp[i]==int(1e9):
        print("INF")
    else:
        print(dp[i])

전체 코드입니다. 중요한 부분만 하나씩 살펴봅시다.

INF=int(1e9)
dp=[INF]*(V+1) 

여기서 dp 는 노드들의 번호가 인덱스 값이고 배열의 값에 최단 경로를 저장합니다.

일단 배열의 초기값을 아주 큰 수로 잡았습니다.
왜냐하면 다익스트라는 이동가능한 새로운 정점을 찾을때
지금까지 연결한 가중치의 합이 새로운 정점보다 큰지 작은지 비교하기 위해서 입니다.

for _ in range(E):
    u,v,w=map(int,input().split())
    graph[u].append((w,v)) # 가중치 먼저

문제에서 주어지는 대로 u 와 v 의 단방향 노드가 연결되어있을때 가중치 w 가 있으면 이렇게 입력받습니다.

def Dijkstra(Node):
    dp[Node]=0
    heapq.heappush(heap,(0,Node))

다익스트라 함수를 실행하기 앞서 미리 해둬야 하는 부분입니다.
시작하는 부분을 가중치를 0 으로 잡습니다. 그리고 힙 자료구조를 사용하기 위해 시작점의 가중치 0 과 그떄의 노드번호를 넣어줍니다.

 while heap:
        value,node=heapq.heappop(heap)

        if dp[node]<value:
            continue

heap 배열이 없어질때까지 , 즉 더이상 이동할 경로가 없을때까지 반복해줍니다.
먼저 heappop 을 통해 가중치가 가장 적은 지점을 우선적으로 탐색해줍니다.
그리고 그때의 노드 번호도 저장합니다.

이때 dp[node]<value , 즉 다음번에 이동할 가중치가 지금까지 이동하는데 가중치의 합보다 크다면 이동하지 않는다. 라는 의미입니다.

for next_value,next_node in graph[node]:

	next_value+=value

	if next_value<dp[next_node]:

		dp[next_node]=next_value
        heapq.heappush(heap,(next_value,next_node))

만약 지금까지 이동한 거리의 합보다 다른 노드로 가는 간선이 더 짧다면 그 길로 이동해야겠죠?
그때 이동가능한 경로를 for next_value,next_node in grahp[node] 를 통해 이동가능한 경로를 가져옵니다.

그리고 next_value+=value 는 지금까지 이동한 경로의 합에 다음번에 이동할 가중치의 값을 더한다. 즉 다음번에 이동했을때 시작노드부터의 거리를 미리 저장한다는 의미입니다.

이후 next_value<dp[next_node] 즉 ,다음번에 이동했을때 시작노드부터의 거리가 이전에 이동했을때 필요했던 가중치보다 작다면 더 작은 값으로 갱신해주고 heappush 를 통해 다시 그 노드부터 경로를 탐색해줍니다.

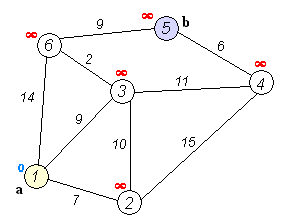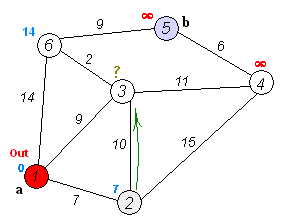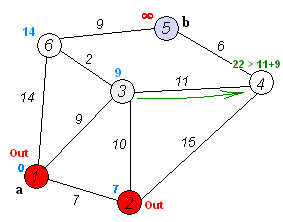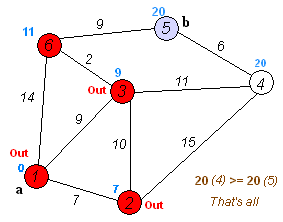
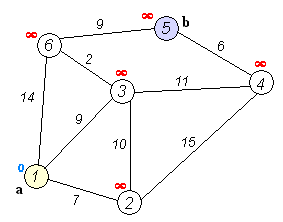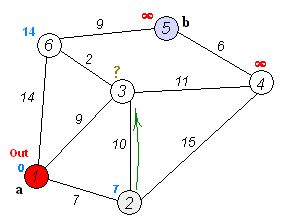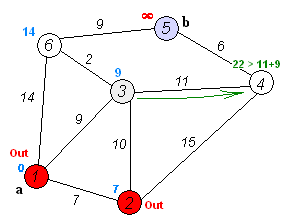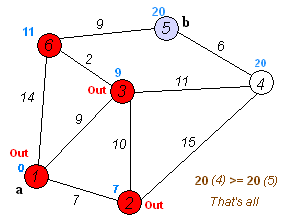
이 움짤을 보시면 더 이해하기 쉬울겁니다. 저는 이전에 크루스칼알고리즘과 프림알고리즘같은 최단경로알고리즘을 접한적이 있어 이해가 쉬웠는데 코드를 봐도 이해가 되지않는다면

바킹독 - 다익스트라 또는 나동빈 - 다익스트라 와 같은 영상을 보시는것을 추천합니다.

📌 시간복잡도

원래는 노드의 개수가 $V$ 개있고 간선의 개수가 $E$ 개 있으면 $O(V^2)$ 이 시간복잡도가 필요하지만 매번 최소값을 바로 구할수 있는 힙 자료구조를 사용하여 $O(E log V)$ 라는 시간복잡도로 다익스트라를 구현할 수 있습니다.

또한 만약 1부터 $N$ 까지의 최단경로를 구하기 위해서는 다익스트라를 한번만 구현해도 좋지만
그중에 3번 노드를 꼭 지나야 한다면 1부터 3까지의 최단경로 , 3부터 $N$ 까지의 최단경로를 두개다 구해서 더해주는 방법도 가능합니다.

이상으로 다익스트라 알고리즘에 대해 알아보았습니다.