최소 스패닝 트리 - Minimum Spanning Tree

📌 최소 스패닝 트리 , 최소 신장 트리 - $MST$ ( $Minimum$ $Spanning$ $Tree$ )

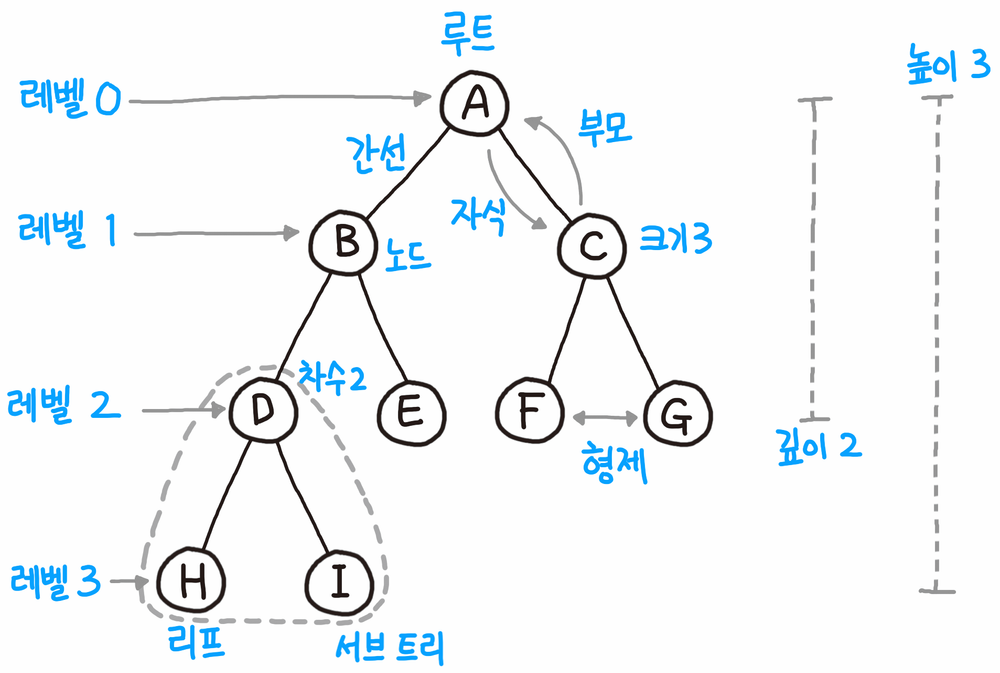
시작하기에 앞서 먼저 트리의 개념을 다시 살펴봅시다.

트리란 사이클이 없는 양방향 그래프 입니다. 그렇다면 최소 스패닝 트리란 무엇일까요?

최소 스패닝 트리란 트리를 구성하면서 모든 정점을 연결하되 , 가중치의 합이 최소가 되는 트리를 의미합니다.

위 사진에서 첫번째 그림의 트리가 있다고 가정해보겠습니다.

2 번째 그림은 스패닝 트리입니다. 즉 모든 정점을 연결하면서 사이클이 없기 때문이죠.

3 번째 그림은 스패닝 트리가 아닙니다. 모든 정점을 연결하지 못하기 때문이죠.

마지막 그림 또한 모든 정점을 연결할지라도 사이클이 존재하기 때문에 스패닝 트리가 아닙니다.

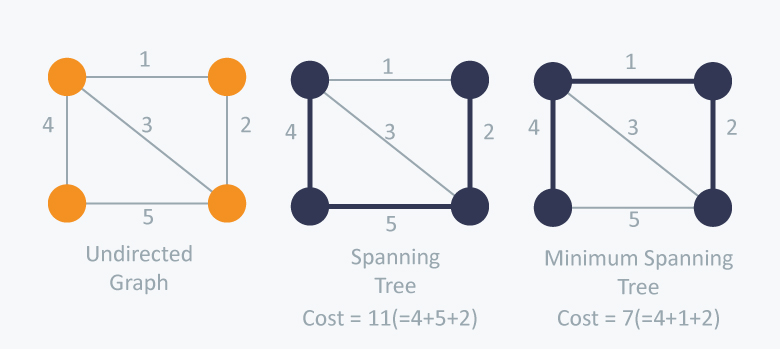
그래프에 가중치가 있다고 해봅시다. 이때 2번째 그림은 모든 정점을 연결하고 사이클이 없기 때문에 스패닝 트리가 맞습니다.

하지만 3 번째 그림처럼 연결하면 모든 정점을 연결하고 , 사이클이 없고 , 가중치의 합이 최소가 되기 때문에 최소 스패닝 트리 입니다.

📌 Kruskal Algorithm

그리디 알고리즘으로 분류되는 크루스칼 알고리즘에 대해 알아보겠습니다.

이는 최소스패닝 트리를 만드는 방법중 하나입니다.

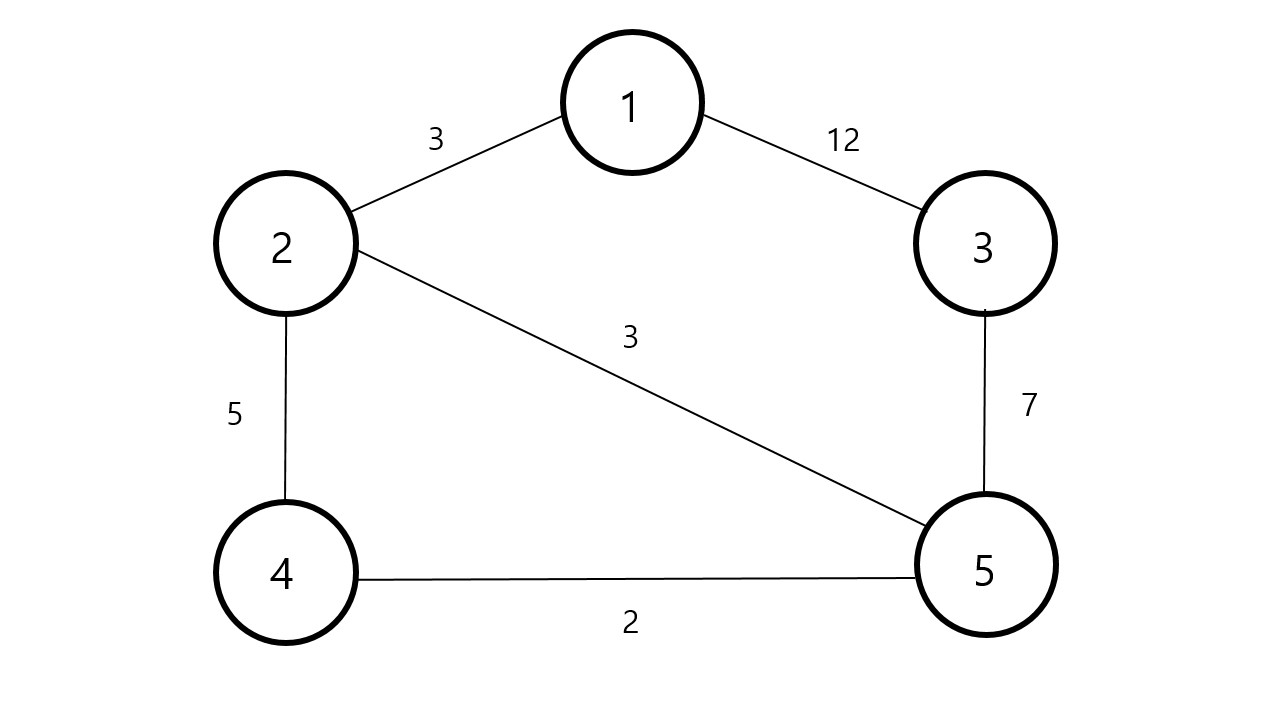
이런 그래프가 있다고 가정해봅시다. 우리가 만들것은 최소 스패닝 트리입니다. 즉 모든 정점을 연결하고 사이클이 없으며 가중치의 합이 최소인 트리를 만드는 것이 목표입니다.

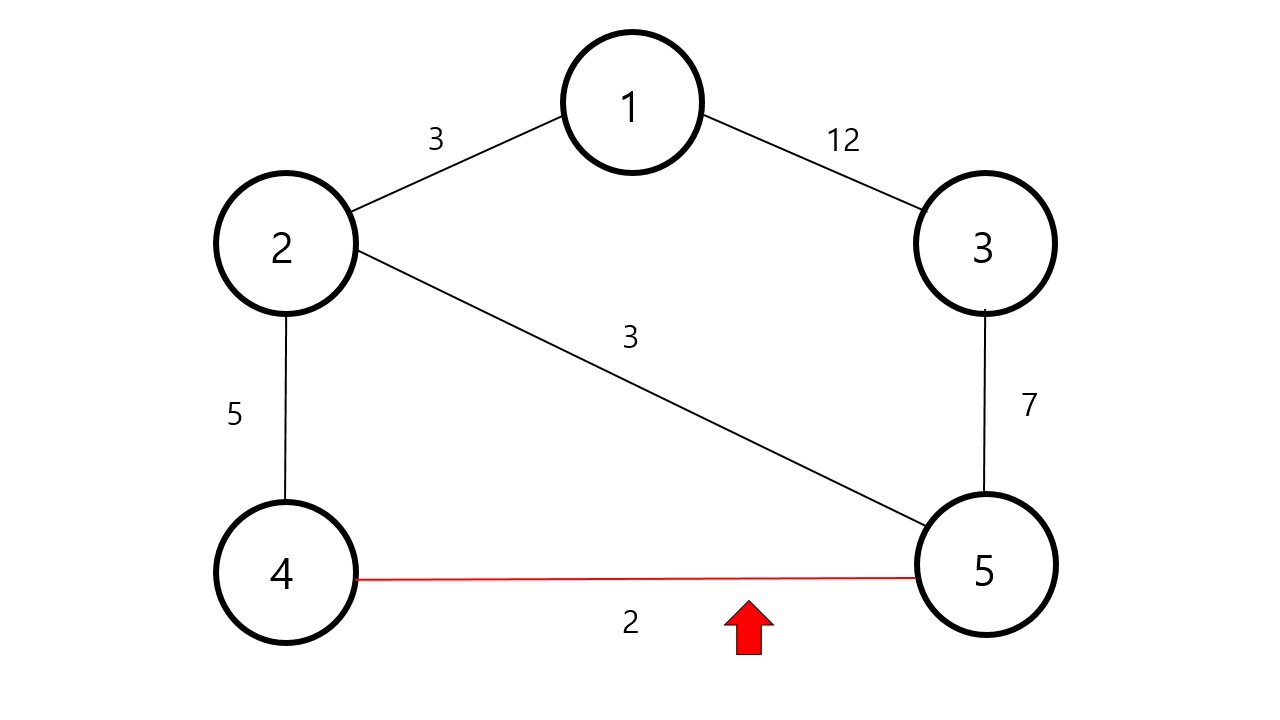
크루스칼 알고리즘은 모든 가중치 중에서 가장 작은 가중치를 먼저 탐색합니다.

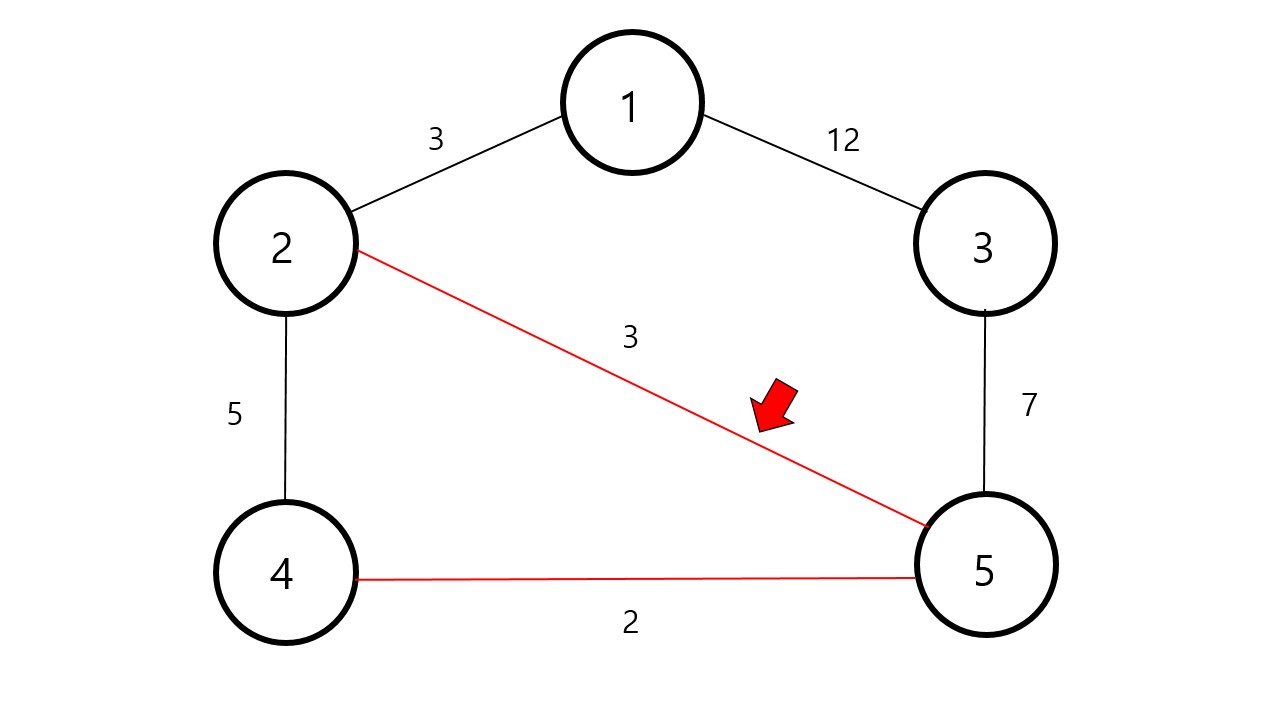
그다음으로 작은 가중치인 $3$ 을 연결해줍니다.

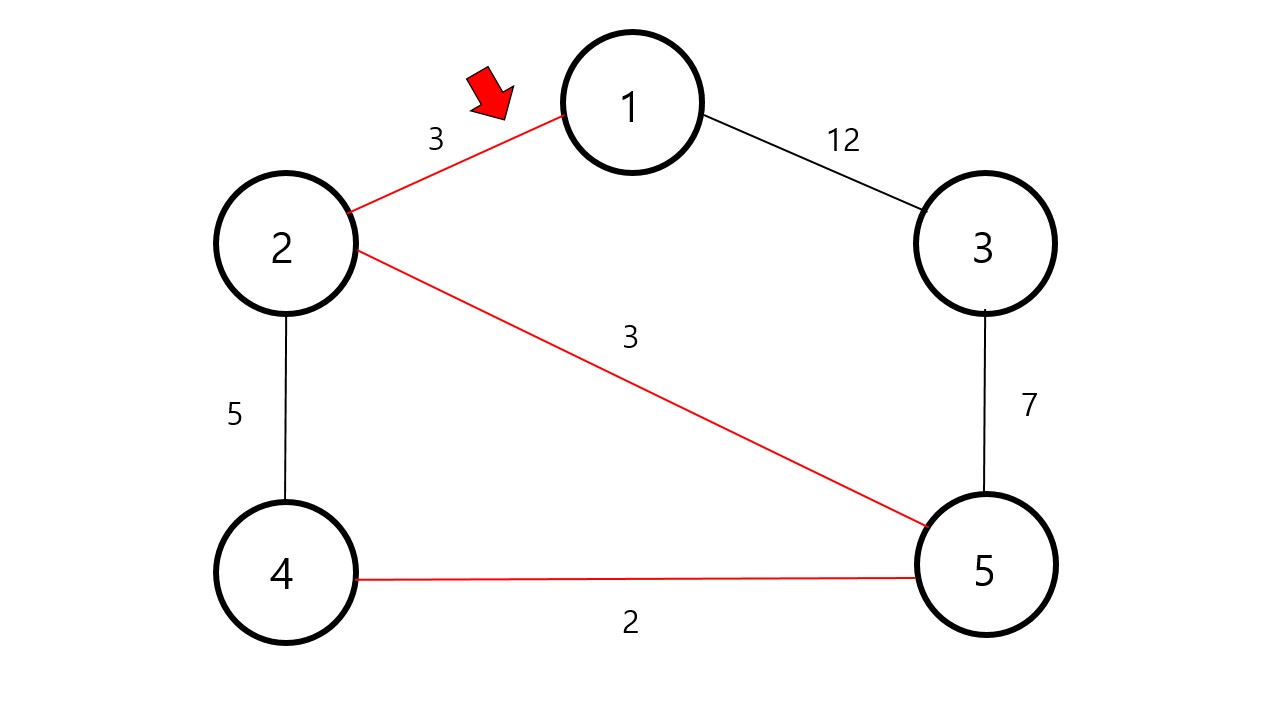
계속 연결해줍시다.

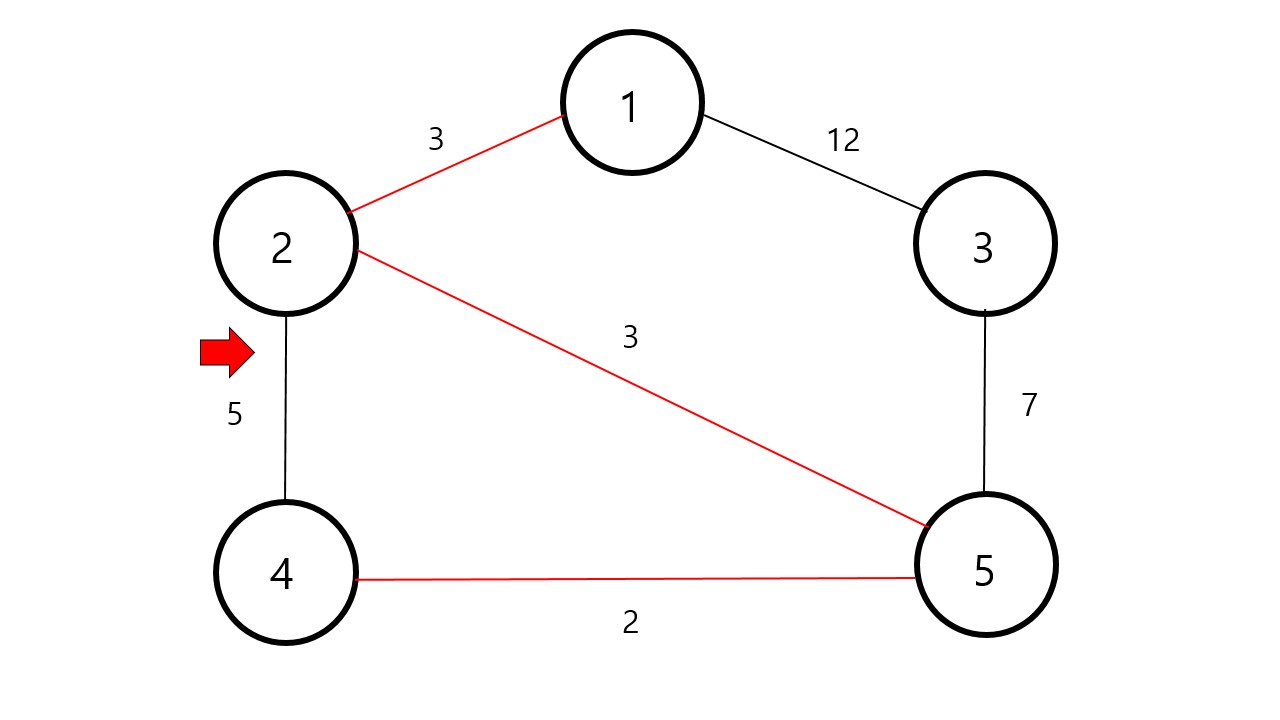
하지만 $5$ 는 연결할 수 없습니다. 왜냐하면 2-4-5 라는 사이클이 생기기 때문입니다. 이때는 연결하지않고 다음 가중치를 찾아줍니다.

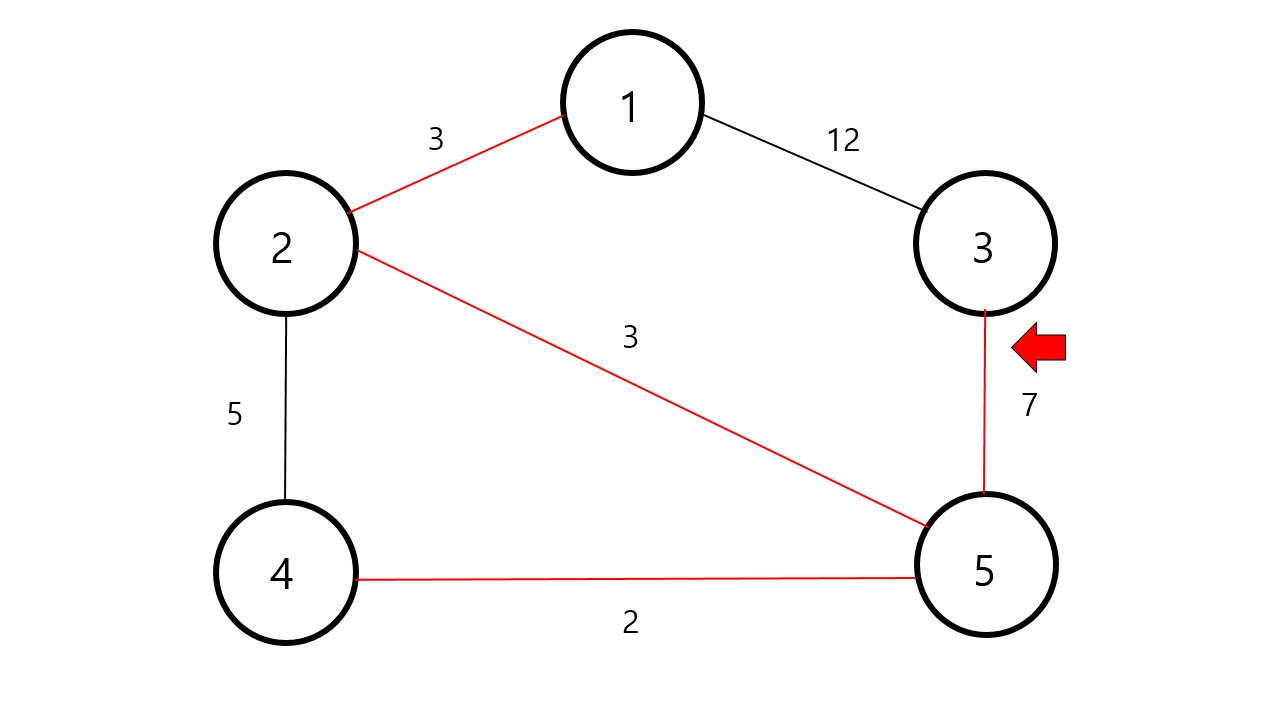
$7$ 은 연결해도 사이클이 생기지 않으므로 연결해 줍니다.

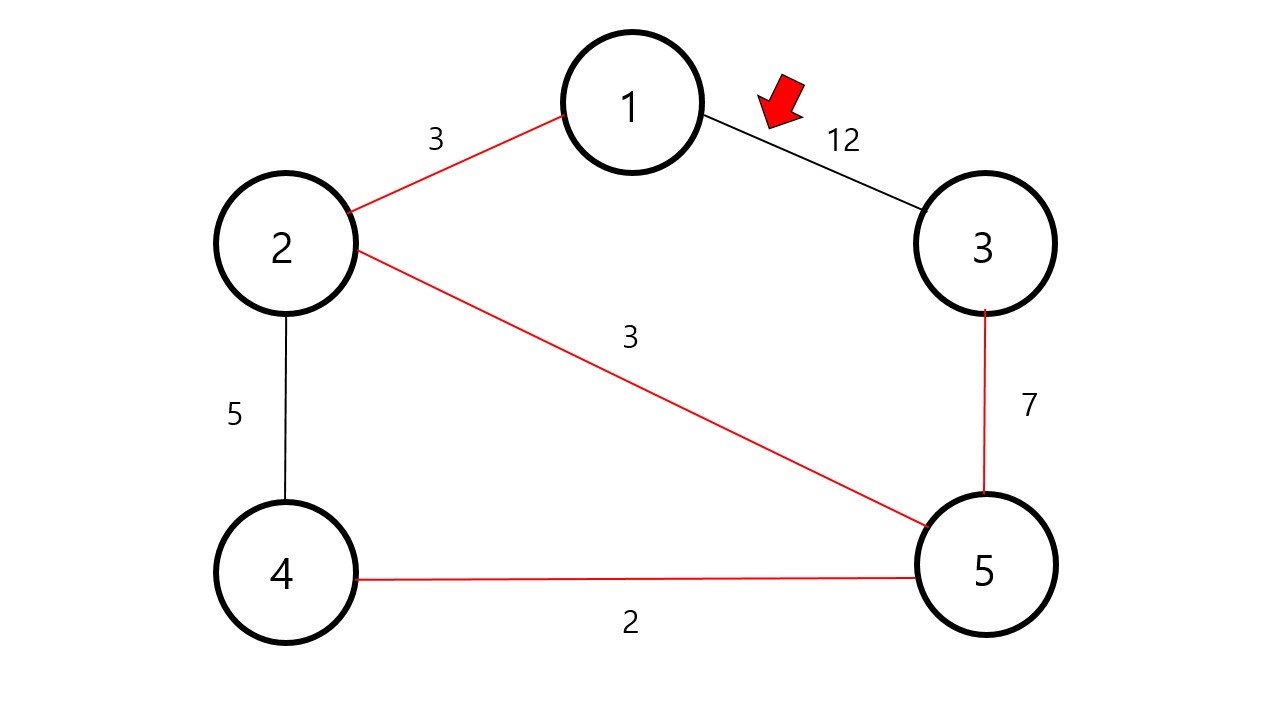
$12$ 는 연결하면 사이클이 생기므로 연결하지 않습니다.

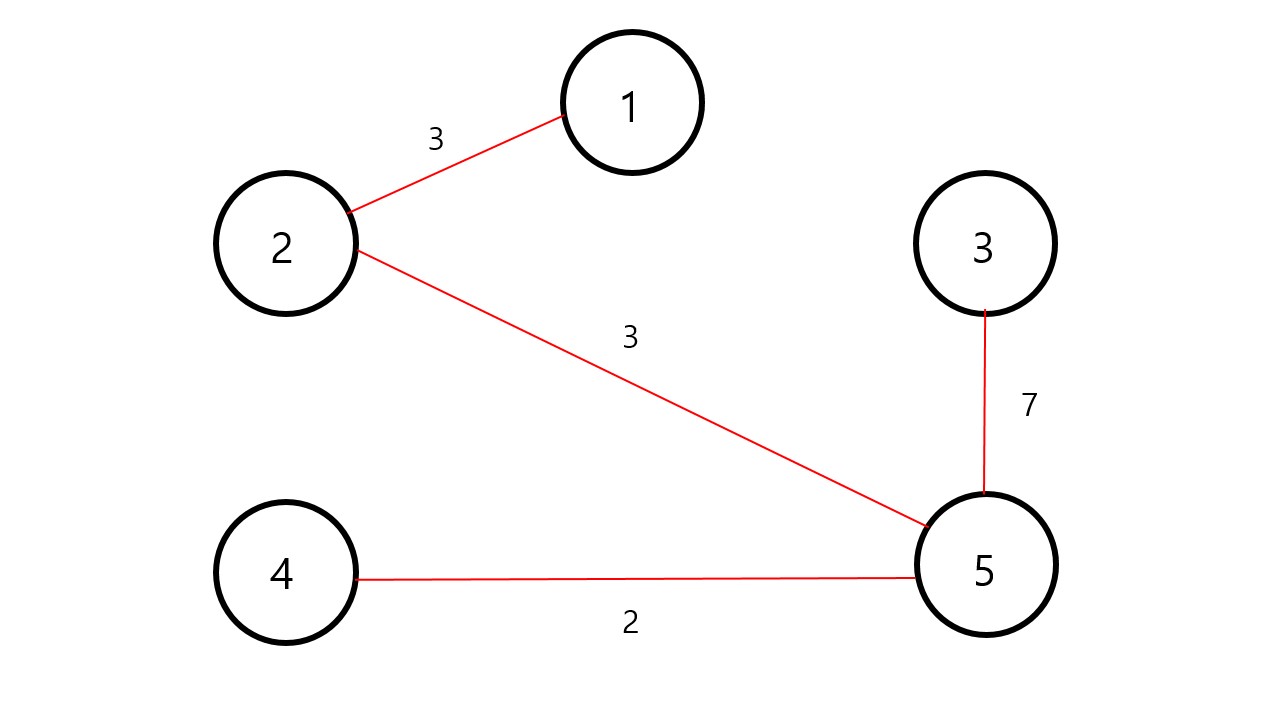
따라서 결론적으로 위 그림과 같은 최소 스패닝 트리를 구할 수 있습니다.

📌 Kruskal Algorithm - Code

문제 링크

import sys
input=sys.stdin.readline

def Find(x): #같은 집합에 속하는지 유니온 파인드로 확인한다.

    if x!=disjoint[x]:
        disjoint[x]=Find(disjoint[x])
    return disjoint[x]


V,E=map(int,input().split()) 

disjoint=[ i for i in range(V+1) ] # 유니온 파인드 리스트

MST=[] # 입력받을 리스트

for i in range(E):
    MST.append(list(map(int,input().split())))

MST.sort(key=lambda x:x[2]) #가중치에 대해서 정렬 해준다.

value=0 #가중치의 합을 담을 변수

for U,V,K in MST:

    U=Find(U)
    V=Find(V)

    if U!=V: # 만약 두 정점이 같은 집합에 속하지 않다면 연결해준다.
        if U>V: # 노드 번호가 더 작은 것을 기준으로 연결해준다.
            disjoint[U]=V
        else:
            disjoint[V]=U
            
        value+=K # 가중치를 더해준다.

print(value) # 가중치의 최소값 출력

파이썬 코드입니다. 중요한 부분은 가중치에 대해서 그래프를 정렬 해준다는 점과 유니온 파인드를 사용해서 두 정점이 같은 집합에 있는지 확인해준다는 점입니다.

정점의 개수 $V$ 와 간선의 개수 $E$ 라고 하였을때 $Union$-$Find$ 알고리즘은 $O(1)$ 즉 상수 시간 복잡도를 가지기 때문에 크루스칼 알고리즘은 $O(E log E)$ 의 시간복잡도를 가집니다.

📌 Prim Algorithm

이번에는 최소 스패닝 트리를 구하기 위한 방법으로 프림 알고리즘에 대해 알아보겠습니다.

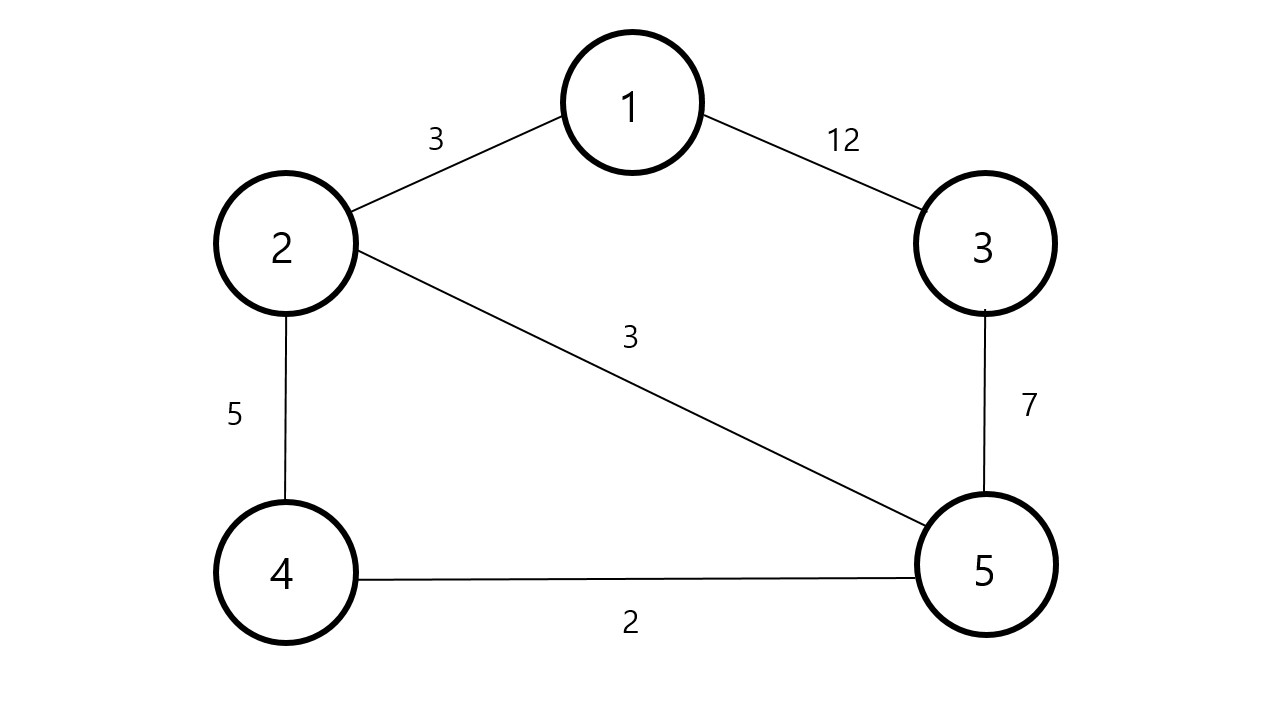
아까와 같은 그래프가 있다고 가정해봅시다. 이때 임의의 정점 하나를 택해줍니다.

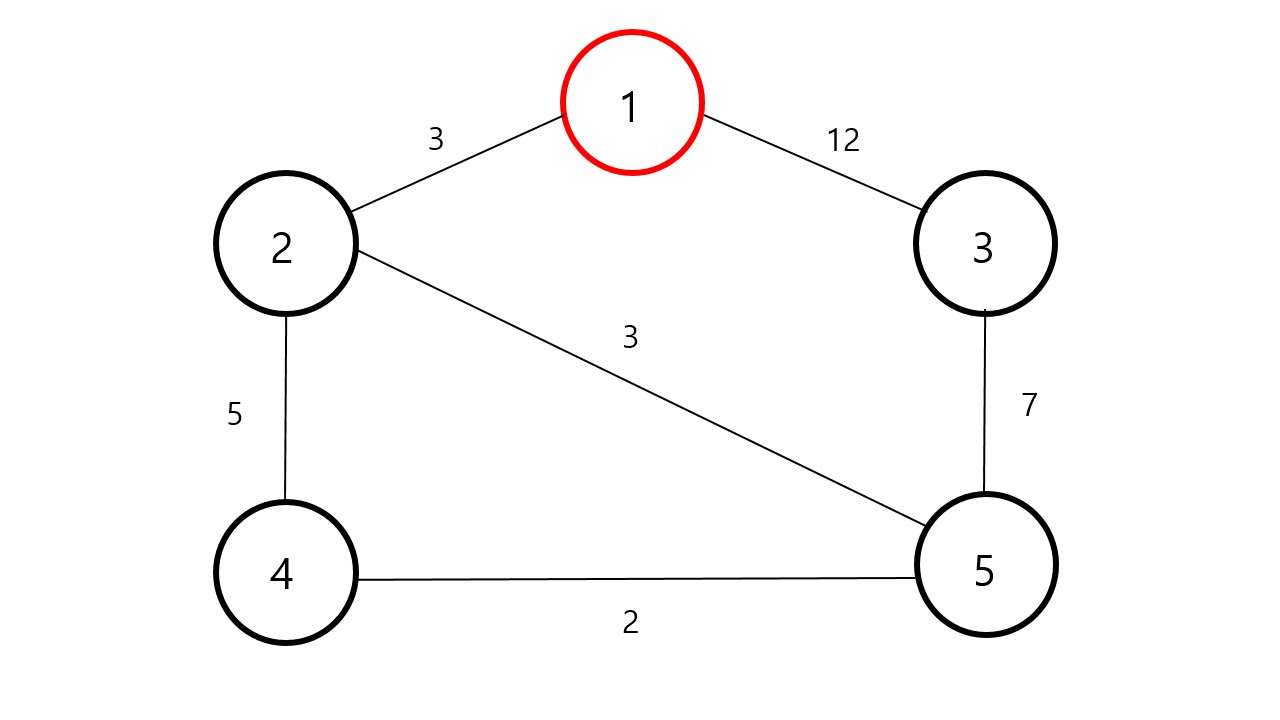
$1$ 을 선택했습니다. 그리고 갈 수 있는 정점들 중에서 가중치의 값이 가장 적은 노드부터 우선 탐색합니다. 지금 갈 수 있는 노드는 $2$ 번 노드와 $3$ 번 노드이기 때문에 가중치가 더 적은 $2$ 번 노드를 선택합니다.

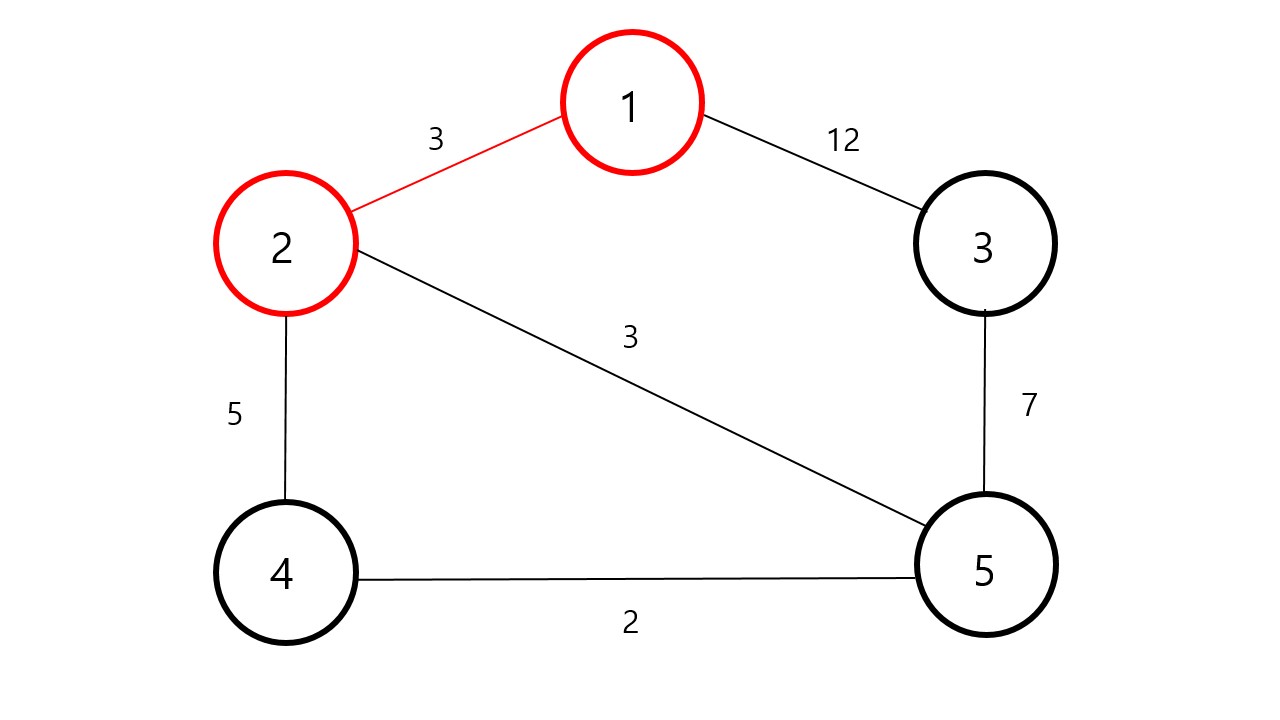
이제 $4$ 번 노드 , $3$ 번 노드 , $5$ 번 노드를 갈 수 있습니다. 가중치가 가장 적은 값이 $3$ 이므로 $5$ 번 노드를 먼저 탐색해줍니다.

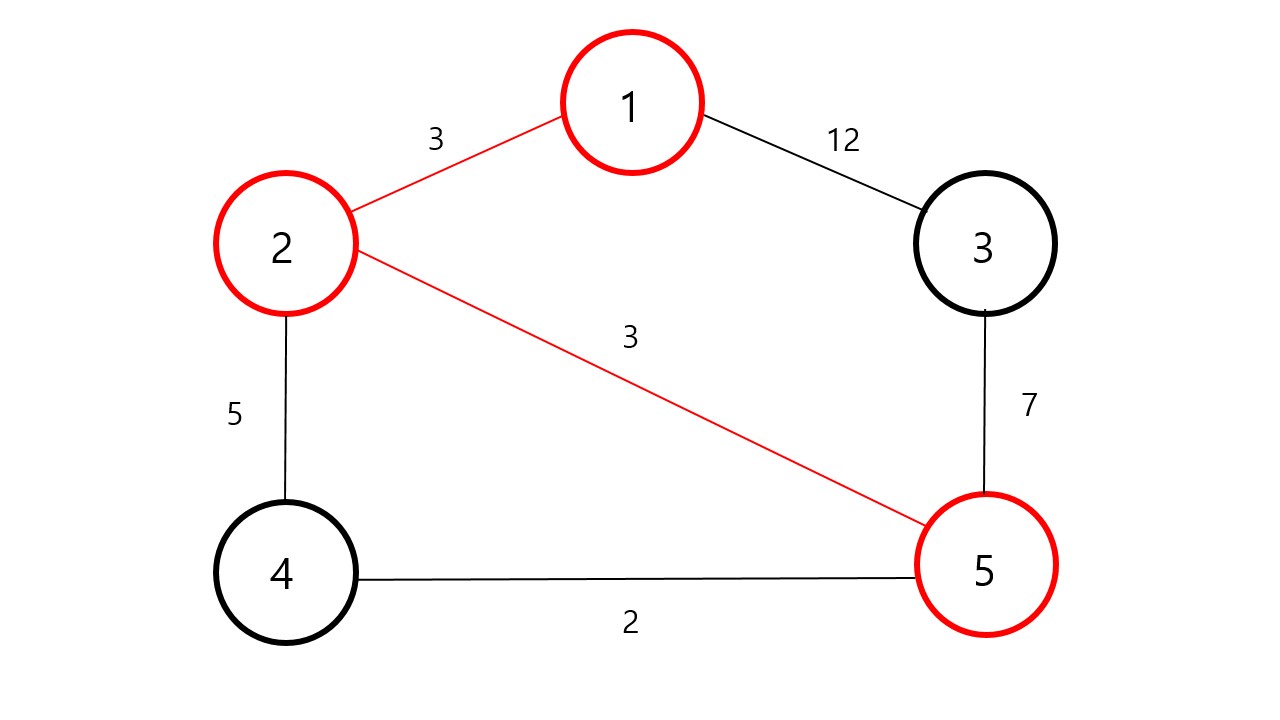
마지막으로 가중치의 값이 가장적은 $4$ 번 노드를 선택해줍니다.

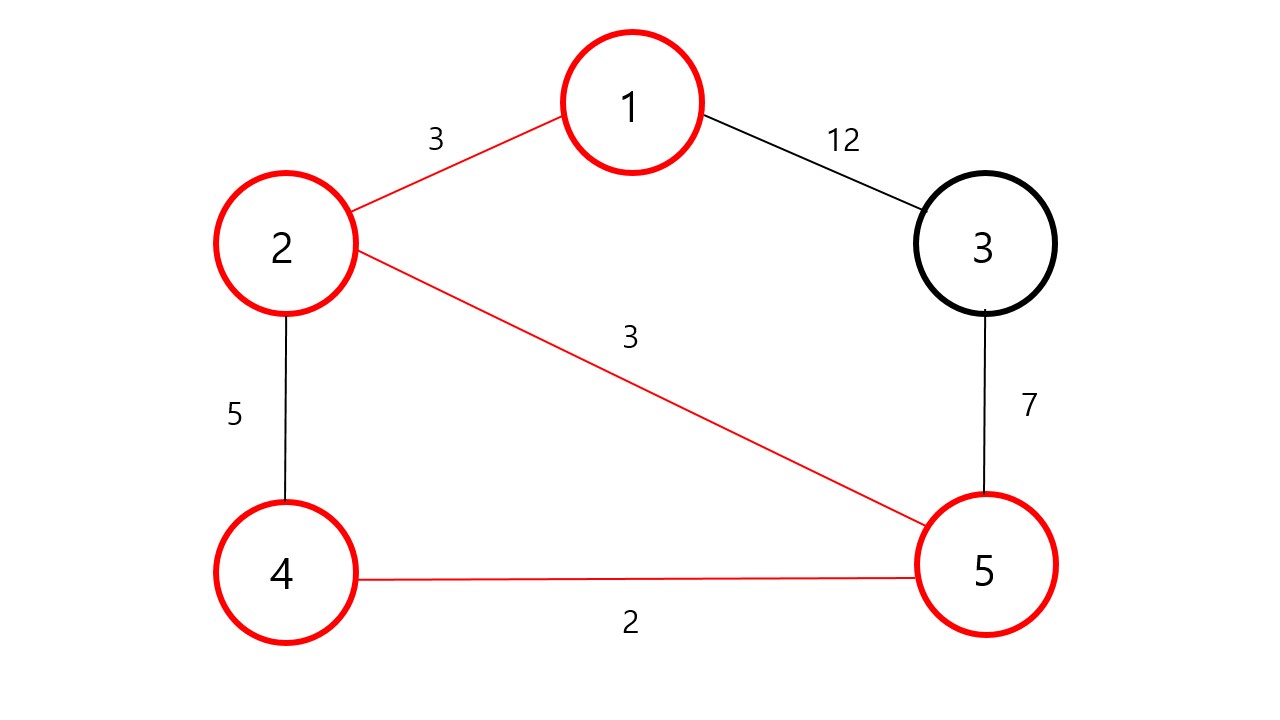
이제 다른 정점을 선택하면 사이클이 무조건 생깁니다. 따라서 여기까지 연결하고 끝냅니다.

따라서 결론적으로 위 그림과 같은 최소 스패닝 트리를 구할 수 있습니다.

📌 Prime Algorithm - Code

문제 링크

import sys,heapq #힙 사용
input=sys.stdin.readline

V,E=map(int,input().split())

visit=[False]*(V+1) #방문 처리 배열

MST=[ [] for _ in range(V+1) ]
heap=[ [0,1] ] # 힙

for i in range(E):
    s,e,w=map(int,input().split())

    MST[s].append([w,e])
    MST[e].append([w,s])


value=0 #가중치를 담을 변수

while heap:

    w,s=heapq.heappop(heap) # 가중치가 가장 적은 값과 노드번호를 받는다.

    if not visit[s]: # 만약 방문하지 않은 지점이라면
        visit[s]=True #방문처리
        value+=w # 가중치 추가

        for i in MST[s]:
            heapq.heappush(heap,i) # 갈 수 있는 다른 노드들을 추가한다.

print(value)

프림 알고리즘을 사용할때는 최소값이 매번 필요하기 때문에 heap 자료구조를 사용합니다. 또한 방문 처리를 하기 위해서 visit 배열을 통해 방문 처리를 해줍니다.

정점의 개수 $V$ 와 간선의 개수 $E$ 라고 하였을때 시간복잡도는 $O(E logV)$ 입니다.

✅ 어떤 알고리즘을 써야하는가?

프림의 시간 복잡도는 $O(ElogV)$ 이고 크루스칼의 시간 복잡도는 $O(ElogE)$ 이기 때문에

그래프 내의 간선이 많은 경우는 프림 알고리즘, 간선이 적은 경우는 크루스칼 알고리즘이 유리합니다.

지금까지 최소신장트리를 알아보았고 그것을 구현하기 위한 크루스칼 알고리즘 , 프림 알고리즘에 대해 알아봤습니다.