백준 13418 : 학교 탐방하기 (Python)

본문 링크

📌 크루스칼 알고리즘

"""
0-오르막길에 대해 정렬하고
1-내리막길에 대해 정렬해서
2번 MST 구성.
"""
import sys
input=sys.stdin.readline

def Find(x):

    if x!=disjoint[x]:
        disjoint[x]=Find(disjoint[x])
    return disjoint[x]

N,M=map(int,input().split())

edge=[]
for i in range(M+1): # 간선은 M+1 개 입력받는다.

    A,B,C=map(int,input().split())

    edge.append((C,B,A))

edge.sort(key=lambda x:x[0])
disjoint=[ _ for _ in range(N+1) ] ; Zero=0 ; One=0 ; check_Zero=0 ; check_One=0

for value,x,y in edge:

    x=Find(x)
    y=Find(y)

    if x!=y:
        if x>y:
            disjoint[x]=y
        else:
            disjoint[y]=x
        if value==0:
            check_Zero+=1


edge.sort(key=lambda x:-x[0])
disjoint=[ _ for _ in range(N+1) ]

for value,x,y in edge:

    x=Find(x)
    y=Find(y)

    if x!=y:
        if x>y:
            disjoint[x]=y
        else:
            disjoint[y]=x
        if value==0:
            check_One+=1

print(check_Zero**2- check_One**2)

📌 프림 알고리즘

import sys,heapq
input=sys.stdin.readline

N,M=map(int,input().split())

Tree_Zero=[ [] for _ in range(N+1) ]
Tree_One=[ [] for _ in range(N+1) ]

for i in range(M+1):

    A,B,C=map(int,input().split())

    Tree_Zero[A].append((C,B))#가중치 먼저
    Tree_Zero[B].append((C,A))

    Tree_One[A].append((-C,B)) #최대힙
    Tree_One[B].append((-C,A))

visit=[False]*(N+1) ; heap=[(0,0)]
check_Zero=0 ; check_One=0

while heap:

    value,node=heapq.heappop(heap)

    if not visit[node]:

        if value==0:
            check_Zero+=1
        visit[node]=True

        for i,j in Tree_Zero[node]:
            heapq.heappush(heap,(i,j))

visit=[False]*(N+1) ; heap=[(0,0)]

while heap:

    value, node = heapq.heappop(heap)

    if not visit[node]:

        if value==0:
            check_One+=1
        visit[node] = True

        for i, j in Tree_One[node]:
            heapq.heappush(heap, (i, j))


print( (check_Zero-1)**2-(check_One-1)**2)

📌 어떻게 접근할 것인가?

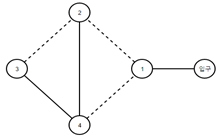
최소 스패닝 트리 문제입니다. 간단하게 정렬을 통해서 내리막길을 먼저 연결해주는 방법과 오르막길을 먼저 연결해주는 스패닝 트리를 만들어 주었습니다.

이때 피로도 계산은 오르막길일때만 생각해주면 되고 입력을 받을때 $M$ 번이 아니라 총 $M+1$ 번을 받아야합니다.

또한 최대 피로도의 제곱에 최소피로도의 제곱을 빼야지 답이 나옵니다.

프림 알고리즘에서 최대힙과 최소힙을 사용하였고 , -1$ 을 한 이유는 힙에서 시작을 $0$ , 즉 오르막길을 시작으로 해서 마지막에 $-1$ 를 해주었습니다.