백준 16202 : MST 게임 (Python)

본문 링크

📌 크루스칼 알고리즘

"""
2<=N<=1000 이기 때문에 완탐가능.
입력하는 간선의 순서대로 가중치가 1씩증가하기 때문에
간선을 저장해두었다가 popleft 로 하나씩 가장 작은 간선을 제거해서
다시 트리를 만들어 보고 최소 스패닝 트리가 되는지 확인한다.
"""
import sys
input=sys.stdin.readline
from collections import deque

def Find(x):

    if x!=disjoint[x]:
        disjoint[x]=Find(disjoint[x])
    return disjoint[x]

N,M,K=map(int,input().split())

edge=deque()

for i in range(M):

    u,v=map(int,input().split())

    edge.append((i+1,u,v))

for i in range(K):

    disjoint = [_ for _ in range(N + 1)] ; total=0

    for j in range(len(edge)):

        x=Find(edge[j][1])
        y=Find(edge[j][2])

        if x!=y:
            if x>y:
                disjoint[x]=y
            else:
                disjoint[y]=x
            total+=edge[j][0]

    check=set()

    for j in range(1,N+1):

        if Find(j) not in check:
            check.add(Find(j))

    if len(check)>1:
        print(0 , end=" ")
    else:
        print(total, end=" ")
    edge.popleft()

📌 프림 알고리즘

import sys,heapq
input=sys.stdin.readline
from collections import deque

N,M,K=map(int,input().split())

edge=deque()

for i in range(M):

    u,v=map(int,input().split())
    edge.append((i+1,u,v))

for i in range(K):

    visit=[False]*(N+1) ; heap=[(0,1)] ; Tree=[ [] for _ in range(N+1)] ; total=0
    for j in range(len(edge)):

        value,u,v=edge[j][0],edge[j][1],edge[j][2]

        Tree[u].append((value,v))
        Tree[v].append((value,u))

    while heap:

        value,node=heapq.heappop(heap)

        if not visit[node]:

            visit[node]=True
            total+=value

            for Tree_value,Tree_node in Tree[node]:
                heapq.heappush(heap,(Tree_value,Tree_node))

    if visit[1:].count(False)>0:
        print(0 , end=" ")
    else:
        print(total , end=" ")

    edge.popleft()

📌 어떻게 접근할 것인가?

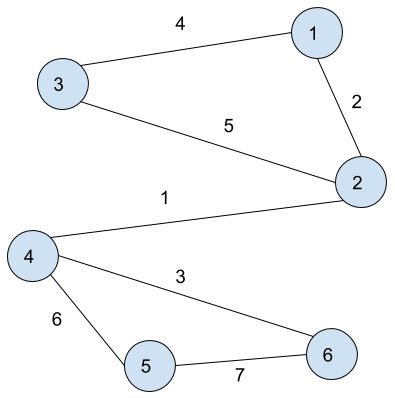
문제는 간단합니다. 입력으로 서로 연결되어있는 정점이 주어집니다. 이때 입력으로 주어지는 순서에 따라 가중치가 1씩 증가합니다.

그리고 가장 가중치가 낮은 , 즉 가장 먼저 받은 간선들을 잘라서 $MST$ 가 완성되는지 확인하고 , 가능하다면 가중치의 합의 최소값을 구하면됩니다.

이때 $N$ 의 범위가 $2 ≤ N ≤ 1,000$ 이기 때문에 완전탐색이 가능합니다.

따라서 매번 크루스칼 , 프림알고리즘을 돌려주고 덱을 이용하여서 popleft 로 가장 최근에 입력받은 원소를 하나씩 $K$ 번 제거 해줍니다.

그리고 가중치의 합의 최소값을 출력해줍니다.