
import sys
input=sys.stdin.readline
from itertools import combinations
LMI=lambda:list(map(int,input().split()))
MI=lambda:map(int,input().split())
G=lambda x:[ LMI() for _ in range(x) ]
V=lambda x,y:[ [False]*y for _ in range(x) ]
def Ladder(P):
Ladder_graph=[ i[:] for i in graph]
for x,y in P:
Ladder_graph[x][y]=y+2
Ladder_graph[x][y+1]=y+1
total = 0
for i in range(N):
x,y=[0,i]
while True:
if x==H:
if y==i:
total+=1
break
else:
return False
if Ladder_graph[x][y]:
y=Ladder_graph[x][y]-1
x+=1
else:
x+=1
if total==N:
return True
return False
N,M,H=MI()
graph=[ [0]*N for _ in range(H+1) ]
L=[] ; P=[]
for i in range(M):
a,b=MI()
graph[a-1][b]=b
graph[a-1][b-1]=b+1
for i in range(H+1):
for j in range(1,N):
if [graph[i][j-1],graph[i][j]]==[0,0]:
L.append((i,j-1))
if Ladder([]):
print(0)
exit(0)
for i in range(len(L)):
if Ladder([L[i]]):
print(1)
exit(0)
for i in combinations(L, 2):
if Ladder(i):
print(2)
exit(0)
for i in combinations(L,3):
if Ladder(i):
print(3)
exit(0)
print(-1)📌 어떻게 접근할 것인가?
오랜만에 푸는데 엄청 오래걸린 문제였습니다. 6시간정도 푼것같습니다.
이 문제를 풀면서 새로얻은 지식도 많은것같네요. 좋은문제인것같습니다.
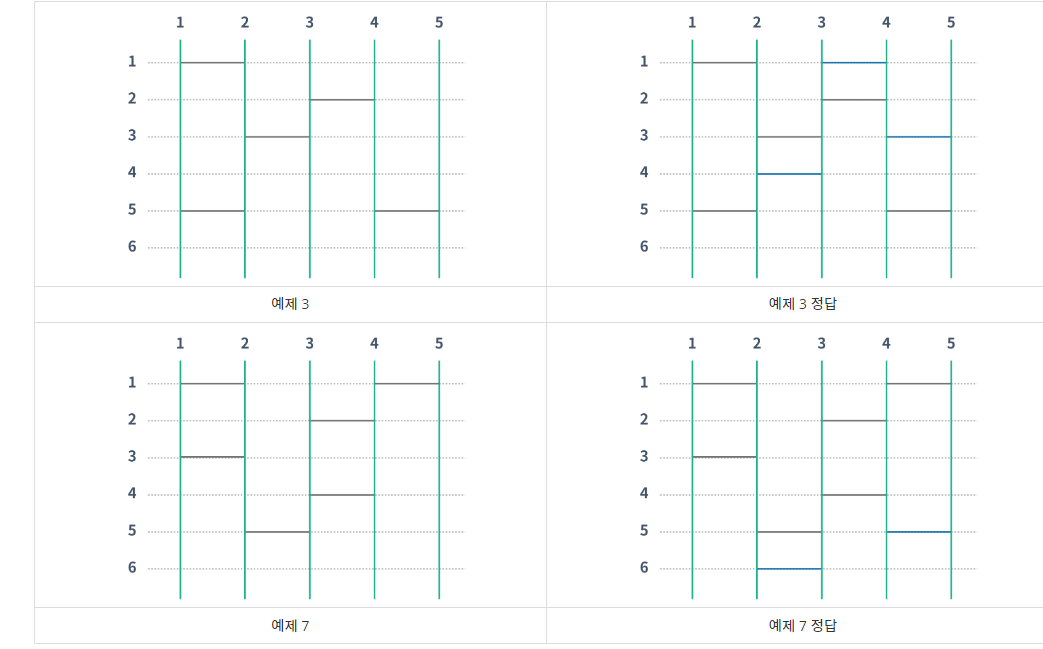
문제는 간단합니다.
사다리에 다리를 3개까지 놓아서 번째 사다리에서 출발해서 번지점에 도착하도록 만드는 것입니다.
일단 , , 라는 변수가 주어졌는데 처음에 입력이 이해가안됬습니다.
은 가로길이 , 는 세로길이 , 은 초기에 놓아지는 사다리의 개수입니다.
graph=[ [0]*N for _ in range(H+1) ]따라서 배열의 길이는 이렇게 설정해주고
MI=lambda:map(int,input().split())
for i in range(M):
a,b=MI()
graph[a-1][b]=b
graph[a-1][b-1]=b+1총 번 동안 사다리를 미리 놓아주었습니다.
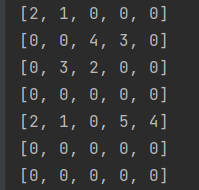
따라서 예제 3번을 입력했을때 그래프의 상태는 위와같습니다.
높이는 인덱스 관리가 편하게 하나 더 크게 잡아줬습니다.
그래프를 어떻게 구현할지에 대해 가장많은 시간을 썼던것같았습니다.
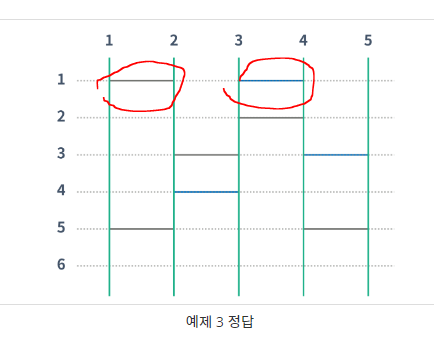
만약 가로의 길이를 으로 잡았을때 , 같은 줄에 1과2 , 3,4의 사다리가있을때
사다리를 전부 1 로 설정해버리면 [1,1,1,1,0] 과 같이 됩니다. 따라서 2번줄에서 시작을 하면 왼쪽으로 가야할지 오른쪽으로 가야할지 구분이 안됩니다.
그렇다고 [1,1,0,0,1,1,0,0] 이렇게 배열의 길이를 2배로 늘려버리면 하나의 점에서 탐색하기 때문에 인덱스 2 인부분에서 왼쪽사다리를 탈지 오른쪽 사다리를탈지 명확하지 않습니다.
따라서 그래프 자체에 가로인덱스 값을 넣어서 위치를 잡아주었습니다.

다시 그림을 보면 첫번째 줄애 [2,1,0,0,0] 은 0번째인덱스는 2-1 번째 인덱스로 가야한다는 뜻이고 1번째인덱스는 1-1 번째인덱스로 가는걸로 설정해서
[2,1,4,3,0] - 이처럼 한줄에 사다리가 2개가 있을경우도 제대로 탐색가능하게됩니다.
for i in range(H+1):
for j in range(1,N):
if [graph[i][j-1],graph[i][j]]==[0,0]:
L.append((i,j-1))초기 번의 입력을 받고 사다리를 설정한 다음에 사다리를 놓을 수 있는 지점의 인덱스를 모두 리스트에 담았습니다.
for i in combinations(L, 2):
if Ladder(i):
print(2)
exit(0)이후 콤비네이션을 통해서 사다리를 놓을 수 있는 모든지점중 2개를 선택하는 경우를 구했습니다.
def Ladder(P):
Ladder_graph=[ i[:] for i in graph]
for x,y in P:
Ladder_graph[x][y]=y+2
Ladder_graph[x][y+1]=y+1
total = 0
for i in range(N):
x,y=[0,i]
while True:
if x==H:
if y==i:
total+=1
break
else:
return False
if Ladder_graph[x][y]:
y=Ladder_graph[x][y]-1
x+=1
else:
x+=1
if total==N:
return True
return False사다리 탐색 부분입니다.
Ladder_graph=[ i[:] for i in graph]원래는 2차원 배열을 복사할때 deepcopy 를 사용했는데 , 슬라이싱과 컴프리헨션을 사용하는게 매우 빠릅니다. 이번에 처음알았는데 속도차이가 꽤 났습니다. 깊은복사를 사용하면 시간초과가 발생합니다.
for x, y in P:
Ladder_graph[x][y] = y + 2
Ladder_graph[x][y + 1] = y + 1모든 경우의 수에 대해서 0~3 개의 사다리를 놓아주었습니다.
total = 0
for i in range(N):
x,y=[0,i]
while True:
if x==H:
if y==i:
total+=1
break
else:
return False
if Ladder_graph[x][y]:
y=Ladder_graph[x][y]-1
x+=1
else:
x+=1
if total==N:
return True
return False시작은 제일 위에서 시작하고 사다리를 타고 가면서 만약 사다리 타기가 끝났을때 위치가 변동되었다면 바로 return False 를 해주었습니다. 만약 위치가 그대로였다면 total 변수에 1 을 추가하고 다음 위치에서 다시 사다리를 타고갑니다.
이후 total 변수가 과 값이 같다면 i 번째 사다리에서 시작해서 모두 i 번째 도착점으로 도달한다는 뜻이므로 True 를 반환합니다.
if Ladder([]):
print(0)
exit(0)
for i in range(len(L)):
if Ladder([L[i]]):
print(1)
exit(0)
for i in combinations(L, 2):
if Ladder(i):
print(2)
exit(0)
for i in combinations(L,3):
if Ladder(i):
print(3)
exit(0)
print(-1)사다리는 최대 3개 까지 놓을 수 있기 때문에 1개놓았을때 , 2개놓았을때 , 3개놓았을때 모두 구했습니다.
처음에 그래프만 잘 잡아줬다면 금방풀었을텐데 그래프를 어떻게 구성할지에 시간을 많이 썼습니다.
또 모든 경우의 수도 처음엔 백트래킹을 사용했는데 파이썬은 재귀가 너무 느리니깐 가능하면 itertools 를 쓰는게 좋을거같네요.