백준 15685 : 드래곤 커브 (Python)

본문 링크

import sys
input=sys.stdin.readline

LMI=lambda:list(map(int,input().split()))
MI=lambda:map(int,input().split())
G=lambda x:[ LMI() for _ in range(x) ]
V=lambda x,y:[ [False]*y for _ in range(x) ]

graph=[ [0]*101 for _ in range(101) ]

dx=[0,-1,0,1]
dy=[1,0,-1,0]
direction=[ [(0,1) , (-1,0)] , [(-1,0) , (0,-1)] , [(0,-1) , (1,0)] , [(1,0) , (0,1)] ]
N=int(input())
L=[]
for i in range(N):
    y,x,d,g=MI() #입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다.
    if g==0:
        graph[x][y]=graph[x+dx[d]][y+dy[d]]=1
    else:
        Q=[]
        while g:
            if not Q:
                graph[x][y]=1
                for j in range(2):
                    x+=direction[d][j][0] ; y+=direction[d][j][1]
                    graph[x][y]=1

                if d==0:
                    Q.append([3,1]) # 두번재 값인 0 은 정방향 , 1은 역방향.
                else:
                    Q.append([d-1,1])
                g-=1
            else:
                P=[]

                for j in range(1,len(Q)+1):
                    d=Q[-j][0]
                    if Q[-j][1]==0: # 정방향이라면.
                        if d==0:
                            P.append([3,1])
                        else:
                            P.append([d-1,1])
                        for k in range(2):
                            x+=direction[d][k][0] ; y+=direction[d][k][1]
                            graph[x][y]=1
                    else: # 역방향이라면
                        if d == 0:
                            P.append([3, 0])
                        else:
                            P.append([d - 1, 0])
                        for k in range(-1,-3,-1):
                            x -= direction[d][k][0] ; y -= direction[d][k][1]
                            graph[x][y] = 1
                for a,b in P:
                    Q.append([a,b])
                g-=1


total = 0
for i in range(1,101):
    for j in range(1,101):
        if [graph[i-1][j-1],graph[i-1][j],graph[i][j-1],graph[i][j]]==[1,1,1,1]:
            total+=1
print(total)

📌 어떻게 접근할 것인가?

엄청 어려웠던 문제였습니다. 조금만 더 접근을 달리했으면 쉽게 풀었을텐데 아쉽네요.

크게 2가지 방법이 있습니다. 0 세대를 기준으로 탐색하는 방법 , 1세대를 기준으로 탐색하는 방법입니다.

일단 더 간단한 0 세대를 기준으로 탐색하는 방법에 대해 알아보겠습니다.
위 코드는 1세대를 기준으로 풀이한 코드입니다.

📌 0 세대

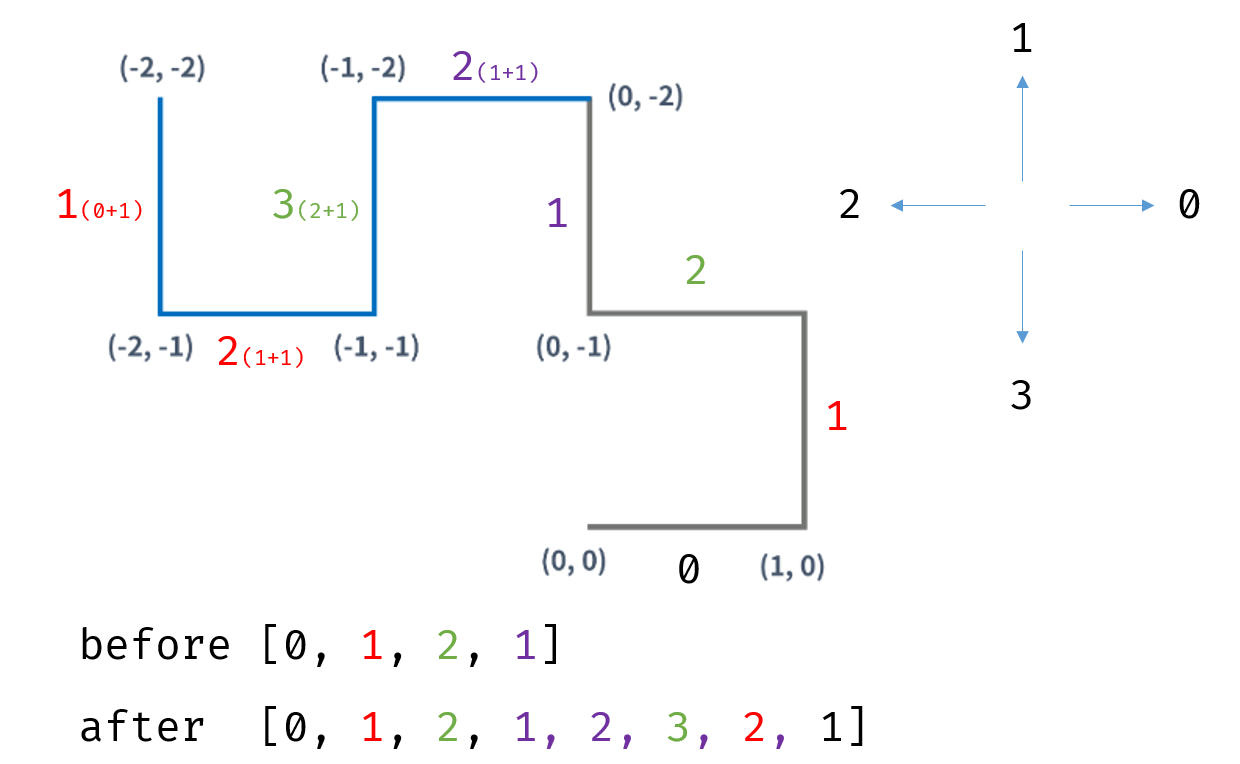
예제입력 1 의 그림입니다.

상하좌우를 [0,1,2,3] 으로 방향을 잡은 뒤 상하좌우에 따라서 이동을 합니다.

이 모양이 어떻게 만들어 졌는지 봅시다.

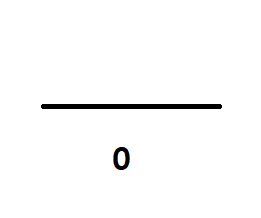
우측방향을 0 으로 잡고 0세대의 모양입니다.

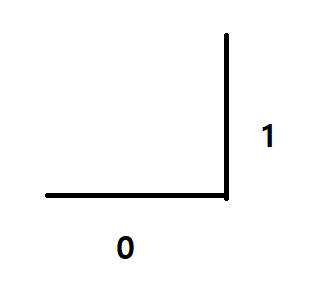
이후 이전의 방향에 +1 을 해서 위로 이동해줍니다.

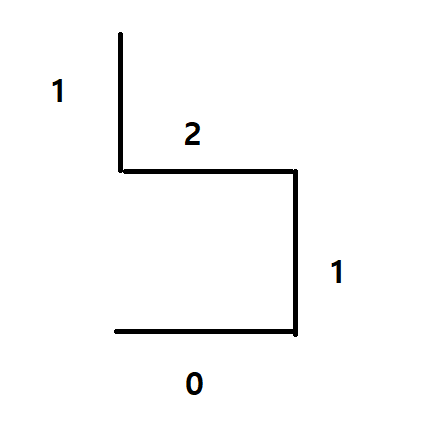
가장 중요한 부분입니다. 이전에는 [0,1] 방향으로 이동했습니다.
이때 전체 방향에 +1 를 해주면 [1,2] 가 됩니다. 하지만 이때 역순으로 이동해줘야합니다. 이후 방향은 [0,1,2,1] 이 됩니다.

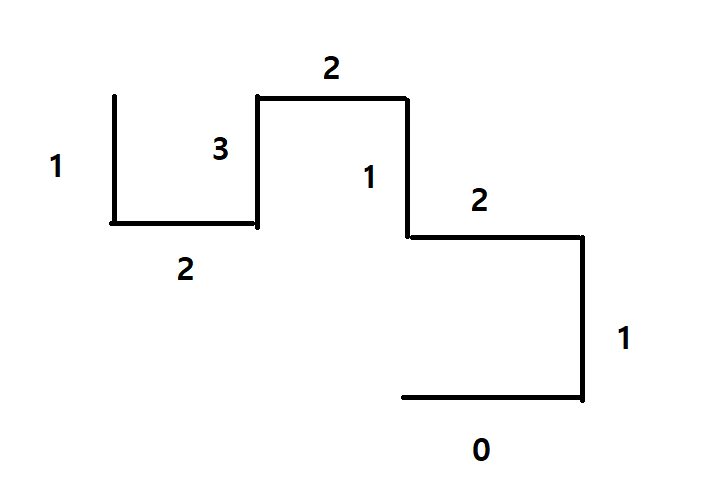
[0,1,2,1] 에서 전체 1을 더해주면 [1,2,3,2] 가 되고 이를 역순으로 하면 [2,3,2,1] 이 됩니다. 따라서 전체 이동방향은 [0,1,2,1,2,3,2,1] 이 됩니다.

📌 1 세대

본문에 적힌 코드는 1세대를 기준으로 풀이한 코드입니다. 0 세대보다 풀이가 더 복잡합니다.

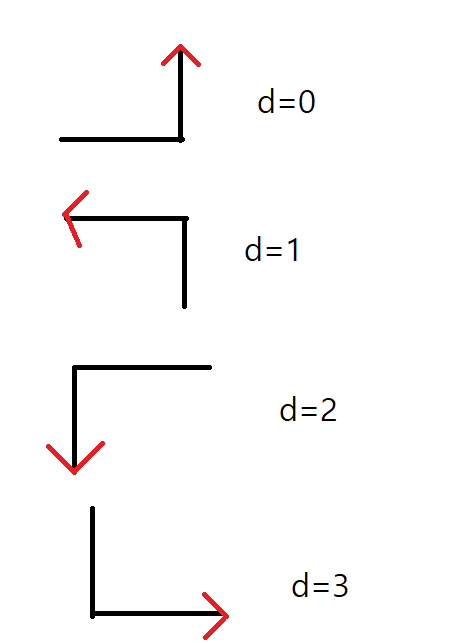
1세대로 만들 수 있는 그림은 총 4가지 입니다. 이때 주의해야할점은 방향도 설정해주어야 합니다.

제일 위의 그림은 오른쪽-위 로 가지만 아래-왼쪽으로 가도 똑같은 모양이 만들어 지기때문입니다.

시계방향으로 돌리면 $d$ 는 감소하는 방향으로 흐릅니다. $d$ 가 0일때는 3이 됩니다.

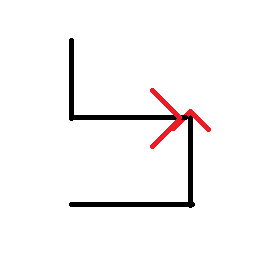
2세대를 만들때 문제가 발생합니다. $d$ 가 0 인 모양을 시계방향으로 회전시킨 $d$ 가 3인 그림을 붙이면
방향이 잘못되게 나옵니다. 아래-오른쪽이 아니라 왼쪽-위가 맞습니다.

for k in range(-1, -3, -1):
    x -= direction[d][k][0] ; y -= direction[d][k][1]
    graph[x][y] = 1

따라서 아래 오른쪽 을 오른쪽 아래로 역방향으로 한뒤 , 방향도 반대로 해주어서 왼쪽 위 로 설정해주었습니다.

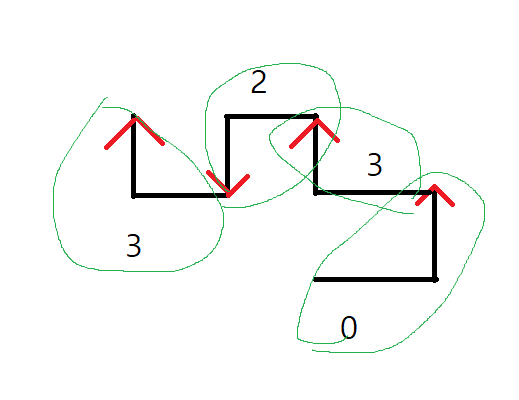
[0,3] 까지 만들었습니다. 이전에 찾은 규칙을 적용해봅시다. 일단 전체 1을 빼주었습니다.
그럼 [3,2] 가 만들어 집니다. 음수가 되면 3 으로 대채해줍니다. 이후 역순으로 바꿔줍니다. [2,3] 이 됩니다. 따라서 전체 그림은 [0,3,2,3] 이 됩니다.

이제 전체 코드를 살펴봅시다.

graph=[ [0]*101 for _ in range(101) ]

dx=[0,-1,0,1]
dy=[1,0,-1,0]
direction=[ [(0,1) , (-1,0)] , [(-1,0) , (0,-1)] , [(0,-1) , (1,0)] , [(1,0) , (0,1)] ]
N=int(input())

그래프를 설정해주고 dx 와 dy 는 세대가 0 일때 사용했습니다. 이후 세대가 1이상일때는 direction 을 사용했습니다. $N$ 을 입력받습니다.

for i in range(N):
    y,x,d,g=MI() #입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다.
    if g==0:
        graph[x][y]=graph[x+dx[d]][y+dy[d]]=1

$N$ 번동안 좌표와 방향과 세대를 입력받습니다. 세대가 0 일때는 그냥 dx,dy 를 사용해서 그래프에 1 을 넣어줍니다. 참고로 입력의 $x$ , $y$ 좌표는 반대로 주어지니 조심해야합니다.

Q=[]
while g:
    if not Q:
        graph[x][y]=1
        for j in range(2):
            x+=direction[d][j][0] ; y+=direction[d][j][1]
            graph[x][y]=1

        if d==0:
            Q.append([3,1]) # 두번재 값인 0 은 정방향 , 1은 역방향.
        else:
            Q.append([d-1,1])
        g-=1

$g$ 가 0일때까지 $while$ 문을 사용하여 반복합니다. 만약에 1 세대를 만들때는 direction 을 사용해서 x,y 좌표값을 이동시키면서 그래프를 1 로 채워줍니다. 이후 d 의 방향은 -1 을 해주고 처음에는 정방향으로 이동했으니 역방향으로 이동하기 위해서 $Q$ 배열에 $d$ 값과 역방향을 의미하는 1 을 넣습니다.

P=[]
for j in range(1,len(Q)+1):
    d=Q[-j][0]
    if Q[-j][1]==0: # 정방향이라면.
        if d==0:
            P.append([3,1])
        else:
            P.append([d-1,1])
        for k in range(2):
            x+=direction[d][k][0] ; y+=direction[d][k][1]
            graph[x][y]=1
    else: # 역방향이라면
        if d == 0:
            P.append([3, 0])
        else:
            P.append([d - 1, 0])
        for k in range(-1,-3,-1):
            x -= direction[d][k][0] ; y -= direction[d][k][1]
            graph[x][y] = 1
for a,b in P:
    Q.append([a,b])
g-=1

$Q$ 에 배열이 있을때 , 즉 2세대 이상을 만들려고 할때 입니다.
반복문을 통해 $Q$ 를 역순으로 인덱스를 가져옵니다. $d$ 변수에 방향을 가져오고 정방향일때는 임시의 $P$ 배열에 다음에 사용할 방향 $d$ 와 역방향값인 1 을 넣습니다.
그리고 총 2번동안 좌표를 이동해주면서 그래프 값을 1 로 설정해줍니다.
이후 이동했을때의 정보를 담은 $P$ 배열의 원소를 $Q$ 에 다시 집어넣어줍니다.

for k in range(-1, -3, -1):
    x -= direction[d][k][0] ; y -= direction[d][k][1]
    graph[x][y] = 1

역방향일때는 방향을 반대로 하기 위해서 좌표에 값을 빼주고 , 순서도 역순으로 하기 위해 인덱스도 뒤에서 탐색해줍니다. 이전에 아래-오른쪽을 왼쪽-위로 해준것처럼 해주었습니다.

total = 0
for i in range(1,101):
    for j in range(1,101):
        if [graph[i-1][j-1],graph[i-1][j],graph[i][j-1],graph[i][j]]==[1,1,1,1]:
            total+=1
print(total)

이제 마지막 부분입니다. 그래의 꼭짓점은 다 적어놨습니다.

우리가 원하는 것은 '정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 것의 개수를 출력한다.' 이므로 상하좌우 그래프의 값이 모두 1일때 total 변수에 1 을 추가해주고 total 변수를 출력해주면 답이됩니다.

1세대를 기준으로 해서 풀수도있지만 0 세대를 기준으로 풀 수 있습니다.