백준 20924 : 트리의 기둥과 가지 (Python)

본문 링크

import sys
input=sys.stdin.readline
sys.setrecursionlimit(10**9)

N,R=map(int,input().split())
Tree=[ [] for _ in range(N+1) ]


def DFS(start,count):
    global First,New_start,leaf_check
    check=[]
    visit[start]=True
    for i,j in Tree[start]:
        if not visit[i]:
            check.append([i,j])
            leaf_check+=j

    if len(check)>=2:
        First=count ; New_start=start
        return
    else:
        if check:
            DFS(check[0][0] , count+check[0][1])

def DFS2(start,count):
    global ans
    visit[start]=True
    for i,j in Tree[start]:
        if not visit[i]:
            ans=max(ans,count+j)
            DFS2(i,count+j)


for i in range(N-1):
    a,b,d=map(int,input().split())
    Tree[a].append([b,d])
    Tree[b].append([a,d])

visit=[False]*(N+1)
First=0 ; New_start=-1 ; ans=0 ; leaf_check=0

DFS(R,0)

DFS2(New_start,0)

if New_start==-1:
    print(leaf_check,ans)
else:
    print(First,ans)

📌 어떻게 접근할 것인가?

이 문제는 문제를 잘 읽어보야아한다. 트리에 특수한 개념을 적용시켰다.

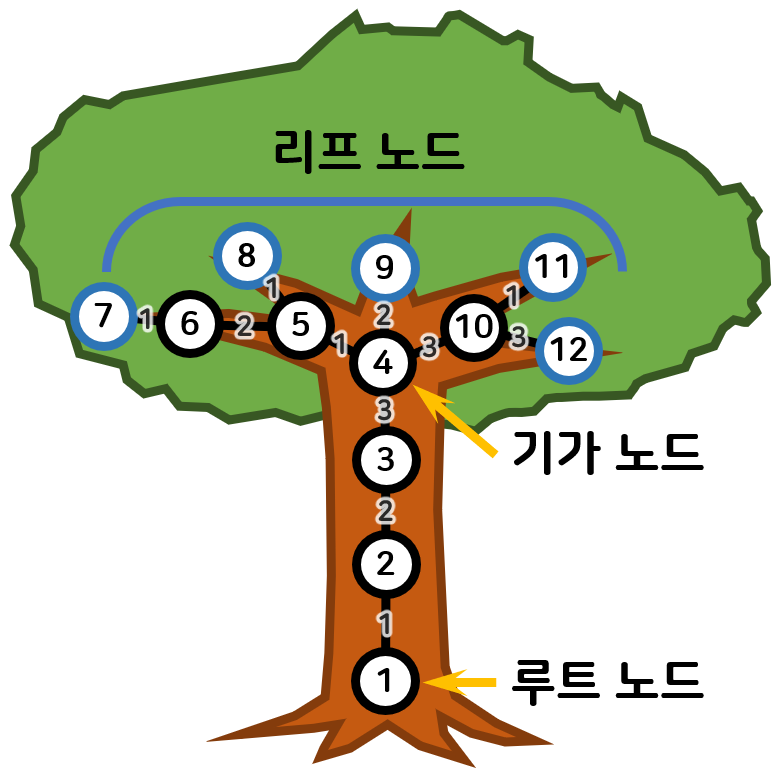
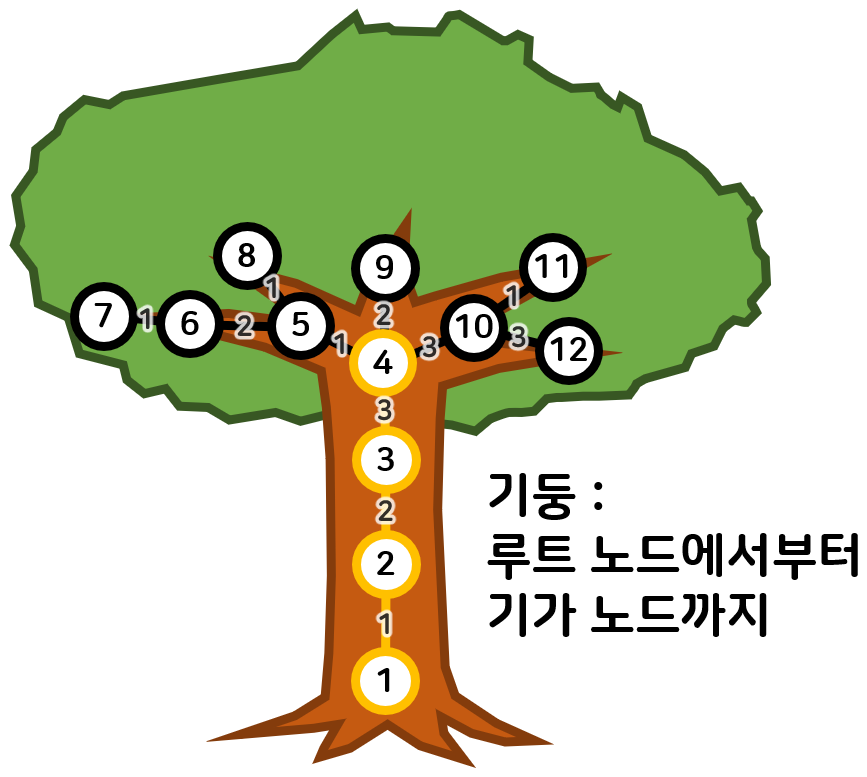
먼저 기가노트에 대해 알아보자.
기가노트란 처음으로 자식 노드가 $2$ 개 이상인 노드를 말한다.
따라서 기가노드는 $4$ 가 된다.

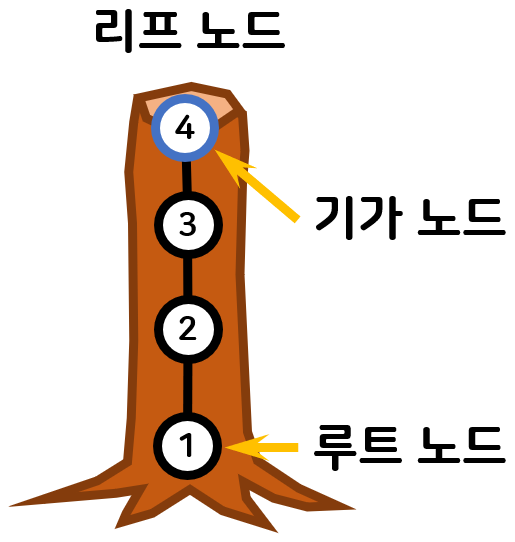
이때 주의해야할 점은 기가노드가 존재하지 않을때 , 즉 한방향으로만 트리가 존재할때
리프노드를 기가노드로 정의힌다.

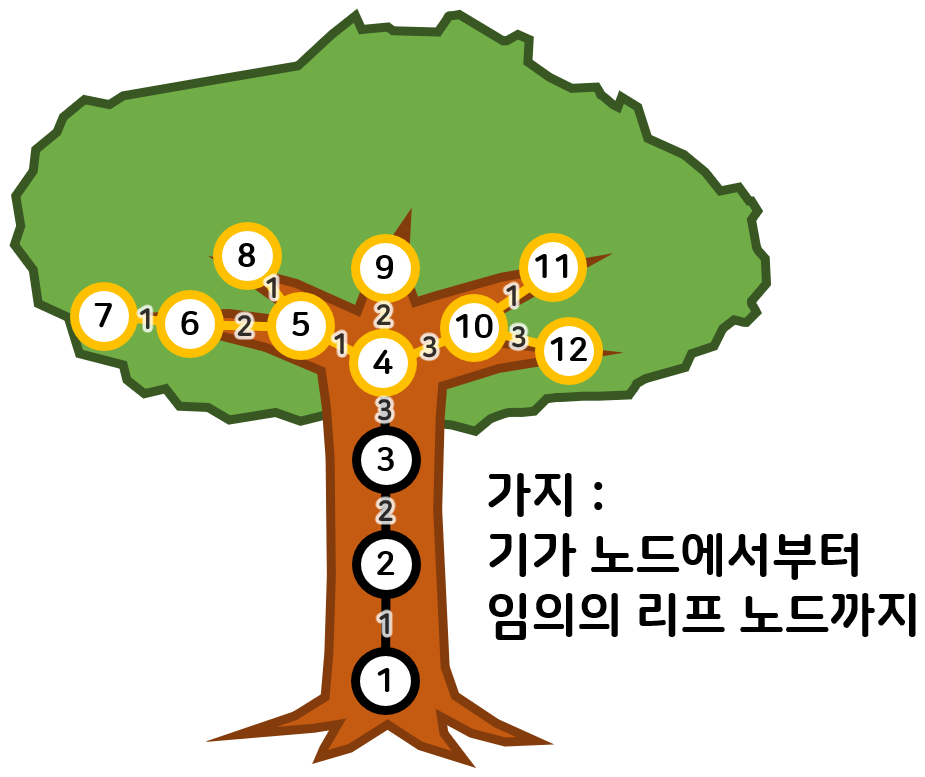
다음으로 구해야할 것은 트리의 가장 긴 가지의 길이다.

다만 가지는 이전에 구한 기가 노드부터 리프노드까지의 길이를 의미한다.
즉 $4$ 부터 리프노드까지 가중치를 계산해서 가장 거리가 먼 4-10-12 경로가 총 $6$ 으로 가장 길다.

따라서 $1$(루트노드)부터 $4$(기가노드) 까지의 거리 $6$(1+2+3) 과 기가노드부터 리프노드까지의 거리 $6$ 이 답이 된다.

✅ Code

먼저 트리는 양방향이기 때문에 원소를 $2$ 번 넣어준다. 이때 가중치도 함께 넣어준다.

Tree=[ [] for _ in range(N+1) ]
for i in range(N-1):
    a,b,d=map(int,input().split())
    Tree[a].append([b,d])
    Tree[b].append([a,d])

이후 변수와 리스트를 선언해준다.

visit=[False]*(N+1)
First=0 ; New_start=-1 ; ans=0 ; leaf_check=0

visit 는 방문 체크 배열이고 First 는 기가노드까지의 거리 , New_start 는 기가노드의 위치를 의미한다. ans 은 기가노드부터 리프노드까지의 거리이고 , leaf_check 는 기가노드가 존재하지 않을때 거리를 저장할 변수이다.

총 $2$ 개의 함수를 만들었다. 첫번째 함수부터 알아보자.

def DFS(start,count):
    global First,New_start,leaf_check
    check=[]
    visit[start]=True
    for i,j in Tree[start]:
        if not visit[i]:
            check.append([i,j])
            leaf_check+=j

    if len(check)>=2:
        First=count ; New_start=start
        return
    else:
        if check:
            DFS(check[0][0] , count+check[0][1])

DFS(R,0)

함수의 start 는 트리 값을 의미하고 count 는 가중치를 의미한다.
만약 방문하지 않은 지점이 있으면 check 배열에 위치와 가중치를 임시적으로 저장한다.
만약 check 배열의 길이가 2 이상이라면 , 즉 자식노드가 2개 이상이라면 그 지점은 기가노드가 되므로 가중치와 위치를 저장하고 return 을 한다. 만약 그렇지 않을 경우 재귀함수를 실행시킨다.

이때 모든 트리가 자식노드가 1개일수도있으니(리프노드 제외) leaf_check 에다가 가중치를 매번 더해준다.

def DFS2(start,count):
    global ans
    visit[start]=True
    for i,j in Tree[start]:
        if not visit[i]:
            ans=max(ans,count+j)
            DFS2(i,count+j)
       
DFS2(New_start,0)

다음으로 2번째 함수이다.
다만 두번째 함수를 호출할때는 시작점이 $R$ 이 아니라 이전에 구한 기가노트 (New_start) 를 기준으로 잡는다. 또한 visit 배열은 방문초기화를 하지않고 그대로 쓴다.

ans 변수를 선언해서 매번 기가 노드부터 리프노드까지의 거리를 갱신해준다.

if New_start==-1:
    print(leaf_check,ans)
else:
    print(First,ans)

따라서 다음과 같이 출력하면 정답이다.

문제의 내용이 길고 복잡해보지만 직접 코드를 작성하면 어려운 부분은 없기 때문에
천천히 읽어보고 이해하면서 문제를 풀어보기를 바란다.

✅ 여담

개인적으로 제일 어려워 하는 알고리즘이 재귀와 트리인데 스스로 풀어서 한번에 AC 를 받았다.
트리를 공부한지 일주일이 넘은거같은데 실력이 늘어나는거 같아서 기쁘다.

문제를 풀다가 어려워서 쉽게 포기하지말고 끝까지 노력해서 시도해보자. 중요한건 꺾이지 않는 마음이다.