백준 2263 : 트리의 순회 (Python)

본문 링크

import sys
input=sys.stdin.readline
sys.setrecursionlimit(10**9)

def DFS(inorder_start,inorder_end,postorder_start,postorder_end):

    if (inorder_start>inorder_end) or (postorder_start>postorder_end):
        return

    root=postorder[postorder_end]
    size=dp[root]-inorder_start
    ans.append(root)

    DFS(inorder_start,dp[root]-1 , postorder_start , postorder_start+size-1)
    DFS(dp[root]+1 , inorder_end , postorder_start+size , postorder_end-1)



N=int(input())
dp=[-1]*(N+1)

inorder=[-1]+list(map(int,input().split()))
postorder=[-1]+ list(map(int,input().split()))

for i in range(N+1):
    dp[inorder[i]]=i
ans=[]
DFS(1,N,1,N)
print(*ans)

📌 어떻게 접근할 것인가?

문제는 인오더와 포스트오더가 주어졌을 때, 프리오더를 구하는 것이다.

블로그 - 이 분의 블로그를 참고하였는데 정말 깔끔하게 잘 설명해주셨다.

함수의 개형은 다음과 같다.

DFS(중위순회 범위, 후위순회 범위):

	루트출력();
	DFS(중위순회의 L부분 범위, 후위순회의 L부분 범위);
    DFS(중위순회의 R부분 범위, 후위순회의 R부분 범위);

이때 중요한 것은 후위순회의 가장 끝부분은 루트라는 점이다.
위 순회를 안다면 루트의 값 알아낼 수 있고
중위 순회에서 그 루트 값 위치에 따라 L부분과 R부분으로 쪼갤 수 있습니다.
이를 재귀적으로 탐색하면 프리오더를 구할 수 있습니다.

예를 들어보겠습니다.

• 중위 순회 결과 : DBAECFG
  후위 순회 결과 : DBEGFCA

이때 루트 값은 후위 순회의 마지막 값인 'A'가 됩니다.
(후위 순회의 구조 - L/R/Root)

그리고 중위 순회에서 루트 값인 'A'를 기준으로 Left (DB)와 Right (ECFG)로 나눠지게 됩니다.
(중위 순회의 구조 - L/Root/R )

이 정보를 통해 후위 순회도 L과 R으로 나눌 수 있습니다.
중위 순회 L부분 개수 == 후위 순회 L부분 개수, 중위 순회 R부분 개수 == 후위 순회 R부분 개수 가 성립하기 때문입니다.

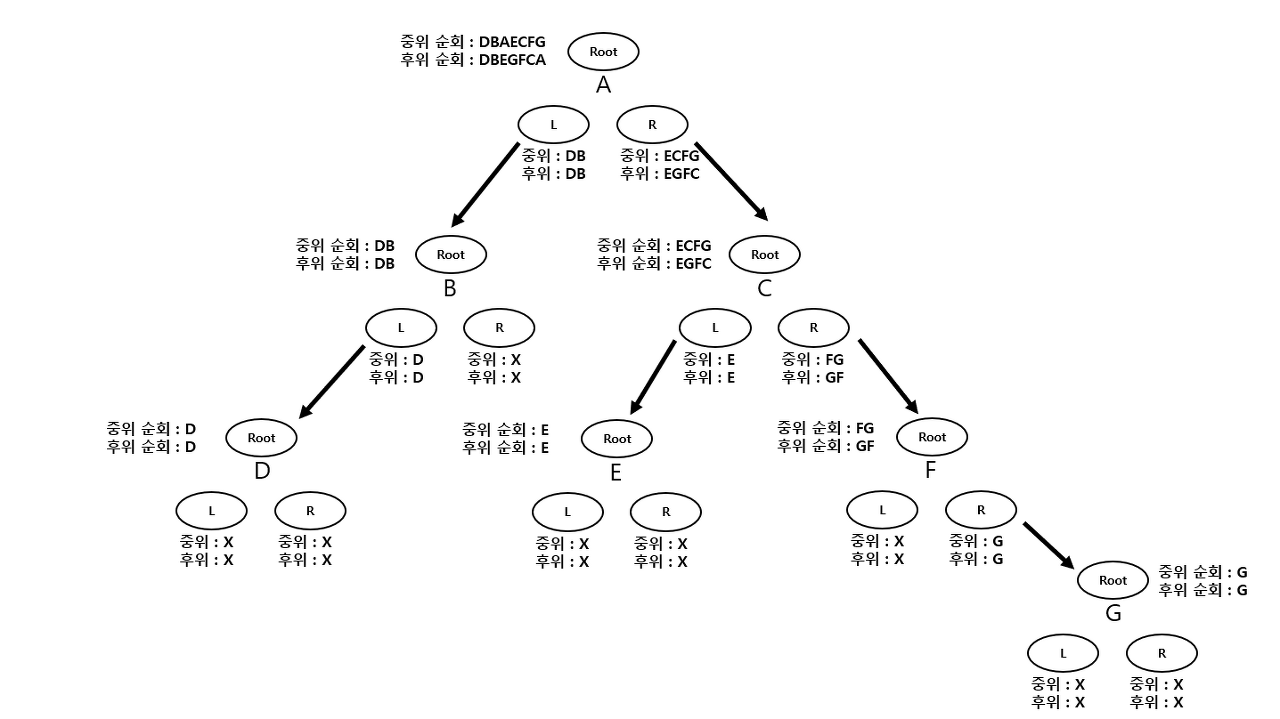
그림으로 설명하면 다음과 같습니다.