유니온 파인드 - Union Find

📌 유니온 파인드 - $Union$ $Find$

또는 상호 베타적 집합 , 분리집합 , $Disjoint$ $Set$ 이라고 부르는 자료구조 입니다.

유니온 파인드의 목적은 두 노드가 같은 집합에 속하는가? 를 찾는 것입니다.

그리고 총 2가지 연산을 수행합니다.

• Union : 노드를 합칩니다.
• Find : 서로다른 노드가 같은 집합인지 판별합니다.

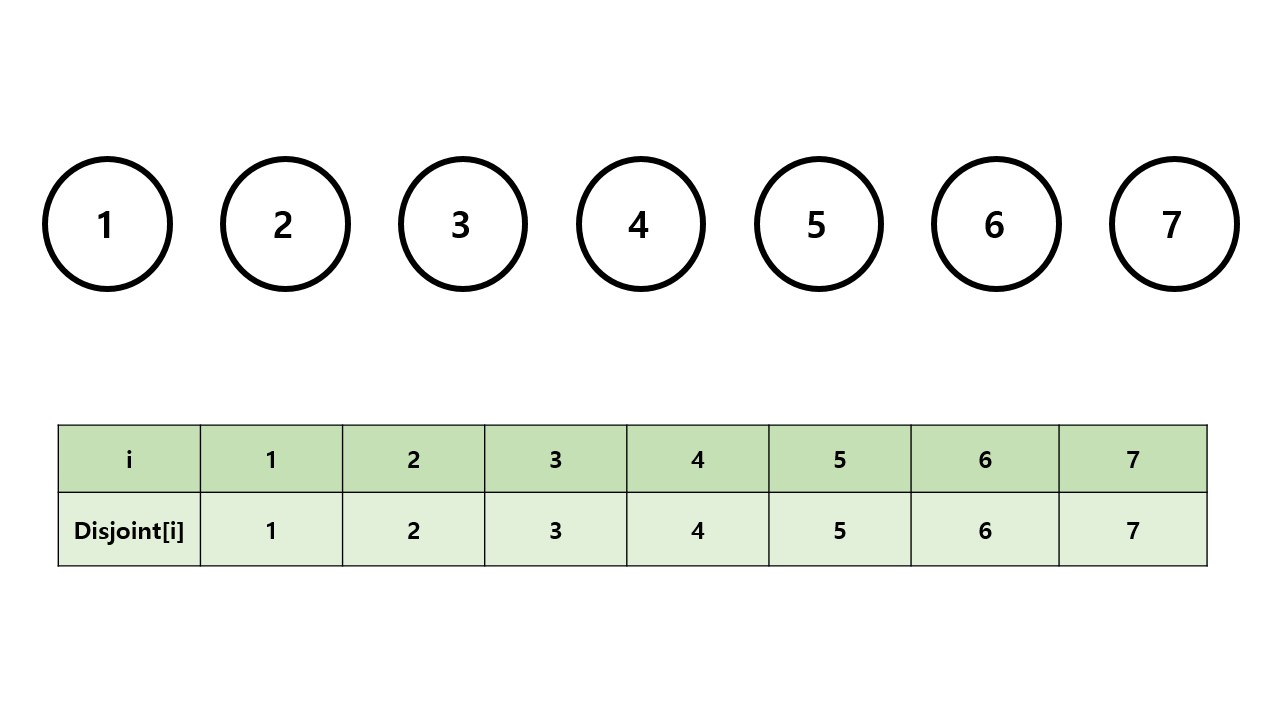
이런 단절된 노드가 있다고 해봅시다.

Disjoint=[0]*(N+1)

for i in range(1,N+1):
    Disjoint[i]=i

일단 유니온 파인드를 사용하기 이전의 노드들의 조상은 자기자신을 가르키게 합니다.

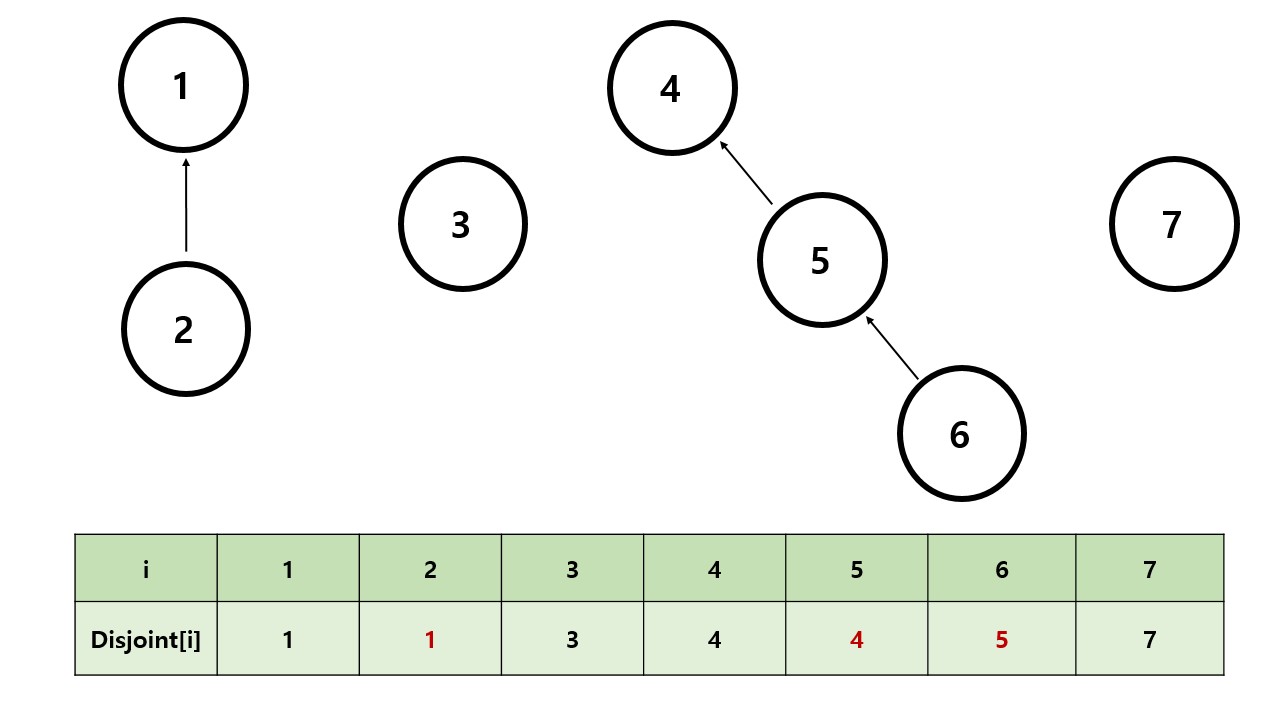
만약 노드들을 합치고 싶다면 , $Disjoint[i]$ 값을 부모노드의 번호로 바꾸어줍니다.

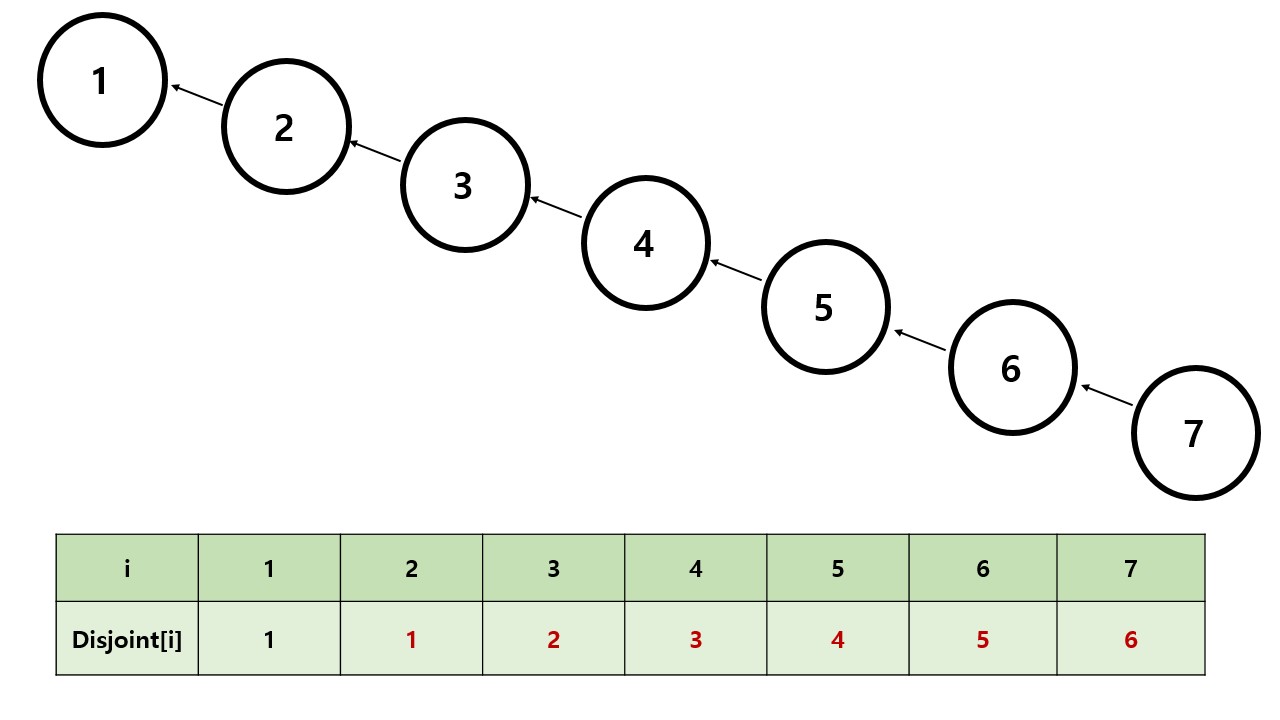
하지만 이렇게 처리할시 이런 그래프가 주어졌을때 $7$ 번 노드에서 최상위 부모 노드를 찾을때 $O(N)$ 의 시간복잡도가 필요합니다.

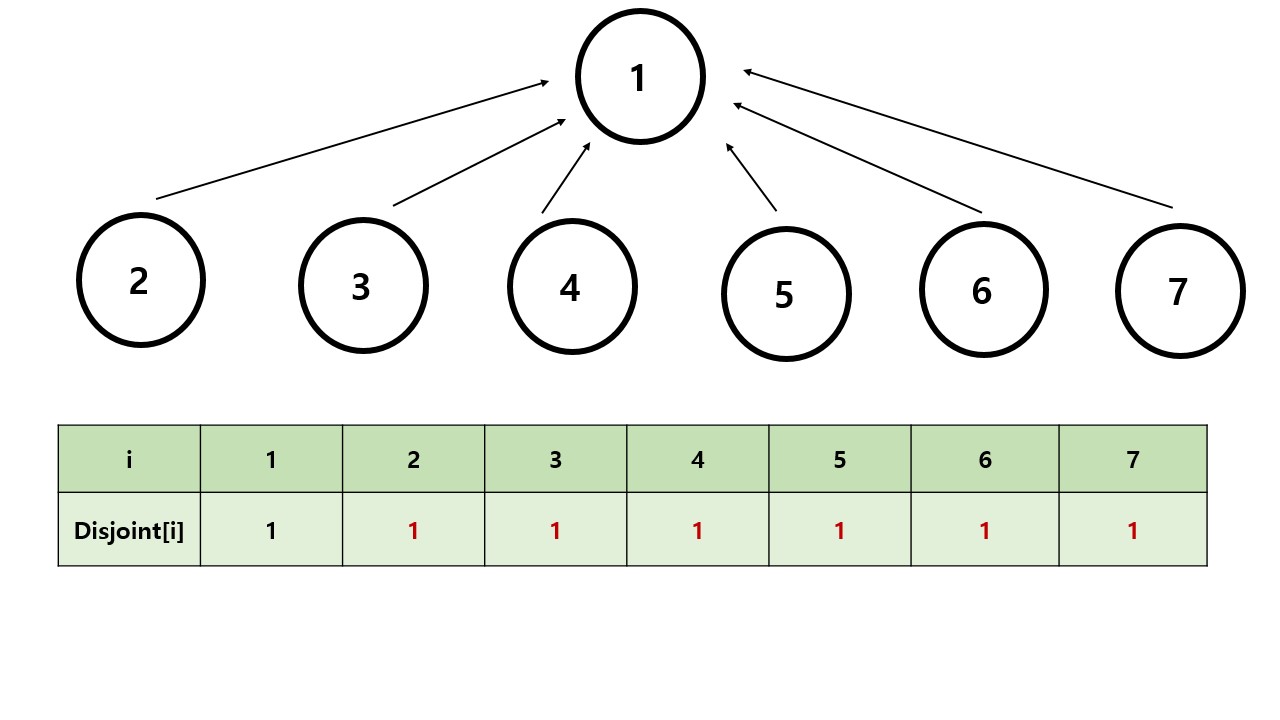
이때 최적화를 위해서 모든 $Disjoint[i]$ 값은 부모노드가 아니라 최상위 부모노드를 가르키게 합니다.

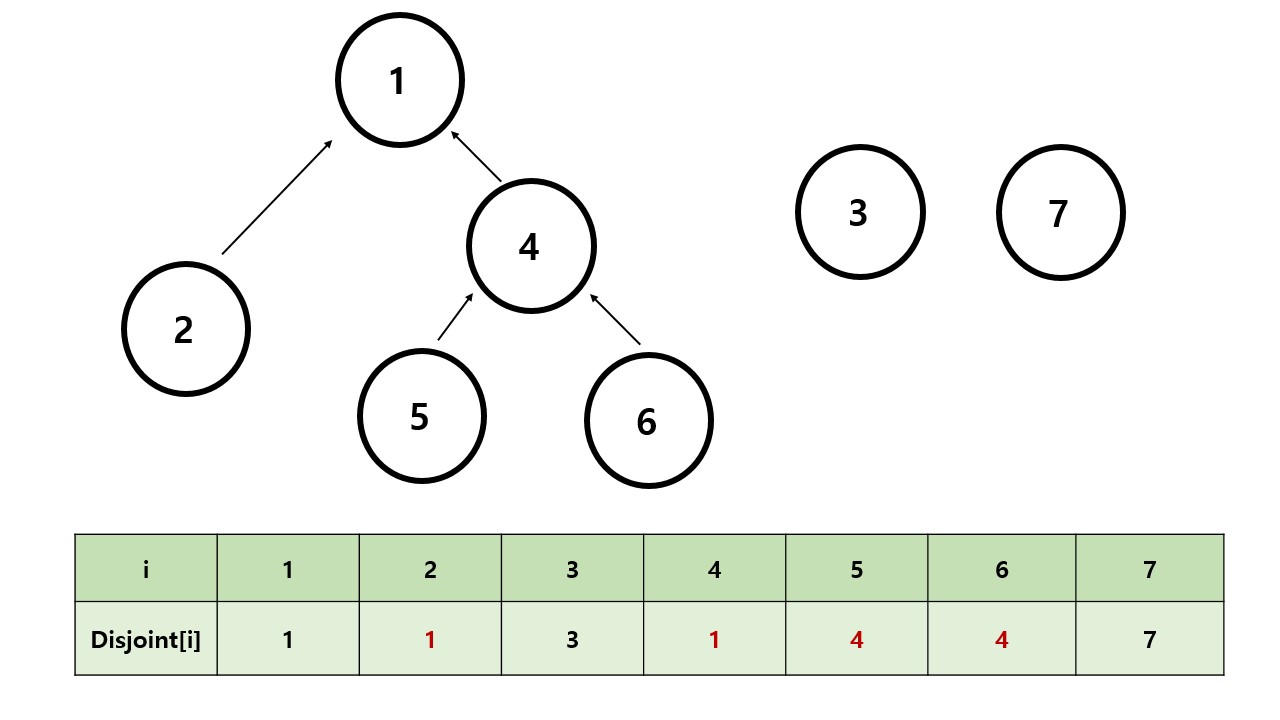
따라서 두 노드를 합치는 것도 위와 같이 최적화가 가능합니다.

이제 파이썬 코드를 직접 보겠습니다.

📌 전체 코드

import sys
input=sys.stdin.readline
sys.setrecursionlimit(10**9)

def Find(x):

    if Disjoint[x]!=x:
        Disjoint[x]=Find(Disjoint[x])
    return Disjoint[x]

def Union(A,B):

    A=Find(A)
    B=Find(B)

    if A<B:
        Disjoint[B]=A #더 작은 값을 넣어주어야함.
    else:
        Disjoint[A]=B


N,M=map(int,input().split())
Disjoint=[0]*(N+1)

for i in range(1,N+1):
    Disjoint[i]=i



for i in range(M):

    print(Disjoint)
    K,A,B=map(int,input().split())
    if K==0:
        Union(A,B)
    else:
        if Find(A)==Find(B):
            print("YES")
        else:
            print("NO")

✅ Code 탐색

집합의 표현 문제의 코드입니다.

일단 코드를 하나하나 보겠습니다.

Disjoint=[0]*(N+1)

for i in range(1,N+1):
    Disjoint[i]=i

유니온 파인드를 하기 전에 해야하는 부분입니다. 모든 노드들은 자기자신을 먼저 가르키도록 합니다.

def Find(x):
    if Disjoint[x]!=x:
        Disjoint[x]=Find(Disjoint[x])
    return Disjoint[x]

두 노드가 같은지 찾는 $Find$ 함수 입니다. 만약 Disjoint[x]!=x 라면 , 즉 찾고자 하는 값과 일치하지 않다면 Disjoint[x]=Find(Disjoint[x]) 을 실행합니다. 이는 아까 설명한 것처럼 최적화를 하는 부분이며 , Find 로 노드를 찾을때마다 최상위 노드를 갱신해주는 과정을 의미합니다.

그리고 자식노드는 부모노드의 번호를 저장하기 위해서 return Disjoint[x] 를 수행합니다.

def Union(A,B):

    A=Find(A)
    B=Find(B)

    if A<B:
        Disjoint[B]=A #더 작은 값을 넣어주어야함.
    else:
        Disjoint[A]=B

다음은 합치는 과정입니다. 두 노드의 최상위 노드를 A=Find(A) , B=find(B) 를 통해 찾아주고

번호가 더 작은 값을 넣어줍니다.

if Find(A)==Find(B):
	print("YES")
else:
    print("NO")

두 노드가 같은 집합에 속해있는지 판별하는 것은 위처럼 판별하면 됩니다.
즉 두 노드의 최상위 노드가 일치한가? 를 통해 판별 가능합니다.

이상으로 여기까지 소개하겠습니다.