이분 탐색 - Binary Search

📌 이분탐색이란?

이분 탐색 - $Binary$ $Search$

❓ 배열에 특정 값이 어디에 있는가?

배열이 주어졌을때 원하는 값이 있는지 , 있다면 어디에 위치하는지 찾는 알고리즘 입니다.

만약 아래와 같은 배열이 있다고 해봅시다.

• $[5,2,7,6,9,4]$

여기서 4 라는 값은 한눈에 찾을 수 있습니다.

하지만 만약에 배열의 길이가 10만개 이상이고 모든 원소들이 무작위로 섞여있다면 어떻게 빠르게 찾을 수 있을까요?

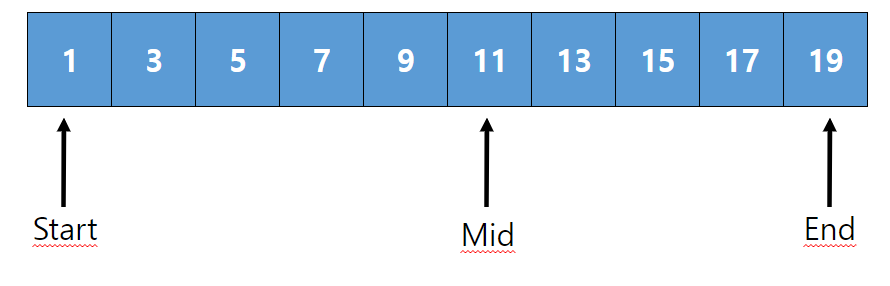
이분탐색을 통해 배열에서 7 이라는 값을 찾아보겠습니다.

먼저 배열의 Start 와 End 값을 잡아줍니다.
Start 는 배열의 시작점 , End 는 배열의 끝으로 잡아준뒤
Mid 값은 (Start+End)//2 값으로 잡아줍니다.

1부터 19까지 홀수가 있는 배열에서 중간값은 11 입니다.

중간값이 7보다 크기 때문에 왼쪽으로 이동하기 위하여 End=Mid-1 로 잡고 다시 Mid 값을 잡습니다.

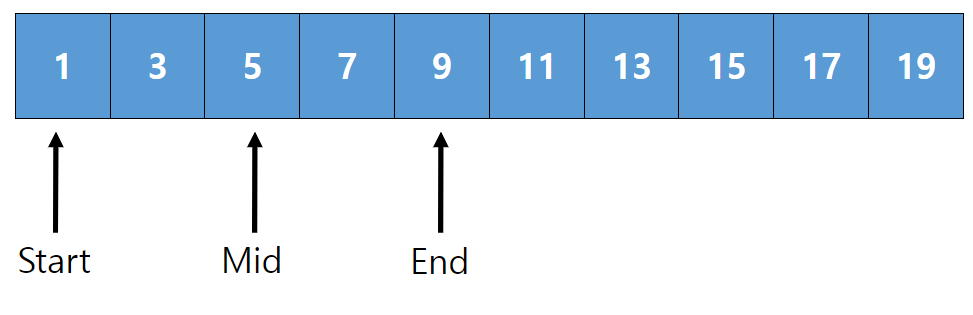
이번엔 Mid 값이 5가 되었습니다.

하지만 우리가 찾고자 하는 값이 7이기 때문에 Mid 값이 7보다 작으므로
오른쪽으로 이동하기 위하여 Start=Mid+1 로 잡아줍니다.

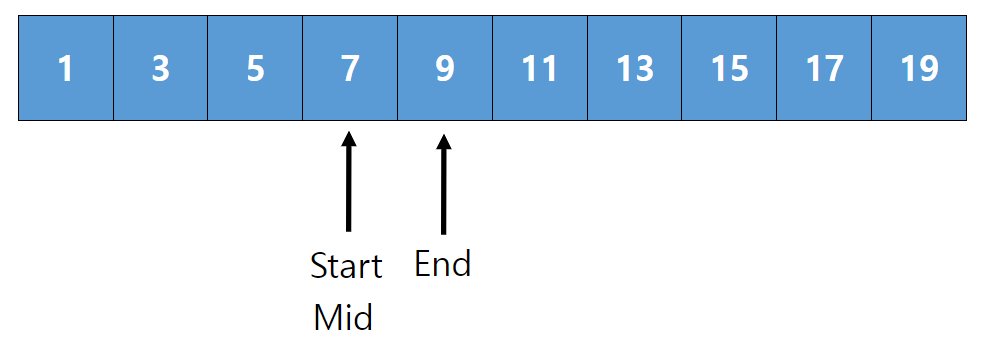
Start 의 인덱스는 3 , End 의 인덱스는 4 이므로
Mid=(3+4)//2=3 이므로 Start 와 값이 같습니다.

따라서 Mid 값이 우리가 찾고자 하는 값인 7과 같아지기 때문에
이분탐색이 종료됩니다.

📌 이분탐색 코드

start=0 ; end = N

while start<=end:
	
    mid=(start+end)//2
    
    if mid>K:
    	end=mid-1
    
    elif mid<K:
    	start=mid+1
        
    elif mid==K:
    	break

시작값과 끝값을 정해주고 중간값을 정해준뒤 특정값 $K$ 보다 큰지 작은지에 따라
시작값과 끝값을 변경해주면 됩니다.

만약 중간값이 $K$ 값과 일치하다면 이분탐색은 종료됩니다.

📌 이분탐색 전제조건

먼저 이분탐색을 사용하기 위해서는 다음과 같은 조건을 만족해야 합니다.

• 배열은 정렬 되어있어야한다. ( 오름차순 , 내림차순 어떤식으로든 )
• 찾고자 하는 값이 존재해야한다.

따라서 배열에 특정한 값을 이분탐색으로 찾고자 할때는
문제에서 배열을 정렬하지 말라고 말하지 않는 한 정렬을 해줘야 합니다.

📌 이분탐색 시간 복잡도

이분탐색은 총 $O(log N)$ 의 시작복잡도를 가집니다.

따라서 배열의 길이가 10만개 이상일때 원하는 찾을 찾기 위해서 사용하면
시간을 크게 단축 시킬 수 있습니다.

✅ 이분탐색 활용

이분탐색은 배열의 특정 값을 찾을 떄 사용할 수도 있지만

"어떤 수를 만족하는 K 가 존재하는가?" 라는 접근으로 사용할 수도 있습니다.

대표적인 문제로는 2805번 :나무 자르기 이런 문제가 있습니다.

특정 조건을 만족하는 수의 최대값&최소값을 찾을때 이분탐색을 통해서
$O(log N)$의 시간복잡도로 만족하는 값을 찾을 수 있습니다.

또한 이분탐색의 Start 값과 End 값 그리고 Mid 값은 배열의 인덱스로도 활용할 수 있습니다.

✅ 이분탐색은 언제 써야하는가?

보통 이분탐색을 써야한다고 생각할 때는 총 2가지가 있습니다.

• 주어지는 수의 범위가 너무 커서 $O(N)$ 으로 탐색할 수 없을 때
• 특정 값을 만족하는 수의 최대값과 최소값을 찾을 때

문제에서 주어지는 범위가 $O(N)$ 으로 탐색하기에는 터무니없이 크면
보통 이분탐색을 사용해서 시간단축을 합니다.

이외에도 이분탐색은 다양한 방법으로 사용할 수 있습니다. 이는 문제를 많이 풀어봄으로써 감각적으로 익히는게 제일 좋습니다.

누적합 처럼 간단한 알고리즘이지만 활용도는 매우 높기 때문에 적절하게 사용한다면 코드의 속도를 크게 단축시킬 수 있습니다.

이분탐색 문제집 - 이 문제집을 통해서 이분탐색에 대한 감각을 익히시는것을 추천드립니다.

이분탐색 코드 자체는 구현이 쉬우나 어떻게 활용할 것인지 , 무엇에 대한 값을 찾을것인지 , 시작값과 끝값 그리고 중간값을 어떻게 잡을지 생각해야합니다.