누적합 - Prefix sum

📌누적합 알고리즘 이란?

누적합 알고리즘 - $Prefix$ $sum$

❓ i~j 번째까지 배열의 총 합은 얼마인가?

문제에서 특정한 배열이 주어졌을때 특정 구간의 연속한 값들의 합을 빠르게 구하는 알고리즘 입니다.

예시를 들어보겠습니다.

• $[1,2,3,4,5]$

이라는 배열이 있을때 누적합 배열을 만들면

• $[1,3,6,10,15]$

라는 배열이 만들어 졌습니다.

누적합 배열을 응용하면 i~j 번째까지 연속한 값들의 합을 빠르게 구할 수 있습니다.

예시로 모든 배열의 합은 누적합 배열의 마지막 값을 의미하며

1부터 4까지의 합은 누적합 배열의 10을 의미합니다.

2부터 5까지의 합은 15-1=14로 시작점 끝점 모두 변경가능합니다.

📌 1차원 누적합 배열 Code

L=list(map(int,input().split()))

dp=[0]*(N+1)
for i in range(1 , len(L)):
    dp[i]=dp[i-1]+L[i-1]

코드 자체는 아주 간단합니다. 리스트를 입력받고 누적합 배열 $dp$ 를 리스트 길이+1 만큼 만들어 줍니다.

이후 점화식은 다음과 같습니다.

• $dp[i] = dp[i-1]+L[i-1]$

리스트의 전체 누적합 배열을 만들려면 시간복잡도는 $O(N)$ 입니다.

만약 배열의 인덱스 start 부터 end 까지의 합을 구하고 싶다면

• $dp[end]-dp[start-1]$

을 출력하면 됩니다.

즉 누적합 배열을 한번 만들면 특정 구간의 연속합을 단 한번의 계산을 통해 구할 수 있습니다.

📌 2차원 누적합 배열

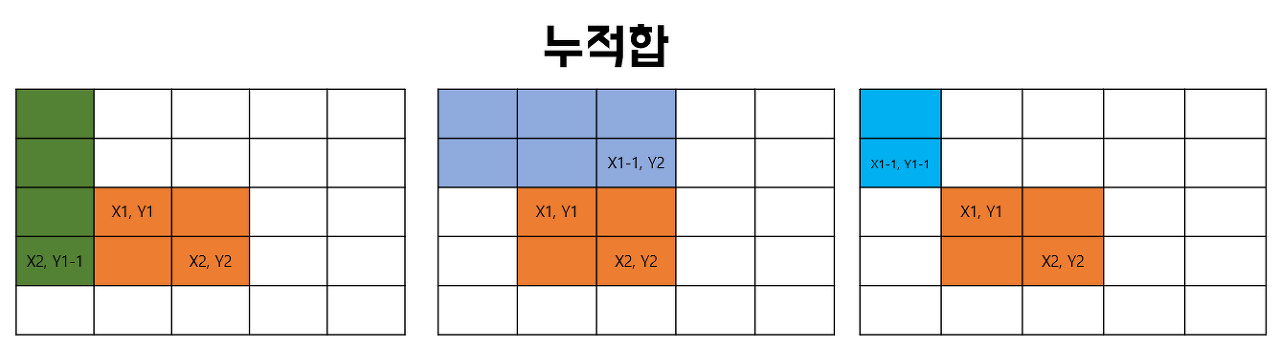
2차원 배열에서는 1차원 배열처럼 단순 누적합을 적용시키면 겹치는 부분이 생기기 때문에 다음과 같은 점화식을 적용시켜야 합니다

• $dp[i][j]=dp[i][j−1]+dp[i−1][j]−dp[i−1][j−1]+L[i][j]$

여기서 $dp$ 배열은 누적합 배열이고 $L$ 은 입력받은 리스트 값입니다.

따라서 $x1,y1$ 부터 $x2,y2$ 까지의 합은

• $dp[x2][y2]−dp[x1−1][y2]−dp[x2][y1−1]+dp[x1−1][y1−1]$

위와 같은 식이 성립됩니다.

✅ 활용방법

누적합 배열 자체는 구현이 되게 싶습니다. 하지만 누적합은 어떻게 활용할 것인가? 이 점이 가장 중요합니다.

우리가 누적합을 쓰는 이유는 시간복잡도를 줄이기 위해서 입니다.

누적합을 언제 쓸것이냐? 라는 질문에 대해서는 이렇게 대답하고 싶습니다.

특정한 구간의 연속된 수들의 합을 구할때 사용한다.

또는 특정 구간의 최대값 , 최소값을 구하는데 사용 할 수도 있고

배열의 구간중 합이 $K$ 인 이상인 구간 , 합이 $K$ 이면서 가장 짧은 것의 길이 등등
다양하게 응용할 수 있습니다.

하지만 연속된 구간이 아닌 배열의 합을 구할때는 누적합을 사용할 수 없습니다.

누적합은 어떻게 응용하느냐에 따라 활용도가 무궁무진하기 때문에 여러 문제를 풀어보시면서 감각을 익히는게 좋습니다.

누적합 문제집 - 이 문제집을 클릭해서 누적합에 대한 개념을 익히는 것을 추천드립니다.