최장 공통 부분 수열 - LCS

📌 LCS 알고리즘 이란?

최장 공통 부분 수열 $LCS$ - Longest Common Subsequenc

동적 계획법을 응용한 알고리즘 입니다.

❓ 어떤 임의의 수열이 주어졌을때 수열 모두의 가장 긴 공통 부분수열의 길이는 얼마인가?

예를들어보면

• ACAYKP
  CAPCAK

이라는 두 문자열 수열이 있습니다.
이때 가장 긴 공통 부분 수열은 A C A K 입니다.
따라서 $LCS$ 의 값은 4가 됩니다.

반면 ACAP 는 두번째 문자에 A 다음 P 가 없기때문에 $LCS$ 가 아닙니다.

부분수열이기 때문에 꼭 연속해야할 필요는 없고 부분수열 조건과 주어진 여러 수열의 공통 문자를 찾으면 됩니다.

🔑 2차원 DP 풀이법

import sys
input=sys.stdin.readline

a=input().rstrip()
b=input()

Breath=len(a)
High=len(b)

dp=[ [0]*(Breath+1) for i in range(High+1) ]

for i in range(High):
    for j in range(Breath):
        if a[j]==b[i]:
            dp[i][j]+=dp[i-1][j-1]+1
        else:
            dp[i][j]=max(dp[i][j-1],dp[i-1][j])

print(dp[-2][-2])

$dp$ 테이블의 행의 길이는 a문자열이 길이+1 , 열의 길이는 b문자열으 길이+1 로 잡아줍니다.

그리고 이중반복문을 사용하여서 문자열이 같다면
$dp[i][j]=dp[i-1][j-1]+1$ 로 하고
다르다면 $dp[i][[j]=max(dp[i][j-1] , dp[i-1][j])$ 로 잡아줍니다.

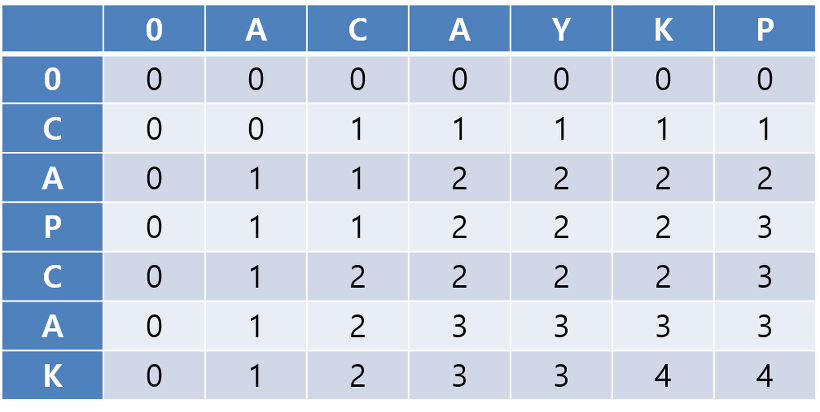
따라서 실제 dp 테이블 변화양상은 위의 사진과 같습니다.

🔑 1차원 DP 풀이법

import sys
input=sys.stdin.readline

a=input().rstrip()
b=input()

high=len(b)
breath=len(a)
dp=[0]*len(a)

for i in range(high):
    count=0
    for j in range(breath):
        if count<dp[j]:
            count=dp[j]
        elif b[i]==a[j]:
            dp[j]=count+1

print( max(dp) )

$LCS$ 는 1차원 배열로도 풀이 가능합니다.
이중반복문을 통해서 두가지 if 문을 사용합니다.
if count<dp[j] 가 의미하는 바는 지금까지 증가한 공통 부분수열의 길이중 매번 최대값을 count 에 저장한다는 뜻이고
elif b[i]==a[j] 는 a 와 b 문자열이 같을때 $dp$ 테이블에 현재까지 저장한 가장 긴 공통 부분수열의 길이+1을 저장한다는 뜻입니다.

🔑 LCS 문자 구하기

이번에는 $LCS$ 의 길이를 구하는 것이 아니라
실제 그때의 문자를 찾아보는 방법에 대해 알아보겠습니다.

a=[0]+ list(input().rstrip())
b=[0]+ list(input().rstrip())
high=len(a)
breath=len(b)
dp=[ [""]*breath for i in range(high) ]

string=""
for i in range(1,high):
    for j in range(1,breath):
        if a[i]==b[j]:
            dp[i][j]=dp[i-1][j-1]+a[i]
        else:
            if len(dp[i-1][j])>len(dp[i][j-1]):
                dp[i][j]=dp[i-1][j]
            else:
                dp[i][j]=dp[i][j-1]

print(len(dp[high-1][breath-1]))
print(dp[high-1][breath-1])

$dp$ 테이블 자체를 문자를 담을 수 있는 배열로 만들어 주면 됩니다.
따라서 두 문자가 같을때는 자료형 타입이 문자인 a[i] 를 $dp$ 테이블에 추가해줍니다.
만약 두 문자가 다를경우 $dp[i][j]$ 에는 $dp[i-1][j]$ 와 $dp[i][j-1]$ 문자열중 더 긴것을 저장해줍니다.

따라서 $dp$ 배열에 문자를 매번 저장하고 문자열 길이를 통해 비교한다면
$LCS$ 의 문자를 구할수 있습니다.

🔑 3개 문자열 LCS 구하기

이번에는 문자열이 3개가 주어졌을때 $LCS$ 를 구하는 방법에 대해 알아보겠습니다.

a=input()
b=input()
c=input()

x=len(a) ; y=len(b) ; z=len(c)

dp= [ [ [0]*(z+1) for i in range(y+1) ] for j in range(x+1)]
for i in range(1,x+1):
    for j in range(1,y+1):
        for k in range(1,z+1):
            if a[i-1]==b[j-1] and b[j-1]==c[k-1]:
                dp[i][j][k]+=dp[i-1][j-1][k-1]+1
            else:
                dp[i][j][k]=max(dp[i-1][j][k] , dp[i][j-1][k] , dp[i][j][k-1] )

print(max(max(max(dp))))

간단하게 생각해서 3개의 문자열을 모두 비교해주면 됩니다.

만약 3개의 문자가 모두 같을때
$dp[i][j][k]=dp[i-1[j-1][k-1]+1$ 를 저장하고
그렇지 않을 경우에는
$dp[i][j][k]=max(dp[i-1][j][k] , dp[i][j-1][k] , dp[i][j][k-1] )$ 값을 매번 저장해줍니다.

다만 이 방법은 $O(N^3)$ 풀이이고 문자열의 길이가 많이 커진다면 불가능한 방법입니다.

따라서 $N$ 이 아주 큰 경우에는 분할정복&히르쉬버그 를 통한 $LCS$ 를 구하는 방법도 존재합니다.

🔑Conclusion

$LCS$ 알고리즘이 무엇인지 , 2차원배열과 1차원 배열로 $LCS$ 를 구하는 법 , $LCS$ 문자열 구하는 방법 , 마지막으로 3개 문자열에 대한 $LCS$ 를 구하는 방법에 대해 알아보았습니다.
지금까지 설명한 내용만으로도 백준 실버~골드 문제는 충분히 풀 수 있습니다.
LCS 문제집 이 문제집을 통해 공부하시는걸 추천합니다.

다음에는 배낭문제에 대해 알아보겠습니다.