📌 Big O Notation
어떤 문제에 대해 다양한 접근법(알고리즘)이 있을때,
Big O Notation은 표준화된 방법으로 알고리즘의 성능을 분석하여 어떤 접근법이 더 좋은지 비교할 수 있도록 도와준다.
필요성
-
코드의 performance를 정확한 용어로 표현할 수 있다.
-
각 접근법의 장단점을 논의할 때 도움된다.
-
코드의 비효율적인 파트를 찾는데 도움된다.
-
면접에 자주 나오는 내용이다.
📚 사전 지식
"더 좋은 코드"의 기준은 무엇인가?
- 속도
- 메모리 사용량
- 가독성
속도가 빠르고, 메모리를 덜 차지하고, 가독성이 좋은 것이 좋은 코드라고 할 수 있고, 그 중에서도 속도와 메모리 사용량이 중요한 기준이 된다.
속도를 구하는 두가지 방법
- 시간 측정하기
- 연산의 갯수 세기
1. 시간 측정하기
Q. 숫자 n이 주어질 때 n보다 작은 숫자들의 합을 구하는 함수를 만드시오.
크게 2가지 방법이 있다.
- 반복문을 이용한 풀이
function addUpTo(n) {
let total = 0;
for(let i = 1; i <= n; i++){
total += i;
}
return total;
}- 수학 공식을 이용한 간단한 풀이
function addUpTo(n) {
return n * (n+1) / 2;
}각 방법의 실행 시간을 구해준다.
실행 시간 구하는 방법
처음 시간을 변수에 저장하고, 계산을 한 후에 종료 시간을 변수에 저장해서 둘의 차를 구한다.
performance.now() : 브라우저가 문서를 만든 시간을 알려줌.
let t1 = performance.now();
addUpTo(100000000);
let t2 = performance.now();
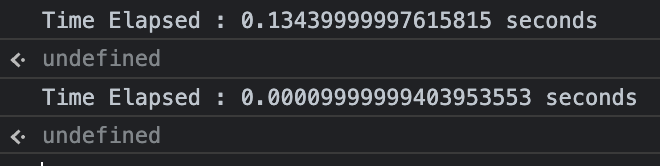
console.log(`Time Elapsed : ${(t2 - t1) / 1000} seconds`);결과
두 번째 방법의 실행 시간이 훨씬 적게 걸리는 것을 확인할 수 있다.
시간을 측정하는 방식의 문제점
- 기기마다 기록되는 시간이 다르다.
- 똑같은 기기가 다른 시간을 기록할 수도 있다.
- 매우 빠른 알고리즘의 경우 작은 차이를 측정하기 힘들다.
(속도 측정 정확도가 충분하지 않을 수 있다.)
결과적으로 시간을 측정하는 방식은
정확하지 않다!
시간을 이용하지 않고 속도를 알 수 있는 방법을 생각해보면, 컴퓨터가 처리해야 하는 연산의 갯수를 세는 방법이 있다.
시간은 항상 연산의 갯수에 달려있으므로 시간을 측정하는 것보다 연산의 갯수를 세는게 더 정확하다.
2. 연산의 갯수 세기
위의 문제에 똑같이 적용해보면,
첫 번째 풀이는 5n+2번의 연산(for loop와 그외 등등)이 이루어지고,
두 번째 풀이는 3번의 연산(곱셈,덧셈,나눗셈)이 이루어진다.
첫 번째 풀이는 n이 커질수록 연산의 갯수가 비례적으로 늘어나기 때문에 두 번째 풀이의 속도가 훨씬 빠를 것이라는 것을 알 수 있고, 이 방식이 시간을 이용하는 방식보다 더 정확하게 속도를 비교할 수 있는 방법이 된다.
따라서 Big O Notation에서는 시간이 아닌
연산의 갯수를 통해 속도와 메모리 사용량을 분석한다.
🤔 그래서 Big O Notation은 무엇인가?
입력값이 늘어날 수록 알고리즘의 실행 시간이 어떻게 변하는지를 설명하는 공식적인 방법이다.
-> 요약하자면 입력 크기와 실행 시간의 관계를 말함.(전반적인 추세)
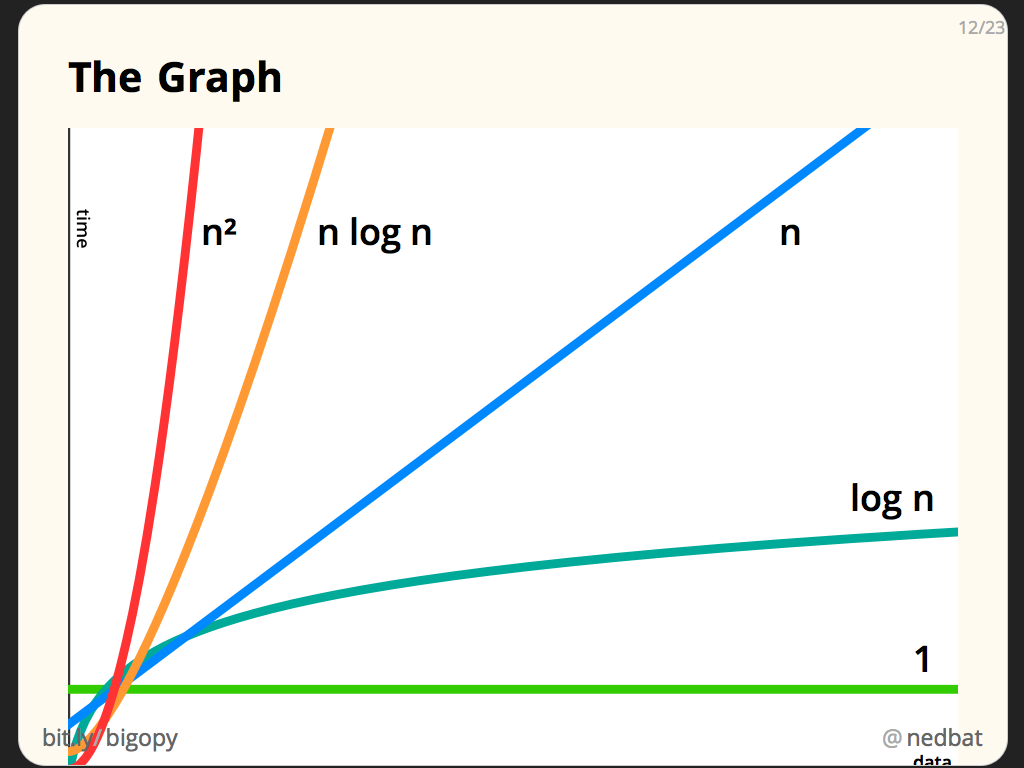
4가지 양상
n이 입력값이고 f(n)이 실행시간이라고 했을 때, f(n)은 크게 4가지 양상으로 나타날 수 있다.
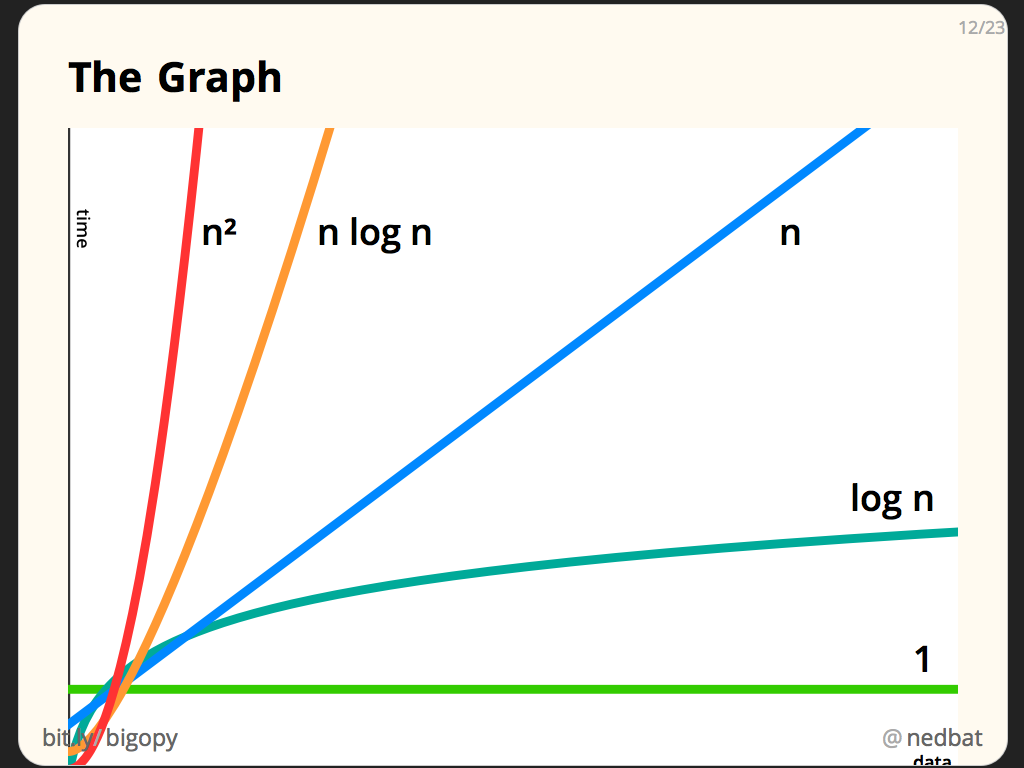
-
linear(선형 관계) : f(n) = n
입력값이 커짐에 따라 시간이 일정하게 늘어남.(위 예시의 방법1이 여기에 해당함)
Big O 표기 :O(n) -
quadratic(2차) : f(n) = n^2
입력값의 제곱만큼 시간이 늘어남.(ex.중첩 반복문)
Big O 표기 :O(n^2) -
constant(상수) : f(n) = 1
입력값이 커져도 시간에는 아무 영향이 없음.(위 예시의 방법2가 여기에 해당함)
Big O 표기 :O(1) -
Logarithm(로그) : f(n) = log n, f(n) = nlog n
Big O 표기 :O(log n),O(nlog n)
빅오 표현식 단순화하기
-
상수 무시하기
상수는 전반적인 추세에 큰 영향을 미치지 않기 때문에 무시한다.
O(2n) -> O(n)
O(500) -> O(1)
O(13* n^2) -> O(n^2) -
작은 연산 무시하기
작은 연산 또한 값에 큰 영향을 미치지 않기 때문에 무시한다.
O(n + 10) -> O(n)
O(1000n +50) -> O(n)
O(n^2 + 5n +8) -> O(n^2)
Bio O Notation을 이용해 시간 복잡도와 공간 복잡도를 분석할 수 있다.
시간 복잡도: 입력값의 증가에 따른 "실행 속도"의 변화
공간 복잡도: 입력값의 증가에 따른 "사용되는 메모리"의 변화
시간 복잡도 계산하기
- 산수는 상수다. (덧셈,뺄셈,곱셈,나눗셈)
작은 수와 큰 수를 연산하는데 걸리는 시간은 비슷하다.
ex. 2+2와 100000+2를 처리하는 시간은 비슷하다. - 변수 할당은 상수다.
컴퓨터가 변수에 값을 배정하는데 걸리는 시간은 비슷하다.
ex. x에 100을 할당하는 것과 20000을 할당하는데 걸리는 시간은 비슷하다. - 인덱스를 이용해서 배열에 있는 요소에 접근하는 것은 상수다.(object도 마찬가지)
배열에서 첫번째 아이템을 찾는 것과 10번째 아이템을 찾는 것은 비슷한 시간이 걸린다. - 루프가 있으면 시간 복잡도는
(루프 길이) x (루프 안에 있는 연산의 개수)이다.
공간 복잡도 계산하기
- 대부분의 primitive(undefined, null, numbers, booleans)들은 불변 공간(constant space)이라고 여긴다.
입력값의 크기와는 상관 없이 같은 공간을 차지함. -> O(1) - string은 O(n)만큼의 공간을 차지함.(이때, n은 문자열의 길이를 뜻함.)
- Reference type(array, object)들은 일반적으로 O(n)만큼의 공간을 차지함.(이때, n은 배열의 크기나 객체의 key의 개수를 의미한다.)
📌 퀴즈
- 시간 복잡도


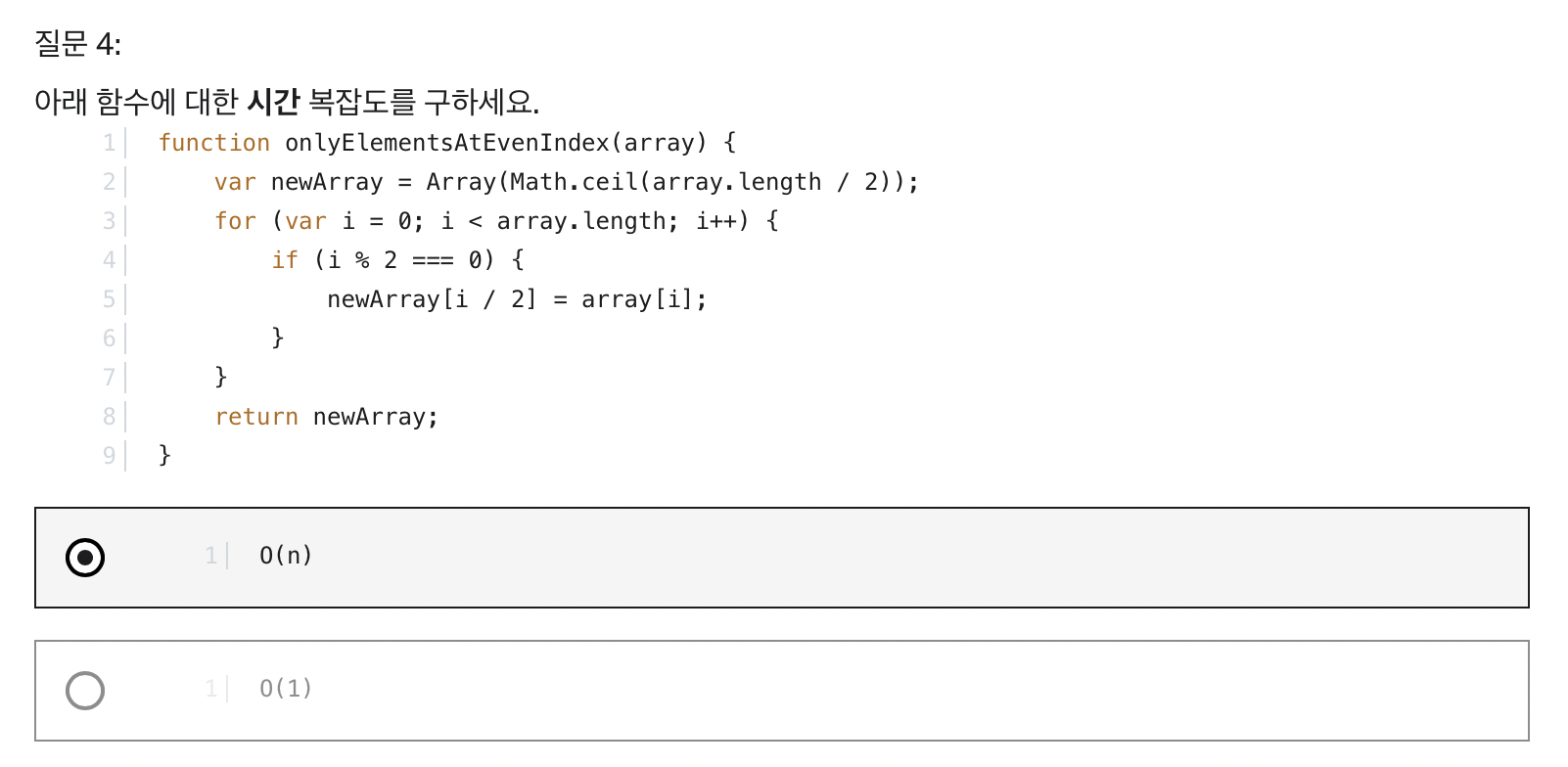
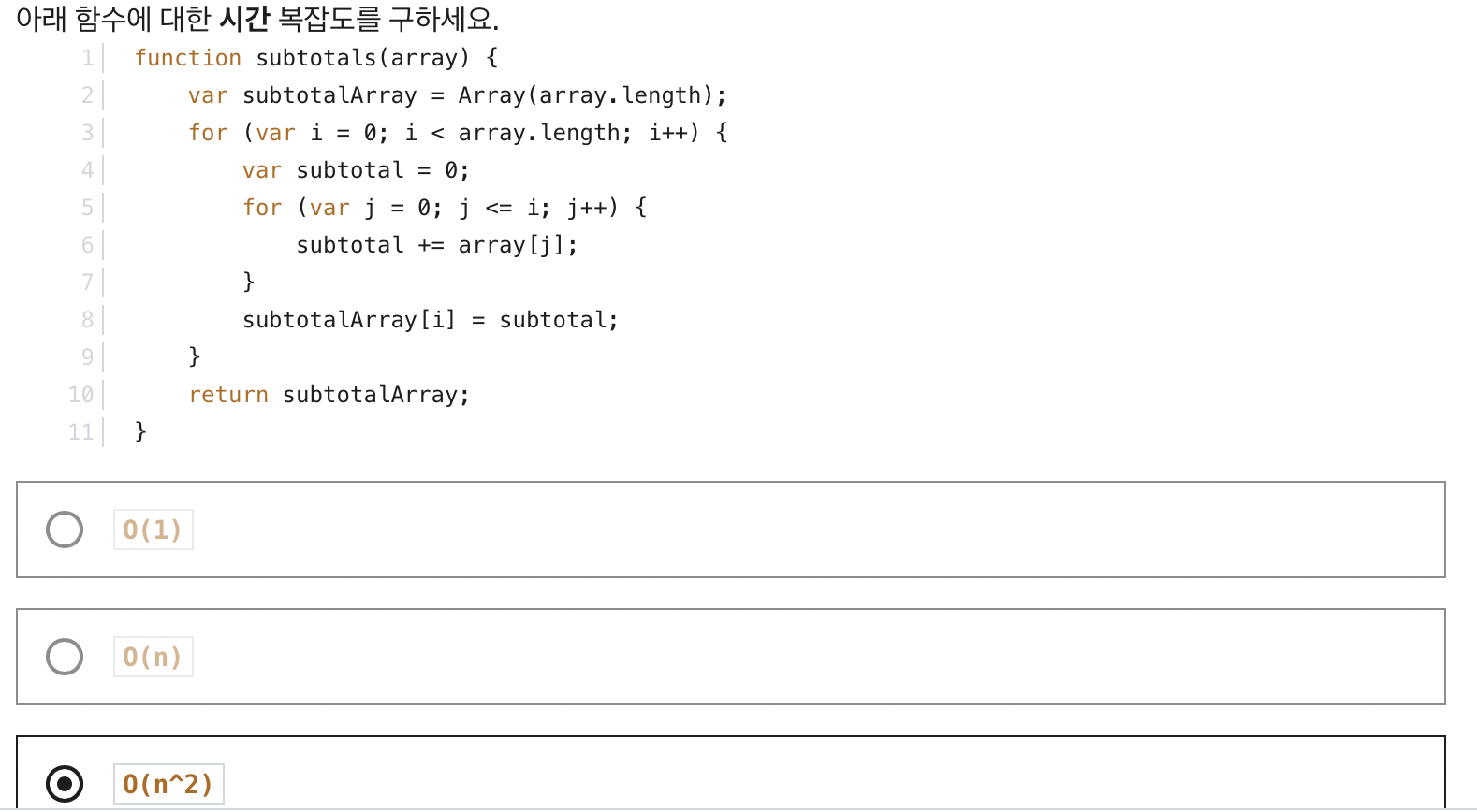
- 공간 복잡도

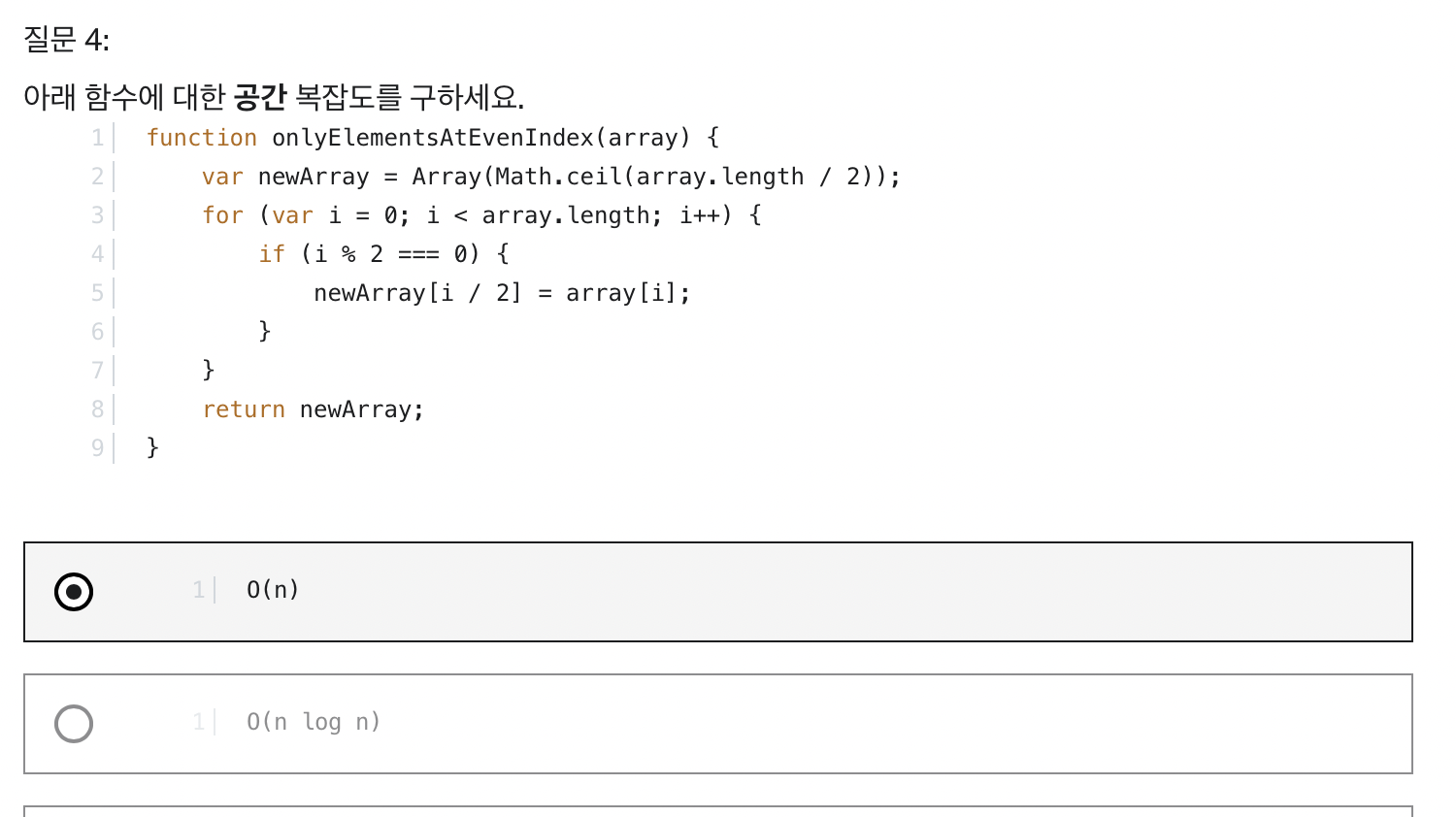

Logarithms
O(1), O(n), O(n^2) 보다 복잡한 문제들이 나올 수도 있는데 그중 하나가 로그이다.
탐색 알고리즘, 효율적인 정렬 알고리즘, 재귀와 연관되어 있다.
로그 시간 복잡도
O(log n)
처음에 조금 가파르다가 서서히 경사가 작아짐.
시간 복잡도가 O(1) 보다는 안좋고 O(n) 보다는 좋다.O(nlog n)
시간 복잡도가 O(n) 보다는 안좋고 O(n^2) 보다는 좋다.
Big O Notation 내용 요약
- 알고리즘의 performance를 분석할 수 있다.
- 시간/공간 복잡도에 대한 이해를 높일 수 있다.
- 정확도가 아니라 전반적인 추세를 중요하게 생각한다.
- Big O로 측정되는 알고리즘의 시간과 공간 복잡도는 하드웨어에 영향을 받지 않는다.
참고
코드 간편하게 실행할 수 있는 도구로 snippets 활용하기
크롬 개발자 도구 -> sources -> snippets
