📌 Tree
노드들이 부모/자식 관계로 이루어진 자료구조.
앞에서 배운 리스트들은 선형구조(linear) 이지만, 트리는 비선형구조(nonlinear)이다.
용어
- Root : 트리 꼭대기에 있는 노드
- Child : 다른 노드와 연결되어 루트로부터 멀어지는 노드
- Parent : child의 반대 개념
- Siblings : 같은 부모를 가진 노드들
- Leaf : 자식이 없는 노드(말단)
- Edge: 한 노드에서 다른 노드로 향하는 화살표
예시
HTML DOM
Network Routing
Abstract syntax tree
AI
Folders in Operating system
Computer file system
Tree 종류
아래의 것들 이외에도 매우 다양한 종류의 트리가 존재한다.
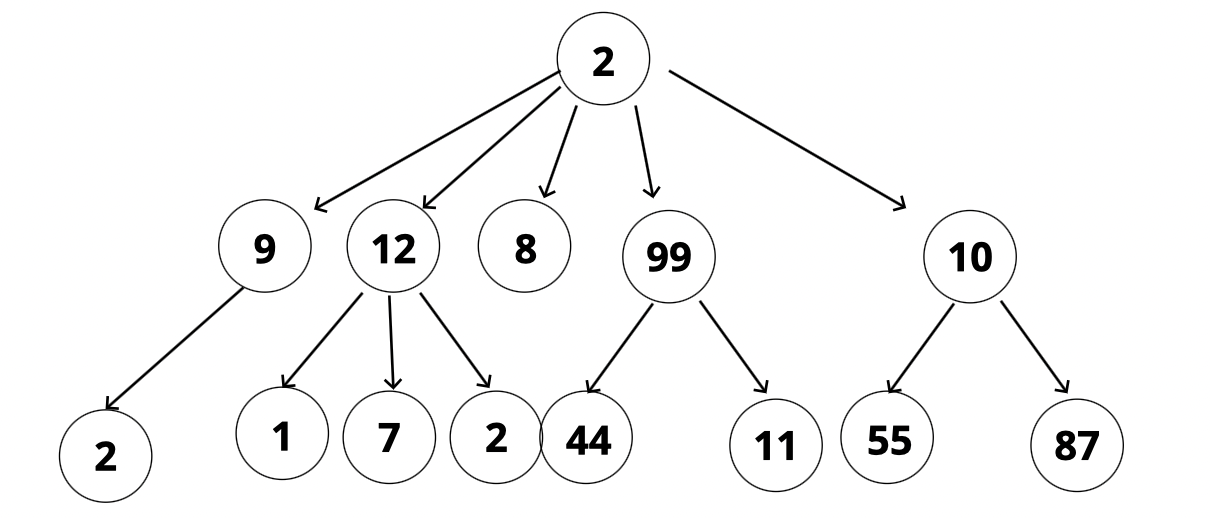
- trees (기본 트리) : 노드 수에 정해진 규칙이 없음.
- binary trees (이진 트리) : 각 노드가 최대 2개의 자식을 가질 수 있음.
- binary search trees(BST) (이진 탐색 트리) : 이진 트리 + 데이터를 정렬해서 비교 가능하게 저장함.
📌 binary search trees(BST) 특징
- 각 부모는 최대 2개의 자식 노드를 가질 수 있다.
- 부모 노드의 왼쪽에 있는 모든 노드는 언제나 부모보다 작다.
- 부모 노드의 오른쪽에 있는 모든 노드는 언제나 부모보다 크다.
- 이진 탐색 트리는 기본적인 트리에 비해 탐색이 훨씬 빠르다.
Q. 유효한 BST인가?
정답 : 아니다. 8의 오른쪽 자식 노드가 8보다 커야 하는데 더 작기 때문이다.
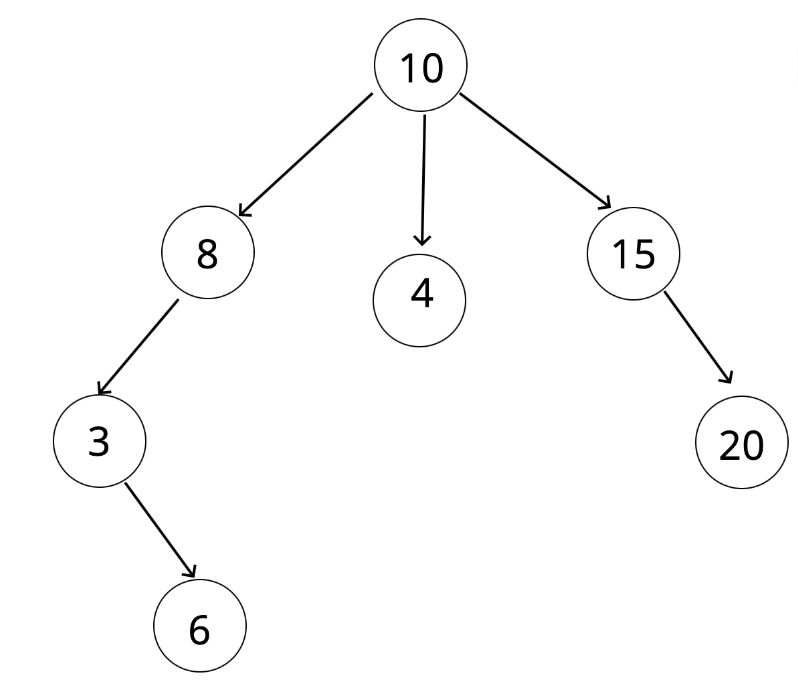
정답 : 아니다. 자식 노드 수가 최대 2개여야 하는데 10의 자식 노드가 3개 이므로 이진 트리가 될 수 없다.
트리 클래스 구현
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
}
// 10
// 7 15
// 9
var tree = new BinarySearchTree();
tree.root = new Node(10);
tree.root.right = new Node(15);
tree.root.left = new Node(7);
tree.root.left.right = new Node(9);메소드 구현
1. insert( )
적절한 위치에 값을 넣어주는 메소드.
순환식/재귀식 중 선택해서 풀면 된다.
- 루트가 있는지 확인 -> 없으면 해당 값을 루트로 설정
- 루트가 있는 경우, 루트와 대소관계를 비교하여 작으면 왼쪽 노드가 존재하는지 확인 -> 없으면 해당 값을 왼쪽 값으로 설정. 있으면 다시 대소관계 비교.(반복)
- 루트보다 크면 오른쪽 노드가 존재하는지 확인 -> 없으면 해당 값을 오른쪽 값으로 설정. 있으면 다시 대소관계 비교.(반복)
- 일치하는 경우는 undefined를 출력해도 되고, 갯수를 세주어도 된다.
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
var newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
var current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
}
// 10
// 5 13
// 2 7 11 16
var tree = new BinarySearchTree();
tree.insert(10)
tree.insert(5)
tree.insert(13)
tree.insert(11)
tree.insert(2)
tree.insert(16)
tree.insert(7)2. find( )
트리에 해당 값이 존재하는지 확인(해당 값 출력)
+contains( ) : 트리에 해당 값이 존재하는지 확인(T/F 출력)
- 루트가 없으면 false를 출력.
- 노드 끝에 도달할 때까지 or 해당 값을 찾을 때까지 이동.
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
var newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
var current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
find(value){
if(this.root === null) return false;
var current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
found = true;
}
}
if(!found) return undefined;
return current;
}
contains(value){
if(this.root === null) return false;
var current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
return true;
}
}
return false;
}
}
⭐️ 이진 탐색 트리 Big O
평균적인 & 최고의 경우,
삽입 & 탐색 : O(log n)
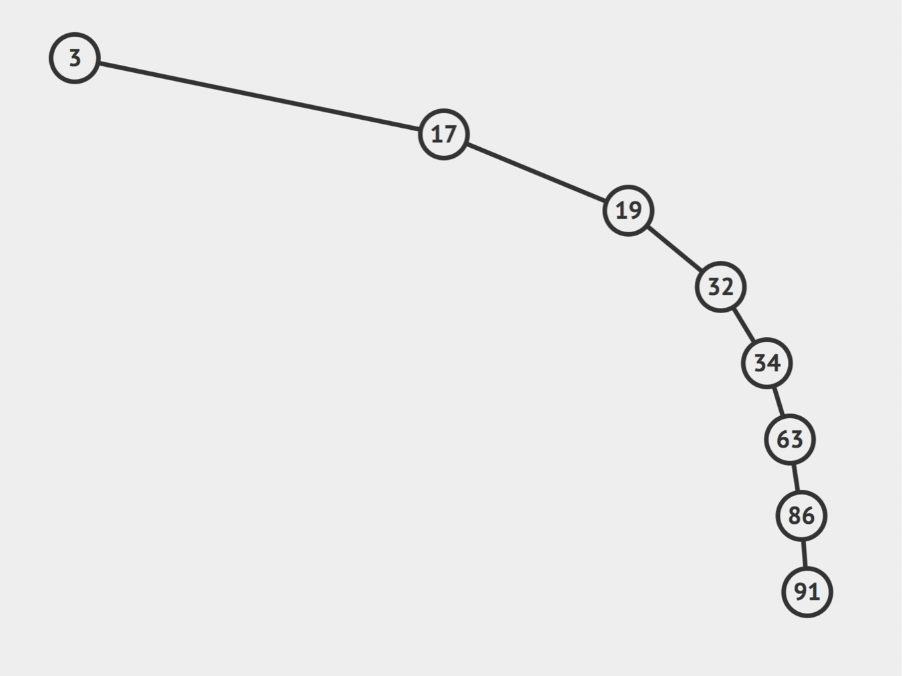
최악의 경우 : 연결 리스트 형태로 되어있는 트리의 경우
해결책 : 트리를 안쓰면 된다.