합병 정렬

🔗 합병 정렬, 퀵 정렬, 지수 정렬

• 매우 빠른 정렬 방법이다.
• 시간 복잡도를 O(n^2)에서 O(n log n)로 향상시킬 수 있다.
  앞에서 배운 세 가지 정렬 방식보다 빠르다.
• 효율성이 높지만, 이해하기 어렵고 가독성이 좋지 않다.

📌 합병 정렬(Merge Sort)

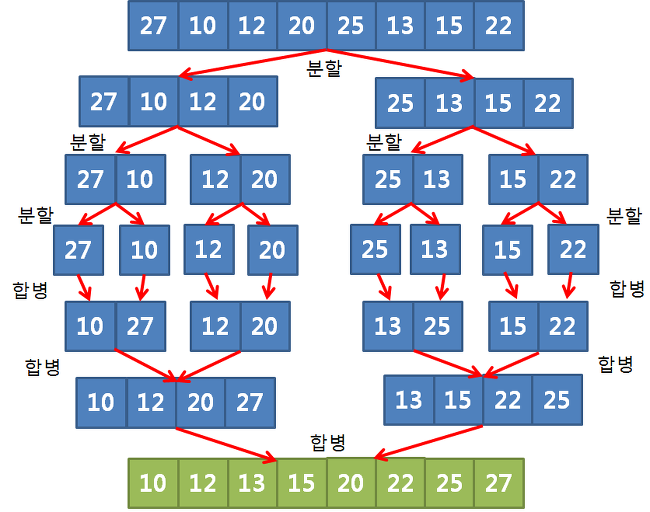
배열을 계속 반으로 나눠서 단일 배열로 분할한 뒤, 다시 정렬하면서 병합한다. => 분할 정복 알고리즘

ex. n개의 element가 담긴 배열이 있으면, n개의 단일 요소 배열이 될 때까지 계속 반으로 분할하고 다시 정렬하면서 병합시킨다.

대부분의 합병 정렬 구현 시 재귀를 사용한다.

합병 정렬 과정 애니메이션으로 보기
https://visualgo.net/en/sorting?slide=1-1

두 개의 정렬된 배열을 병합하는 방법

1. 병합한 값을 담을 새로운 배열을 하나 만든다.

let answer = [];

2. 두 개의 정렬된 배열에 각각 index를 설정한다. (i = 0, j = 0)

[1,10,50], [2,14,99,100]
 i          j

3. 맨 앞에서부터 값을 비교하며 더 작은 값을 새로운 배열에 순서대로 담는다.

[1,10,50], [2,14,99,100]
 1->3->5    2->4
answer = [1,2,10,50]

4. 한 배열의 끝에 도달하면, 다른 배열의 남은 값을 모두 취해준다.
   (더 이상 비교할 필요가 없기 때문.)

[1,10,50], [2,14,99,100]
				(전부 넣기)
answer = [1,2,10,50,99,100]

두 개의 정렬된 배열 병합 구현하기

// Merges two already sorted arrays
function merge(arr1, arr2){
    let results = [];
    let i = 0;
    let j = 0;
    while(i < arr1.length && j < arr2.length){
        if(arr2[j] > arr1[i]){
            results.push(arr1[i]);
            i++;
        } else {
            results.push(arr2[j])
            j++;
        }
    }
    // 한 배열의 끝에 도달한 경우
    while(i < arr1.length) {
        results.push(arr1[i])
        i++;
    }
    while(j < arr2.length) {
        results.push(arr2[j])
        j++;
    }
    return results;
}
merge([100,200], [1,2,3,5,6])

⭐️ 합병 정렬 구현

point : 재귀를 이용한다.

mergeSort 함수

1. 중간 지점을 정한다.
2. 중간 지점을 기준으로 좌,우로 나누어 재귀와 slice()를 이용해 단일 배열이 될 때까지 반으로 계속 나눈다.

merge 함수

1. 배열 2개를 입력 받아서 정렬하며 병합한다.
   (위에서 구한 함수와 동일함.)

ex) [10,24,76,23]

step1. left = [10,24]  (mergeSort) 				
step2. left = [10]     (mergeSort) 	
step3. right = [24]    (mergeSort) 	
step4. [10,24] 		   (merge)
step5.							    right = [76,23]  (mergeSort) 	
step6. 								left = [76]      (mergeSort) 	
step7.							 	right = [23]     (mergeSort) 	
step8. 								[23, 76]  		 (merge)
step9. [10,23,24,76] (merge) 끝!

코드

// Merge function
function merge(arr1, arr2){
    let results = [];
    let i = 0;
    let j = 0;
    while(i < arr1.length && j < arr2.length){
        if(arr2[j] > arr1[i]){
            results.push(arr1[i]);
            i++;
        } else {
            results.push(arr2[j])
            j++;
        }
    }
    // 한 배열의 끝에 도달한 경우
    while(i < arr1.length) {
        results.push(arr1[i])
        i++;
    }
    while(j < arr2.length) {
        results.push(arr2[j])
        j++;
    }
    return results;
}
// Recrusive Merge Sort
function mergeSort(arr){
    if(arr.length <= 1) return arr;
    let mid = Math.floor(arr.length/2);
    let left = mergeSort(arr.slice(0,mid));
    let right = mergeSort(arr.slice(mid));
    return merge(left, right);
}

mergeSort([10,24,76,73])

⭐️합병 정렬의 Big O

시간 복잡도 : O(n log n)

• 평균,최고,최악의 케이스 모두 동일.
• 예외 케이스가 없고, 어떤 형태의 데이터가 주어지든 동일한 시간 복잡도를 보인다는 장점이 있음.

시간 복잡도가 n log n 으로 나타나는 이유

1. 분할 횟수

n개의 element가 담긴 배열이 주어질 때, 절반으로 계속 나눠서 단일 배열이 되게 하려면 총 log n만큼의 시행이 필요하다.

ex. [1,2,3,4,5,6,7,8]
  [1,2,3,4]    [5,6,7,8]
[1,2]  [3,4]  [5,6]  [7,8]
[1][2] [3][4] [5][6] [7][8]

=> 8개로 나누기 위해 3번의 실행이 필요. (반대로 2^3 = 8)

2. 합병 횟수

각 분할마다 합병할 때 n번씩 비교한다.
따라서 n x log n = n log n 이므로 시간 복잡도가 n log n이 된다.

공간 복잡도 : O(n)

공간 복잡도가 n으로 나타나는 이유

배열이 클수록 메모리에 더 많은 배열을 저장해야 한다.
공간 복잡도 측면에서는 버블 정렬, 선택 정렬, 삽입 정렬 보다 더 많은 공간을 차지한다.