Auto-Encoding Variational Bayes 논문 리뷰

박민수·2023년 8월 1일

Auto-Encoding Variational Bayes

Variational Auto Encoder, VAE 모델로 잘 알려져 있는 논문이다.

Method

이 논문은 특이하게도 Related works가 없다,, 대신 현재 문제 상황에 대해서 정확하게 짚고 넘어간다.

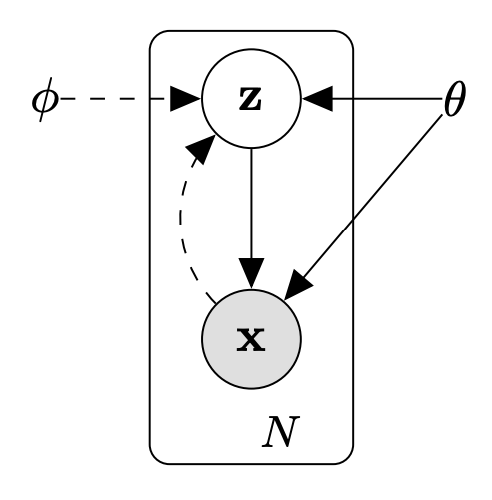
$x$ 는 데이터를, $z$ 는 $x$ 를 잘 설명할 수 있는 latent vector를 의미한다.
파라미터는 $\theta$ 와 $\phi$ 두 종류가 있는데, 이는 $z$ , $x$ 사이의 분포를 잘 설명하기 위해 우리가 학습시켜야 할 파라미터이다. 여기서 우리의 목표는 크게 두 가지가 있는데

첫 번째는 새 데이터를 생성하는 것이다. 논문에서는 생성에 필요한 파라미터를 $\theta$ 로 정리했고, $\theta$ 를 통해 추론한 $z$ 의 분포를 $p_{\theta}(z)$ , $z$ 가 주어졌을 때 $x$ 의 조건부 확률 분포를 $p_{\theta}(x|z)$ 라고 하면, $p_{\theta}(z)$ 분포를 따르는 latent vector를 sampling한 후 $p_{\theta}(x|z)$ 분포를 이용해 해당 latent vector에 맞는 적절한 $x$ 를 만들어낼 수 있다.

두 번째는 데이터로부터 latent vector를 잘 예측하는 것이다. 논문에서는 latent vector 예측에 필요한 파라미터를 $\phi$ 로 정리했다. 어떤 데이터가 들어오면 해당 데이터에 맞는 latent vector가 무엇인지 $q_{\phi}(z|x)$ 를 통해 예측해낼 수 있다.

결국 우리는 $p_{\theta}(z)$ , $p_{\theta}(x|z)$ , $q_{\phi}(z|x)$ 를 잘 학습시켜 실제 분포 $p_{\theta*}(z)$ , $p_{\theta*}(x|z)$ , $q_{\phi*}(z|x)$ 와 유사하게 만드는 것이 목표라고 할 수 있다. 그런데 $p_{\theta}(z)$ 는 우리가 잘 알고 있는 분포(본 논문의 VAE에서는 정규 분포)라고 가정해도 문제가 없고, 사실은 $p_{\theta}(x|z)$ 와 $q_{\phi}(z|x)$ 를 잘 학습하는 것이 목표이다.

Intractability?

그렇다면 $p_{\theta}(x|z)$ 와 $q_{\phi}(z|x)$ 를 잘 학습시키기 위해서는 어떻게 해야할까? MLE와 비슷한 접근법으로 $p_{\theta}(x)$ 를 높여야 한다는 것이 VAE의 접근이다. 그런데 $p_{\theta}(x)$ 는 앞서 살펴본 $p_{\theta}(z)$ , $p_{\theta}(x|z)$ 두 가지 값만으로는 계산이 사실상 불가능하다. $\int p_{\theta}(x|z) p_{\theta}(z) dz$ 로 계산할 수 있는 것처럼 보이지만, 모든 $z$ 에 대해 적분하는 것은 실제로 불가능한 일이기 때문이다. 이런 문제를 논문에서는 Intractability라고 이야기하고, Intractability를 해결하기 위해 아래의 variational bound를 사용한다.

The Variational Bound

$p_{\theta}(x)$ 의 정확한 값을 구하는 것이 목표는 아니고 값을 크게 만드는 것이 목적이기 때문에 $log(p_{\theta}(x))$ 의 값을 늘리면 된다고도 볼 수 있다. $log(p_{\theta}(x))$ 는 아래와 같이 표현할 수 있다.

$log\,p_{\theta}(x)=log\,p_{\theta}(x)\int q_{\phi}(z|x)dz$
$=\int log\,p_{\theta}(x)\, q_{\phi}(z|x)dz$

그런데 아래의 Bayes Rule

$p_{\theta}(x)=\frac{p_{\theta}(x|z)\,p_{\theta}(z)}{p_{\theta}(z|x)}$

을 위 식에 대입하면 (식이 복잡해 보이는데 하나씩 따라가면 어렵지 않아요 ㅜ)

$\int log\,p_{\theta}(x)\, q_{\phi}(z|x)dz=\int log(p_{\theta}(x|z)\,p_{\theta}(z)/p_{\theta}(z|x))q_{\phi}(z|x)dz$
$=\int log\, p_{\theta}(x|z)q_{\phi}(z|x)dz + \int log\, p_{\theta}(z)\,q_{\phi}(z|x)dz - \int log\, p_{\theta}(z|x)\,q_{\phi}(z|x)dz$
$=E_{q_{\phi}(z|x)}[log\, p_{\theta}(x|z)] + \int log\, p_{\theta}(z)\,q_{\phi}(z|x)dz - \int log\, p_{\theta}(z|x)\,q_{\phi}(z|x)dz$
$=E_{q_{\phi}(z|x)}[log\, p_{\theta}(x|z)] + \int log\, p_{\theta}(z)\,q_{\phi}(z|x)dz - \int log\, p_{\theta}(z|x)\,q_{\phi}(z|x)dz + \int q_{\phi}(z|x)log\,q_{\phi}(z|x)dz-\int q_{\phi}(z|x)log\,q_{\phi}(z|x)dz$
$=E_{q_{\phi}(z|x)}[log\, p_{\theta}(x|z)] + \int q_{\phi}(z|x)log\,\frac{q_{\phi}(z|x)}{p_{\theta}(z|x)}dz-\int q_{\phi} (z|x)log\,\frac{q_{\phi}(z|x)}{p_{\theta}(z)}dz$
$=E_{q_{\phi}(z|x)}[log\, p_{\theta}(x|z)] + D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x))-D_{KL}(q_{\phi}(z|x)||p_{\theta}(z))$

이고, 따라서

$log\,p_{\theta}(x)=E_{q_{\phi}(z|x)}[log\, p_{\theta}(x|z)] + D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x))-D_{KL}(q_{\phi}(z|x)||p_{\theta}(z))$

로 표현이 가능하다.
그런데 여기에서 KL Divergence가 0이상이라는 특징을 생각해 보면,

$D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x))$ 도 0 이상이기 때문에

$log\,p_{\theta}(x)\geq E_{q_{\phi}(z|x)}[log\, p_{\theta}(x|z)] -D_{KL}(q_{\phi}(z|x)||p_{\theta}(z))$

라고 할 수 있다. 그렇다면

$E_{q_{\phi}(z|x)}[log\, p_{\theta}(x|z)] -D_{KL}(q_{\phi}(z|x)||p_{\theta}(z))$ 만큼이 $log\,p_{\theta}(x)$ 의 lower bound 역할을 한다고 말할 수 있고, 따라서 $E_{q_{\phi}(z|x)}[log\, p_{\theta}(x|z)] -D_{KL}(q_{\phi}(z|x)||p_{\theta}(z))$ 를 최대로 만들어 $log\,p_{\theta}(x)$ 도 함께 최대에 가까워지게 만들 수 있다.

이러한 방식을 variational bound라고 말한다.

SGVB Estimator, AEVB Algorithm

본 논문에서는 Monte Carlo Method를 사용하여 학습을 진행하는 방향을 선택한다.
Monte Carlo Method는 여러 번의 시행(sampling)을 통해 실제 기댓값과 가까워지는 방법을 의미한다. 주사위를 정말 많이 던져서 1이 나올 확률(1이 나온 횟수/전체 횟수)를 계산한다면 점점 1/6에 가까워질 것이고, 이와 같은 방식으로 기댓값을 계산하는 방식이 Monte Carlo Method이다.

Monte Carlo Method를 likelihood 계산에 사용하기 위해 $E_{q_{\phi}(z|x)}[log\, p_{\theta}(x|z)] -D_{KL}(q_{\phi}(z|x)||p_{\theta}(z))$ 를 추정하기 위한 적당한 식을 만들고 그것을 SGVB(Stochastic Gradient Variational Bayes) estimator 라고 부르기로 하였다. 자세한 식은

$\displaystyle\tilde{L}(\theta,\,\phi,\,x^{(i)})=\frac{1}{L}\sum_{l=1}^{L}log\,p_{\theta}(x^{(i)},\,z^{(i,l)})-log\,q_{\phi}(z^{(i,l)}|x^{(i)})$
$where\;\;z^{(i,l)}=g_{\phi}(\epsilon^{(i,l)},x^{(i)})\;\;and\;\;\epsilon^{(l)}\sim p(\epsilon)$

이다.
식에서 L은 샘플링 횟수이고, $g$ 에 대한 설명은 Reparameterization trick에서 자세히 다룰 것이다.

이를 이용해 실제로 학습시키는 알고리즘은 AEVB라고 한다. 특별한 점은 없고, Sampling 횟수 L을 만들어 놓고 1로 사용했다는 점이 약간 어색하긴 하다.

Reparameterization trick

앞서 말했듯 Monte Carlo Method를 적용하기 위해 sampling을 여러 번 수행하게 되는데, sampling을 진행하게 되면 gradient가 흐르지 않는다는 치명적인 문제가 발생한다.
$z\sim q_{\phi}(z|x)$ 인 상황에서 어떤 $z$ 를 바로 샘플링하기 보다는 랜덤성이 부여될 수 있는 부분들을 미리 샘플링 해 놓고 그것들을 $\epsilon$ 이라고 부르면 $z$ 를