[Algorithm] 숫자 개수 세기

이진탐색을 활용해야 풀 수 있는 '숫자 개수 세기' 문제 분석 및 오답 노트

• 질문에 적혀있는 숫자가 실제로 주어진 숫자중에 몇개나 포함되어 있는지를 '세는' 문제
• 그러나, 간단하게 물어보는 숫자가 있는지를 알기 위해 리스트를 한번 쭉 탐색하는 방법은 리스트의 개수(N), 질문의 개수(M)이라할 때 결국 O(N*M)이 되어 O(N2)이되는데, 여기서 N,M 둘다 100,000이 최대이므로, N2을 하면 1억이 넘게돼서 시간 제한에 걸리게 된다. 여기서 좀 더 생각이 필요하게됨.
• 뭔가를 센다(count) 혹은 뭔가를 찾을 때(search), O(N)보다 빠른 시간복잡도를 가지는 탐색법은 '이진탐색(Binary Search)'법이 있음(logN의 시간복잡도).
• 하지만, 이진탐색은 먼저, 정렬이 돼야 쓸 수 있는 알고리즘이기에 신중해야하는데, 이 경우에는 O(NlogN)로 정렬을 먼저하고 이진탐색 (logN)의 시간복잡도로 질문의 개수만큼 수행하는 것(M x logN)이 훨씬 빠르다고 판단할 수 있음. 결론적으로 정렬을 먼저하고, 이진탐색으로 M개의 질문에 대해 탐색을 수행하면 O(NlogN) + NlogN)이므로 결론적으로 O(NlogN)으로 찾을 수 있음. O(N2)의 풀이에 비하면 월등히 나은 시간 복잡도임.

문제에 대한 설계 단계

• 그렇다면 이진탐색을 이용하는데, 어떻게 이용할 것인가 ??
• 개수를 세는 것이기 때문에 예를 들어, 1이 몇개인지 알려면(정렬된 리스트에서) 1보다 작은 것과 1 그리고 1보다 큰 것과 1의 '경계'를 찾아서 그 둘을 뺀 다음에 -1을 해주면 그 사이에 1의 개수를 얻을 수 있다.
• 결론적으로, 찾고자하는 수와 그보다 작은수 그리고 큰수와의 경계면을 이진탐색으로 찾으면 된다.
• 재귀함수를 이용하여 이진탐색을 구현해본다.
• 작은수와의 경계를 찾는 함수, 큰수와의 경계를 찾는 함수를 각각 만든다.
• 찾고자하는 값을 num이라하고, 매 콜스택마다(재귀함수의) 탐색할 범위를 s(start_idx), e(end_idx)로 둔다.
• 재귀함수 디자인
  • 재귀함수는 찾고자하는 값(num)과 그보다 작은수(큰수)와의 경계에 해당하는 요소의 인덱스를 리턴한다.
  • 기저조건으로는 만약 시작인덱스가 끝인덱스(s가 e보다)보다 크거나 같은 시점이 되면, 이중 if문으로 그 시점에서 만약 작은수를 찾는 경우에는 전체 배열의 인덱스0이 찾고자하는 값이면, 인덱스0부터 전부 찾고자하는 값일테니 0보다 작은 -1을 리턴하고, 만약 큰수를 찾는 함수의 경우에는 전체 배열의 인덱스 -1(맨 끝값)이 찾고자하는 값이면 전체 배열의 길이를 리턴한다(마지막 인덱스+1). 그리고 두 함수 모두 만약 앞서 말한 이중 if문에서의 조건이 False면 None을 리턴한다.
  ** 만약 [2,2,2,2,2,2,2,2,2]에서 경계면을 찾으려하면 사실상 경계가 없게된다. 이러한 경우에 대비해서 위의 이중 if문 조건을 준 것이다. 내가 짠 로직대로라면 이렇게 배열이 주어진 경우 전체 배열의 길이 n=9과 -1 이 각각 큰경계를 함수로와 작은경계를 찾는 함수로부터 리턴될 것이고 결과적으로 9-(-1)-1=9가 되므로, 2의 개수인 9개가 도출된다. 하지만, 인덱스0과 -1이 찾고자하는 값이 아니라면 None을 리턴하는 것은 이 배열에 2가 없는 경우일 것이다. ex) [0,0,0,0,0,1,1,1,1]
• 실제적인 재귀함수 로직(=이진탐색 로직)
  1. mid라는 변수에 정중앙 인덱스인 (s+e)//2의 값을 넣어준다.
  2. 그 다음에 세가지 경우로 분기처리하는데, 작은 경계를 찾는 부분만 써보면(큰경계를 찾는 부분은 그 반대이기에), 첫번째 조건으로, 중간에 해당하는 인덱스의 요소가 찾고자하는 값인 num보다 작으면, 또다시 2개의 조건으로 분기할 수 있는데, 이 떄, mid+1 인덱스에 해당하는 요소가 num이면 예를 들어, 1,2를 나란히 찾았는데 2가 찾고자 했던 값이라면 1에 해당되는 인덱스가 찾고자했던 경계일 것이므로, mid를 리턴한다. 하지만, 찾고자하는 값이 아니라면 mid+1부터 e까지 다시 재귀함수를 콜스택에 쌓는다.
  3. 두번째 조건으로 mid에 해당하는 요소가 num보다 클경우에는 작은 경계를 찾는 함수이기에 그 위는 볼필요가 없으므로 바로 재귀함수를 다시 돌린다. 이 때 s,e 중에 e=mid-1로 고쳐서 돌린다.
  4. 마지막으로, mid에 해당하는 요소가 num, 즉, 찾고자하는 값과 일치했을 때는, 또 이중if문을 써야하는데, 같으면서 mid-1에 해당하는 요소가 num보다 작은경우에는 그 인덱스가 경계가 되므로, mid-1을 리턴해준다. 하지만, 그렇지 않은 경우에는 또다시 e=mid-1을 해준다음에 재귀함수를 쌓는다.
  5. 큰경계를 찾는 함수도 이와 유사하지만, 반대의 로직으로 만들고 난 다음에, 실제로 질문에 따라 개수를 서치할 때는 만약 작은 경계에서 None이 나오면 실제로 이 배열에는 해당 값이 없는 것이기에 큰 경계를 찾는 함수를 아예 돌리지 않아도 된다.
  6. 여태까지가 문제에 대한 설계이다.

  ---

실제 구현 코드(by python)

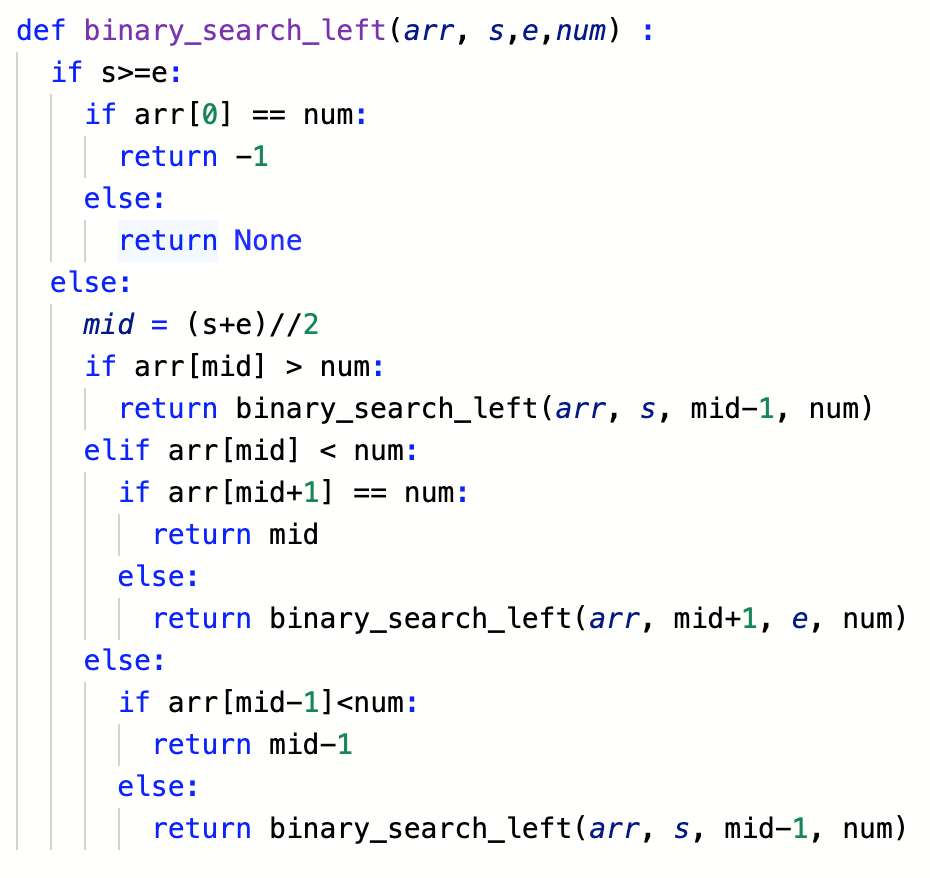
1) 작은 경계를 찾는 함수

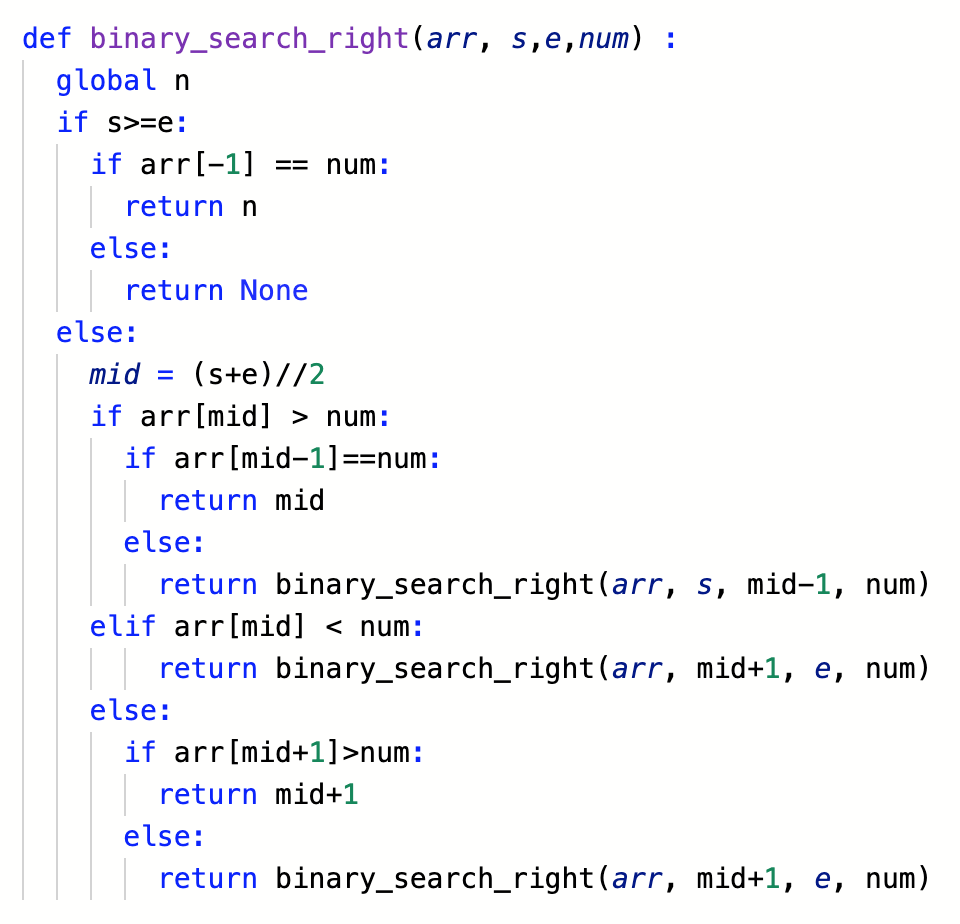
2) 큰 경계를 찾는 함수

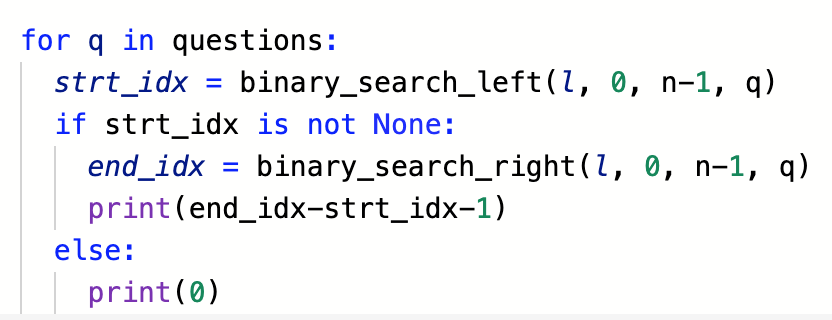
3) 실제로 질문을 받아서 서치하고, 개수를 리턴하는 부분

오답 포인트

• 처음에 이문제에서 헤맸던 것은 '[2,2,2,2,2,2]'와 같은 케이스를 대비하지 못했기 때문이다.
• 그래서 처음에는 이진탐색으로 경계를 찾지 않고, 단순히 이진탐색으로 만약 2를 찾고자 했다면, 2를 찾고, 그 다음에 양옆으로 while문을 써서 2를 카운트하고 끝내는 함수를 썼다. 하지만, 위 경우처럼 전부 2로된 케이스면, 결국 한번의 시행에 O(N)+O(logN)이 되므로 결국 O(N)이 되는데, 이러면 처음에 생각한대로 최종 시간 복잡도는 O(N2)돼서 오답이됐다..
• 이진탐색을 반드시 특정 수를 찾는데에만 국한해서 쓰지말고, 이 경우처럼 너무 많은 경우를 탐색할 때, 정렬을 한채로 반씩 쪼개서 볼 수 있다는 접근으로 활용하는 것이 좋을 것 같다. 불확실한 문제에서 필요한건 상수와 같이 '확실한 뭔가'이다. 이 문제의 경우 그 '확실한 무언가'가 정렬이 된 상태에서 작은 것과 찾는 값, 찾는 값과 큰 값간에 경계가 있다는 것이다.