1) 유클리드 호제법
=> 최대 공약수와 최소 공배수(최소공배수=구하려는 두개의 수의 곱/최대공약수)와 연관된 이론!
먼저,
최대공약수 및 최소공배수 관련 문제

출처 : 한국정보올림피아드 지역본선 2004 중등부 1번, 고등부 1번
이 문제를 유클리드 호제법이 아닌 방법으로 구현해보면,

이렇게 풀어볼 수 있다.
여기서 최대 공약수를 구한 방법은
1부터 차례대로 나눠보는 식이다. 1부터 차례대로 두 수의 나눠보면서 둘다 나눠떨어지는 수는
공약수일 것이고, 끝까지 탐색했을 때 가장 최근에 변수에 들어간 공약수가 최대공약수가 될 것이다.
이처럼 사실 최대공약수를 구하는 것은 그렇게 어렵지 않다(유클리드 호제법을 안써도)
예를 들어, 6 18의 최대공약수를 구해보면
각각에 2를 나눠보고, 3을 나눠보면 더이상 나눌 수 없기 때문에 (공약수로)
2*3 = 6이 최대공약수가 된다.
그러나, 이러한 과정을 유클리드 호제법을 통해 구해보면 더욱 간단해진다.
a,b,r 이 있을 때 a,b는 최대공약수를 구하려는 두수가 되고(a>b),r은 a에서 b를 나눈 나머지가 된다.
그럼 이경우에는 18,6, 0이 되는데,
유클리드 호제법은
a b r
18, 6, 0
이런식으로 a에서 b를 나눈 나머지를 r로하고, 만약 r이 0이면
b가 최대공약수가 되는 규칙을 이용한다.
이 경우는 한번에 r이 0으로 나온 경우이므로 다른 경우를 예로 들면
a b r
18 5 3
5 3 2
3 2 1
2 1 0
..ㅎㅎㅎ 아주 원시적으로 포스팅을 해서.. 모양이 들쑥날쑥인데 어쨌든
위를 보면 끝에 r이 0이되는 지점에서의 b가 1인 것을 통해 이 둘의 최대공약수가 1임을 알 수 있다.
그리고 그 과정을 보면 첫 번 째 케이스와 달리 r=0이 되기까지의 과정이 좀 더 길다.
이 때 첫 시행 이후 b의 값이 다음 a값이 되고, r값이 다음 b값이 됨을 볼 수 있다.
이런식으로 이전의 b값은 다음 a값이 되고, 이전 r값은 다음 b값이 되도록 한후 다시 a에서 b를 나눠 r값을 구하고,
그 r값이 0이될 때까지 같은 패턴을 반복하여 최대공약수를 구해내는 것이 유클리드호제법이다.
관련 문제 풀어보기

출처 :https://programmers.co.kr/learn/courses/30/lessons/12953?language=javascript
최소공배수 문제지만, 최소공배수 = 구하려는 두 수의 곱 / 최대공약수로 구할 수 있기 때문에 풀어봤다.
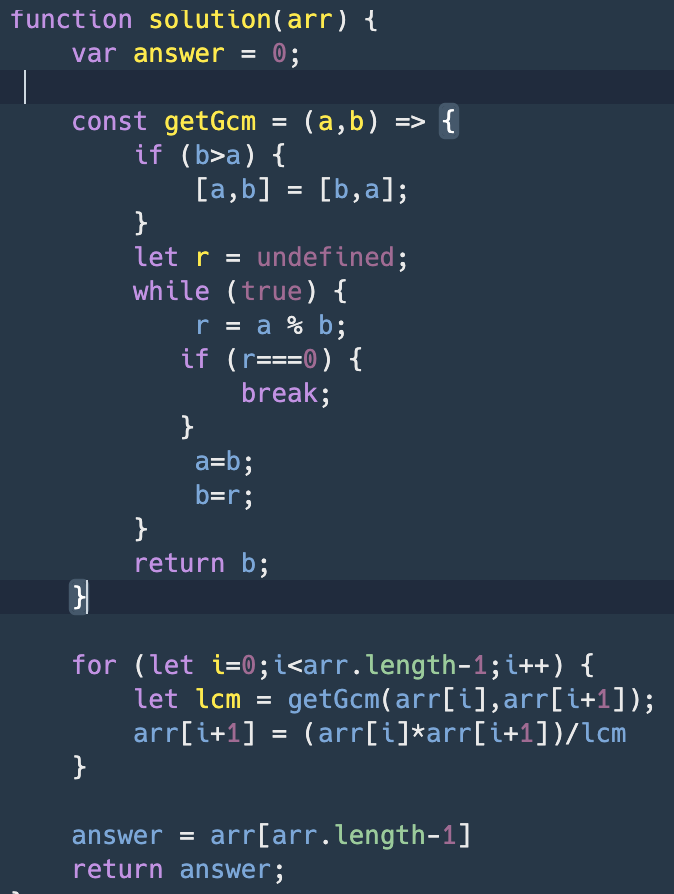
가운데에 getGcm이 최대공약수를 구하는 함수고, 유클리드 호제법을 이용했다.

그리고 이 부분에서 '최소공배수 = 구하려는 두 수의 곱 / 최대공약수' 이 공식을 이용했다.
사실 최대공약수를 구할 때는
1부터 시작해서 구하려는 두 수에 하나씩 나눠보면서 둘다 나눠떨어지는 순간에
최대공약수 변수에 그 공약수를 넣어주면서 전체를 순회하면 된다(이 때, 둘 중에 작은 값까지만 나눠보면됨)
근데, 문제는 이걸 시간복잡도 측면에서 생각해보면,
예를 들어, 10억이랑 999999999.. 극단적이지만..ㅎ의 최대공약수를 구하라했을 때,
만약 후자의 방법이면, 둘 중에 작은 값인 구억구천구백구십구번의 시행을 통해 최대공약수를 구할 수 있을 것이다.
그러나, 유클리드 호제법을 쓰면
a b r
10억 999999999 1
999999999 1 0
결국 최대공약수는 두번만에 1이라는 것을 알 수 있다.
둘다 O(n)의 시간복잡도를 가진다고 할 수 있지만..
실질적인 차이는 어마어마하다..
2)
에라토스테네스의 체
이에 대해서 살펴보기 전에 간단하게 개별 수에 대해서 소수인지 아닌지를 판별하는 함수를 만들어보면,
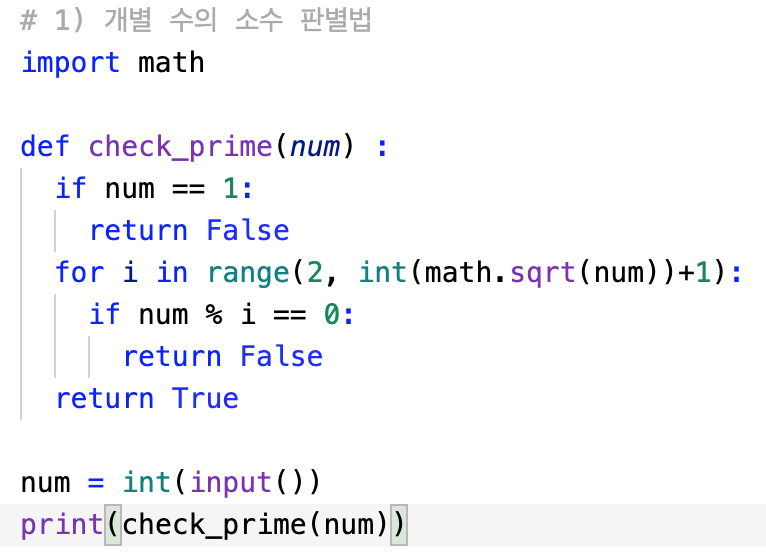
이렇게 된다.
간단하게 5가 소수인지 판별해보려면
2부터 5의 제곱근까지의 수를 5로 나눠봐서 나머지가 0인 것이 하나도 없으면 5는 소수라고 할 수 있다.
즉, 5제곱근까지 5의 약수가 안나타난다면!
5의 제곱근은 2.xxxxxx이기에 2까지만 나눠봐도 알 수 있다.
또다른 예로 25는
2,3,4,5까지 나눠보면
5가 25의 약수가 되므로 소수가 될 수 없다.
이 때, 제곱근까지 나눠보는 이유는 약수는 좌우 대칭의 성질을 띄기 때문에
굳이 남은 대칭까지 해볼 필요가 없는 것.
어쨌든 위의 방법은 개별 수의 소수 판별에 유용한 함수라고 할 수 있다.
그렇다면 에라토스테네스의 체는 언제쓰면 좋을까??.
에라토스테네스의 체가 유용한 부분은
1- 특정수(N)까지의 소수를 모두 찾는 부분이다.
처음 방법으로 위를 실현하려면
2부터(1은 소수가 아니므로) N까지 모든 수에 대해서 위의 함수(O(N))를 적용해보는 수밖에 없다.
하지만 에라토스테네스의 체를 이용하면 더욱 효율적으로 위를 실현할 수 있다.
그래서 에라토스테네스의 체는 뭔가하면
먼저, 2부터 기준점을 잡고 시작하는데, 기준점으로 잡은 수는 지우지 않고,
예를 들어, 1-50까지의 수중에 소수를 찾고 싶다했을 때,
50까지의 모든 2의 배수 혹은 2를 약수로 갖는 수를 지워준다.
그리고 그 다음 시행으로 3을 기준점으로 잡고
똑같이 기준점인 3은 지우지 않고, 모든 3의배수 혹은 3을 약수로하는 수를 지운다.
이런식으로 나아가다보면, 예를 들어, 4는 이미 2에서 지워졌기에 기준점이 되지 않고, 넘어가게되고,
5를 기준점으로 삼고, 또 같은 시행을 반복하며 나아간다.
그러다보면 2-50 의 범위에는 49개의 수가 있지만, 결국 49번의 시행 이전에 기준점으로 삼는 수가 점점 줄어들게 되고,
50까지 닿게 된다(물론 50은 2에서 이미 지워졌기에 기준점이 되지는 않을 것).
실제 코드로 구현해보면

이렇게 된다.
** 에라토스테네스의 체를 쓸 때도 제곱근까지만 구해봐도 결과를 명확히 알 수 있다.

실제로 50을 넣어보면
그사이의 소수를 모두 잘 판별함을 볼 수 있다.
두 개의 소수판별 알고리즘은 각각 유용한 시점에 적절히 쓰면 될 것 같다.
위의 경우처럼 범위 내에 모든 소수를 출력하라는 문제에서는 에라토스테네스의 체가 효율적인 것이 명확하고,
개별 수의 소수여부를 판별하는 부분에서는 전자의 알고리즘이 효율적일 것.
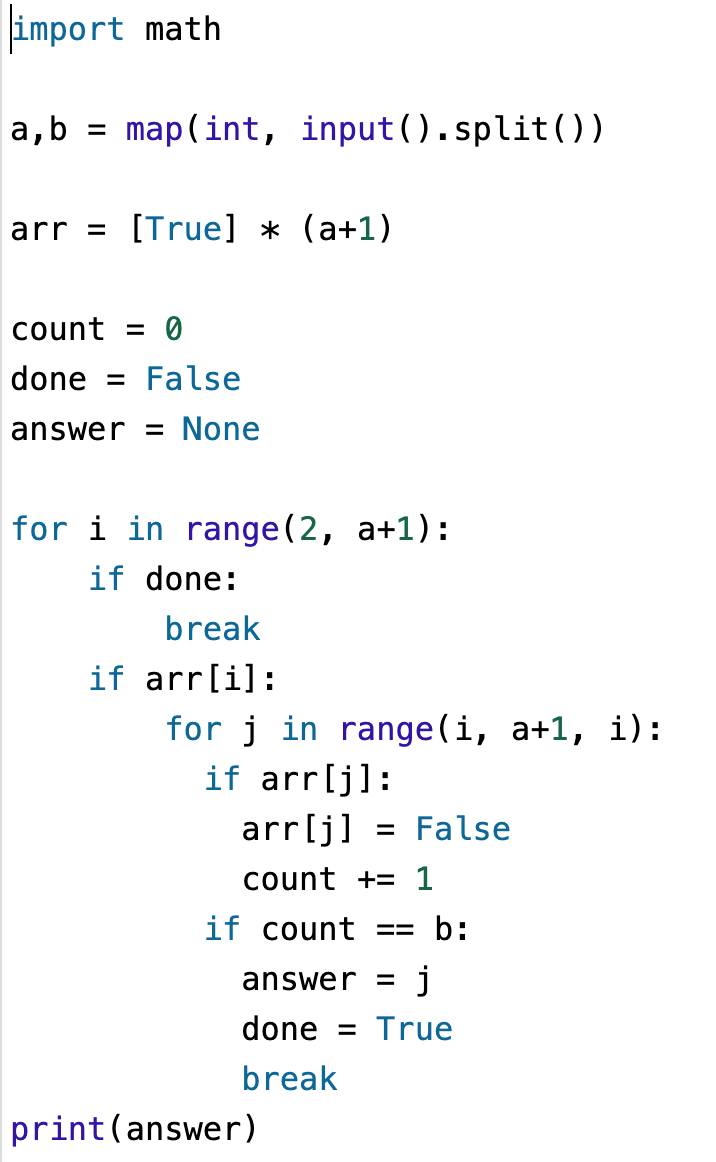
관련 문제 풀이
문제 :

출처 : 백준 알고리즘(https://www.acmicpc.net/problem/2960)
문제 풀이 :