BOJ 1707 이분 그래프

땡칠·2022년 1월 3일

bipartite graph ps

알고리즘

목록 보기

9/16

문제

도입

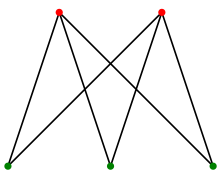
그래프 이론에서, 이분 그래프(二分graph, 영어: bipartite graph)란 모든 꼭짓점을 빨강과 파랑으로 색칠하되, 모든 변이 빨강과 파랑 꼭짓점을 포함하도록 색칠할 수 있는 그래프이다.

문제를 푸려다가 문제에 나와있는 말만으로는 이해가 잘 안되어 찾아봤다.
저건 성질에 더 가까운 것 같고 정의는 다음과 같다.

정의

설명

아이디어는 간단하다.
정점을 두 그룹으로 만들었을 때, 그룹 내에서 간선이 없게 하면 된다. 말 그대로 bipartite graph 이다.

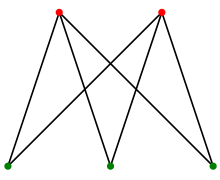
예시를 보면, 적색/초록 점끼리는 연결이 안되어있다.
정의에 따르면, 이것이 가능한 grouping 방법이 하나라도 존재하면 이분 그래프가 되는 것이다.

적용

그렇다면 어떻게 프로그램으로 구현할 수 있을까?
BFS, DFS등 탐색을 하며, 만나는 놈들마다 이웃한 정점과 반대의 색을 칠하자.
만약 탐색 중에 색이 칠해진 놈을 만났는데, 칠할 색과 반대다? 그렇다면 정의에 대해 모순이다.
따라서 해당 그래프는 이분 그래프가 아니다.
이런 판별 방법으로 구현하면 되겠다.

코드

// 2021.12.29 22:50:44
// 1707 https://boj.kr/1707
#include <bits/stdc++.h>
using namespace std;
#define RED 1
#define GREEN 2
#define VERTEX_MAX 20'001
#define EDGE_MAX 200'001

vector<vector<int>> edges(EDGE_MAX, vector<int>());
int visited[VERTEX_MAX];

int invertColor(int color)
{
    return color == RED ? GREEN : RED;
}

bool dfs(int vertex, int color)
{
    visited[vertex] = color;

    for (int next : edges[vertex])
    {
        if (visited[next] == color)
            return false;
        if (!visited[next] && !dfs(next, invertColor(color)))
            return false;
    }
    return true;
}

void init()
{
    for (int i = 1; i < EDGE_MAX; i++)
        edges[i].clear();
    for (int i = 1; i < VERTEX_MAX; i++)
        visited[i] = 0;
}

int main()
{
    cin.tie(0);
    ios::sync_with_stdio(false);
    int k;
    cin >> k;
    while (k--)
    {
        int v, e;
        cin >> v >> e;

        init();
        for (int i = 0; i < e; i++)
        {
            int v1, v2;
            cin >> v1 >> v2;
            edges[v1].push_back(v2);
            edges[v2].push_back(v1);
        }
        bool ret = true;
        for (int i = 1; i <= v; i++)
        {
            if (!visited[i] && !(ret = dfs(i, RED)))
                break;
        }
        cout << (ret ? "YES" : "NO") << '\n';
    }
}